Метод критического пути

Для расчета сетевого графика применяют разные методы. Одним из них является метод критического пути, который используется для управления проектами с фиксированным временем выполнения работ. Он позволяет ответить на следующие вопросы:

1. Сколько времени потребуется на выполнение всего проекта?

2. В какое время должны начинаться и заканчиваться отдельные работы?

3. Какие работы являются критическими и должны быть выполнены в точно определенное графиком время, чтобы не сорвать установленные сроки выполнения проекта в целом.

4. На какое время можно отложить выполнение некритических работ, чтобы они не повлияли на сроки выполнения проекта?

Все события и работы критического пути называются критическими. Продолжительность критического пути и определяет срок выполнения проекта. Критических путей на сетевом графике может быть несколько.

Для событий рассчитывают три характеристики: ранний и поздний срок совершения события, а также его резерв.

Обозначим t(i,j) - продолжительность работы с начальным событием i и конечным событием j.

Ранний срок t_p(j) свершения события j – это самый ранний момент, к которому завершаются все работы, предшествующие этому событию. Он определяется величиной наиболее длительного отрезка пути от исходного до рассматриваемого события, причем t _p (1) = 0, a t_p (N) = t_Kp (L):

t_p(j). = max { t_p(i) + t(i,j) }

где максимум берется по всем событиям i, непосредственно предшествующим событию j (соединены стрелками).

Поздний срок t_n (i) свершения события i – это такой предельный момент, после которого остается ровно столько времени, сколько необходимо для выполнения всех работ, следующих за этим событием. Характеризует самый поздний допустимый срок, к которому должно совершиться событие, не вызывая при этом срыва срока свершения ко­нечного события:

t_n(i) = min { t_n(j) – t(i,j) }

где минимум берется по всем событиям j, непосредственно следующим за событием i.

Этот показатель определяется «обратным ходом», начиная с завершающего события, с учетом соотношения t_п (N) = t_p (N).

Все события, за исключением событий, принадлежащих критическому пути, имеют резерв R(i):

Резерв R(i) события i показывает, на какой предельно допустимый срок можно задержать наступление этого события i, без нарушения срока наступления завершающего события:

код

R(i) = t_n(i) – t_p(i)

Критические события резервов не имеют.

tп

При расчетах круг, изображающий событие,

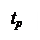
делят на 4 части

	R

Пример.

Рассмотрим сеть проекта, представленную следующими данными.

Работа	1-2	1-3	2-4	2-5	3-4	4-5	4-6	5-7
Продолжительность, нед

Найти критический путь. Сколько времени потребуется для завершения проекта? Можно ли отложить выполнение работы (2,4) без отсрочки завершения проекта в целом?? На сколько недель можно отложить выполнение работы (2,5) без отсрочки проекта в целом?

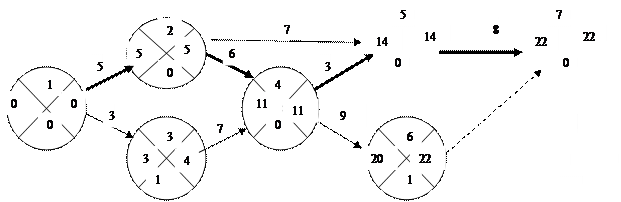
Рисуем сетевой график.

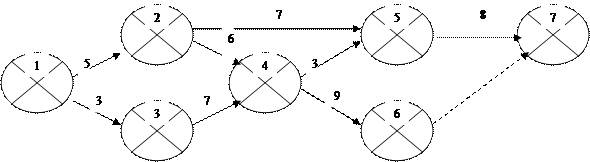Фиктивная работа (6,7) введена для того, чтобы было одно завершающее событие.

1 этап. При вычислении t_p(i) перемещаемся по сетевому графику от исходного события 1 к завершающему событию 7.

t_p (1) = 0

В событие 2 входит только одна работа

t_p (2) = t_p (1) + t (1, 2) =0+5=5

Аналогично

t_p (3) = t_p (1) + t (1, 3) = 0+3=3

В событие 4 и 5 входят 2 работы

t_p (4) = max { t_p (2) + t (2, 4); t_p (3) + t (3, 4)} = max {5+6, 3+7} = max {11, 10} = 11

t_p (5) = max { t_p (2) + t (2, 5); t_p (4) + t (4, 5)} = max {5+7, 11+3} = max {12, 14} = 14

t_p (6) = t_p (4) + t (4, 6) = 11+9=20

t_p (7) = max { t_p (5) + t (5, 7); t_p (6) + t (6, 7)} = max {14+8; 20+0}= max {22, 20}=22

t критическое = 22

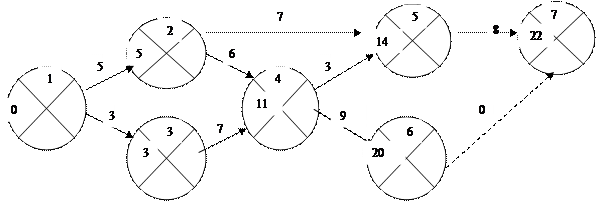2 этап. При вычислении t_n(i) перемещаемся от завершающего события 7 к исходному 1 по сетевому графику против стрелок.

t_n (7) = t_p (7) = 22

Далее рассматриваем непосредственно предшествующее событие 6, из которого выходит только одна работа (6,7)

t_n (6) = t_n (7) - t (6, 7) = 22-0 = 22

Аналогично

t_n (5) = t_n (7) - t (5, 7) = 22 - 8 = 14

Из события 4 выходят две работы: (4,5) и (4,6). Поэтому определяем t_n (4) по каждой из этих работ

t_п (4) = min { t_n (5) - t (4, 5); t_n (6) - t (4, 6)} = min {14-3, 22-10} = min {11, 12} = 11

t_n (3) = t_n (4) - t (3, 4) = 11 - 7 = 4

t_п (2) = min { t_n (5) - t (2, 5); t_n (4) - t (2, 4)} = min {14-7, 11-7} = min {7, 5} = 5

t_п (1) = min { t_n (2) - t (1, 2); t_n (3) - t (1, 3)} = min {5-5, 4-3} = min {0, 1} = 0

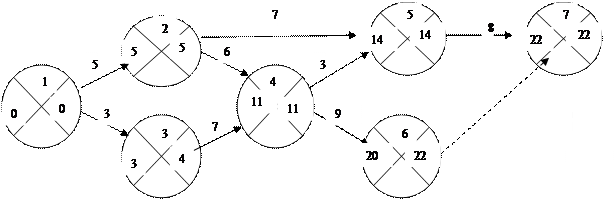3 этап.

Вычисляем R(i) = t_n(i) – t_p(i) – резерв времени события I, то есть из чисел, полученных на этапе 2, вычитаем числа, полученные на этапе 1.

4 этап.

У критических событий резерв времени равен нулю, так как ранние и поздние сроки их свершения совпадают. Критические события 1, 2, 4, 5, 7, 8 и определяют критический путь 1-2-4-5-7-8, который на сетевом графике выделен жирными линиями.

Теперь можно ответить на вопросы задачи.

Для завершения работы потребуется 22 недели. Работа (2,4) расположена на критическом пути. Поэтому её нельзя отложить без отсрочки завершения работы в целом. Работа (2,5) не расположена на критическом пути, её можно задержать на

t_n (5) – t_p (2) – t (2,5) = 14 – 5 – 7 = 2 (недели)