Пример
Необходимо определить степень согласованности мнения пяти экспертов, результаты ранжирования которыми семи объектов приведены в таблице.
| Номер объекта экспертизы | Оценка эксперта | Сумма рангов | Отклонение от среднего | Квадрат отклонения | ||||
| страна | ||||||||
| дизайн | -5 | |||||||
| цена | ||||||||
| эксклюзив | ||||||||
| состав | -13 | |||||||
| бренд | ||||||||
| универсальность | ||||||||
| 140/20 |
Оцениваем среднеарифметическое число рангов:
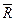 = (21 + 15 + 9 + 28 + 7 + 25 + 35)/7 = 20.
= (21 + 15 + 9 + 28 + 7 + 25 + 35)/7 = 20.
Затем оцениваем сумму квадратов отклонений от среднего: S = 630. Определяем величину коэффициента конкордации:
W = 12 * 630 / 25 * (343 - 7) = 0,9
Полученный результат свидетельствует о достаточно высокой степени согласованности экспертов.
В том случае, если W <0,33 можно провести следующие действия:
ü проанализировать состав экспертов и посмотреть мнения каких и почему выделяются из общей совокупности;
ü посмотреть среднюю оценку и из рассмотренной совокупности оценок экспертов исключить мнения аномальных;
ü процедура повторяется до тех пор пока W не будет ³ 0,33
Тесноту связи между двумя переменными можно рассчитать по коэффициенту ранговой корреляции (коэффициент корреляции рангов, коэффициент Спирмена)
Коэффициент ранговой корреляции Спирмена - это непараметрический метод, который используется с целью статистического изучения связи между явлениями. В этом случае определяется фактическая степень параллелизма между двумя количественными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента.
Практический расчет коэффициента ранговой корреляции Спирмена включает следующие этапы:
1) Сопоставить каждому из признаков их порядковый номер (ранг) по возрастанию (или убыванию).
2) Определить разности рангов каждой пары сопоставляемых значений.
3) Возвести в квадрат каждую разность и суммировать полученные результаты.
4) Вычислить коэффициент корреляции рангов по формуле:
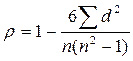
где 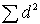 - сумма квадратов разностей рангов, а
- сумма квадратов разностей рангов, а 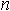 - число парных наблюдений.
- число парных наблюдений.
При использовании коэффициента ранговой корреляции условно оценивают тесноту связи между признаками, считая значения коэффициента равные 0,3 и менее, показателями слабой тесноты связи; значения более 0,4, но менее 0,7 - показателями умеренной тесноты связи, а значения 0,7 и более - показателями высокой тесноты связи.
Мощность коэффициента ранговой корреляции Спирмена несколько уступает мощности коэффициента корреляции. Разница между ними: первый рассчитывается на основе рангов, а второй – конкретные данные.
Коэффициент ранговой корреляции целесообразно применять при наличии небольшого количества наблюдений.
Пример.
Определить связь между объемом выпуска продукции и прибылью.
| № п\п | Объем выпуска продукции, тыс. ед. | Прибыль, тыс. руб. | Ранги | d=R1-R2 | d2 | |
| R1 | R2 | |||||
| 4.3 | 22.4 | -4 | ||||
| 5.4 | 18.6 | |||||
| 3.6 | 13.1 | -1 | ||||
| 6.9 | 25.1 | |||||
| 3.9 | 10.2 | |||||
| 4.7 | 19.2 | -1 | ||||
| 4.0 | 15.7 | |||||
| 6.4 | 23.4 | -1 | ||||
| 5.5 | 16.0 | |||||
| 6.8 | 21.5 |
Проранжировали показатели от минимума к максимуму. Подставляем в формулу: ρ = 1- 6*34/10(102-1)= 0,8 Вывод: связь сильная.
Литература.
- Бездудный Ф.Ф., Павлов А.П. Математические методы и модели в планировании текстильной и легкой промышленности. М., Легкая индустрия, 1979г.
- Экономико-математические методы и прикладные модели. Под ред. В.В. Федосеева. М., ЮНИТИ,2002г.
- Просветов Г.И. Математические методы в экономике. Учебно-методическое пособие. М., изд-во РДЛ, 2004г.
- Горчаков А.А., Орлова И.В. Компьютерные экономико-математические модели. М., ЮНИТИ, 1995г.
- Ветрова Г.С., Корчуганова Т.М. Экономико-математические методы и модели. Учебное пособие. РосЗИТЛП, 2005
- Лиходиевская Л.И., Экономико-математические методы и модели, Учебно-методический комплекс, РосЗИТЛП, 2009
- Просветов Г.И., Математические методы в экономике, Учебно-методическое пособие, Издательство РДЛ, 2004
- Казаков О.Л. и др, Экономико-математическое моделирование, Учебно-методическое пособие, МГИУ, 2006
- Гореева Н.М. и др., Эконометрика в схемах и таблицах, М.:Эксмо, 2008
15. Макарова С.И., Севастьянова С.А., Экономико-математические методы и модели., Задачник. М.: КНОРУС, 2009
 2014-02-02
2014-02-02 2393
2393