Сетевой моделью (другие названия: сетевой график, сеть) называется экономико-математическая модель, отражающая графическое представление технологической последовательности ведения работ.
Первые системы, использующие сетевые графики, были созданы в США в конце 50-х годов прошлого столетия для управления строительными работами. В СССР первое применение в начале 60-х годов.
Анализ сетевой модели, представленной в графической или табличной (матричной) форме, позволяет, во-первых, более четко выявить взаимосвязи этапов реализации проекта и, во-вторых, определить наиболее оптимальный порядок выполнения этих этапов в целях, например, сокращения сроков выполнения всего комплекса работ. Таким образом, методы сетевого моделирования относятся к методам принятия оптимальных решений.
В экономических исследованиях сетевые модели возникают при моделировании экономических процессов методами сетевого планирования и управления (СПУ).
Объектом управления в системах сетевого планирования и управления являются коллективы исполнителей, располагающих определенными ресурсами и выполняющих определенный комплекс операций, который призван обеспечить достижение намеченной цели, например, разработку нового изделия, строительства объекта и т.п.
Цель – спланировать и контролировать ход работ.
Основой СПУ является сетевая модель (СМ), в которой моделируется совокупность взаимосвязанных работ и событий, отображающих процесс достижения определенной цели. Она может быть представлена в виде графика или таблицы.
Основные понятия СМ: событие, работа и путь.
На рисунке графически представлена СМ, состоящая из 11 событий и 16 работ, продолжительность выполнения которых указана над работами.
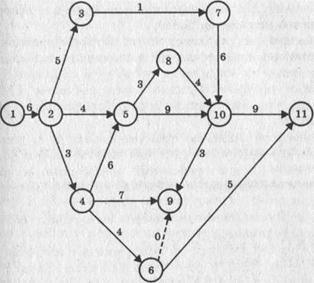 Работа – это любые действия, трудовые процессы, сопровождающиеся затратами ресурсов или времени и приводящие к определенным результатам. При графическом представлении работа изображается стрелкой, которая соединяет два события. Она обозначается парой заключенных в скобки чисел (i,j), где i — номер события, из которого работа выходит, a j — номер события, в которое она входит.
Работа – это любые действия, трудовые процессы, сопровождающиеся затратами ресурсов или времени и приводящие к определенным результатам. При графическом представлении работа изображается стрелкой, которая соединяет два события. Она обозначается парой заключенных в скобки чисел (i,j), где i — номер события, из которого работа выходит, a j — номер события, в которое она входит.
Работа не может начаться раньше, чем свершится событие, из которого она выходит. Каждая работа имеет определенную продолжительность t (ij). Например, запись t (2,5) = 4 означает, что работа (2,5) имеет продолжительность 4 единицы. Для указания того, что одна работа не может быть выполнена раньше другой, вводят понятие – фиктивные работы, к оторые изображаются пунктирными стрелками. Продолжительность фиктивной работы принимается равной нулю. (см. работу (6,9)).
Событие - результаты выполнения одной или нескольких работ, условие начала выполнения какой-либо работы. Не имеет протяженности во времени. Событие свершается в тот момент, когда оканчивается последняя из работ, входящая в него. События обозначаются одним числом и при графическом представлении СМ изображаются кружком (или иной геометрической фигурой), внутри которого проставляется его порядковый Номер (i = 1, 2,..., N). Ни одна, выходящая из данного события работа не может начаться до окончания всех работ, входящих в это событие.В СМ имеется начальное событие (с номером 1), из которого работы только выходят, и конечное событие (с номером N), в которое работы только входят.
Путь — это цепочка следующих друг за другом работ, соединяющих начальную и конечную вершины, например, в
 приведенной выше модели путями являются L1= (1, 2, 3, 7, 10, 11), L 2 = (1, 2, 4, 6, 11) и др.
приведенной выше модели путями являются L1= (1, 2, 3, 7, 10, 11), L 2 = (1, 2, 4, 6, 11) и др.
Продолжительность пути определяется суммой продолжительностей составляющих его работ. Путь, имеющий максимальную длину, называют критическим и обозначают Lкр, а его продолжительность — tкр. Работы, принадлежащие критическому пути, называются критическими. Их несвоевременное выполнение ведет к срыву сроков всего комплекса работ.
СМ имеют ряд характеристик, которые позволяют определить степень напряженности выполнения отдельных работ, а также всего их комплекса и принять решение о перераспределении ресурсов.
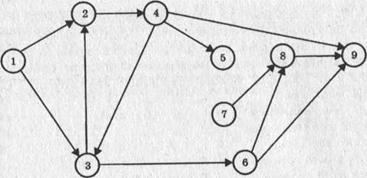 |
Перед расчетом СМ следует убедиться, что она удовлетворяет следующим основным требованиям:
1.События правильно пронумерованы, т. е. для каждой работы (i, j) i < j (см. на рис. работы (4,3) и (3,2)). При невыполнении этого требования необходимо использовать алгоритм перенумерации событий, который заключается в следующем:
ü нумерация событий начинается с исходного события, которому присваивается № 1;
ü из исходного события вычеркивают все исходящие из него работы (стрелки), и на оставшейся сети находят событие, в которое не входит ни одна работа, ему и присваивают № 2;
ü затем вычеркивают работы, выходящие из события № 2, и вновь находят событие, в которое не входит ни одна работа, и ему присваивают № 3, и так продолжается до завершающего события, номер которого должен быть равен количеству событий в сетевом графике;
ü если при очередном вычеркивании работ одновременно несколько событий не имеют входящих в них работ, то их нумеруют очередными номерами в произвольном порядке.
2. Исходное событие лишь одно.
3. Завершающее событие – одно.
4. Отсутствуют тупиковые события (кроме завершающего), т. е. такие, за которыми не следует хотя бы одна работа (событие 5);
5. Отсутствуют события (за исключением исходного), которым не предшествует хотя бы одна работа (событие 7);
6. Отсутствуют циклы, т. е. замкнутые пути, соединяющие событие с ним же самим (см. путь (2,4,3)).
При невыполнении указанных требований бессмысленно приступать к вычислениям характеристик событий, работ и критического пути.
 2014-02-02
2014-02-02 1462
1462
