2014-02-04
991
Дифференцируемость функций нескольких переменных.
Напомним, что функция одной переменной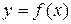 
называется дифференцируемой в точке 
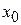, если приращение функции представимо в виде
,
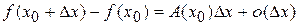где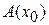 
― некоторое действительное число, зависящее от 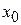, а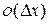 
- бесконечно малая функция более высокого порядка малости, чем 
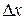, при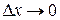 
.
Необходимым и достаточным условием дифференцируемости функции 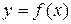в точке 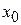является существование производной
