Дифференцирование функций нескольких переменных
Пусть 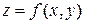 — функция двух независимых переменных и D
— функция двух независимых переменных и D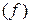 — область ее определения. Выберем произвольную точку
— область ее определения. Выберем произвольную точку 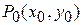 ÎD
ÎD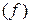 и дадим
и дадим 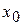 приращение
приращение 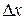 , а значение
, а значение  оставим неизменным. При этом функция
оставим неизменным. При этом функция 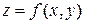 получит приращение
получит приращение
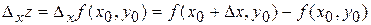 ,
,
которое называется частным приращением функции 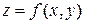 по переменной
по переменной 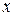 в точке
в точке 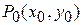 .
.
Аналогично, считая 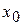 постоянной и придавая
постоянной и придавая  приращение
приращение 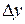 , получаем частное приращение функции
, получаем частное приращение функции 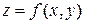 по переменной
по переменной 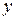 в точке
в точке 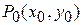 :
:
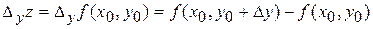 .
.
Полным приращением функции 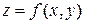 в точке
в точке 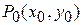 называют разность
называют разность
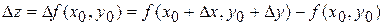 .
.
Замечание. В общем случае полное приращение не равно сумме частных приращений, т.е.  .
.
Геометрически частные и полное приращения функции 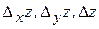 можно изобразить отрезками
можно изобразить отрезками 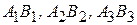 .
.
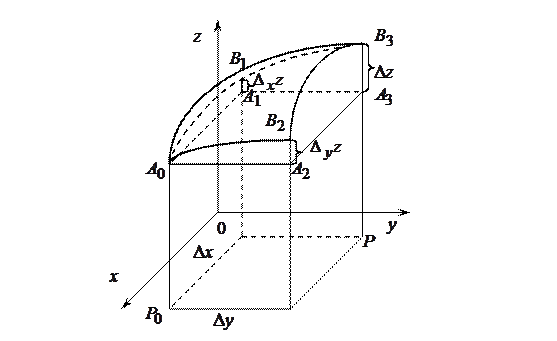
Пример. Найти частные и полное приращения функции  в точке
в точке 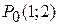 , если
, если 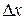 = 0,2,
= 0,2, 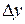 = 0,3.
= 0,3.
Решение. По определению найдем частные приращения:
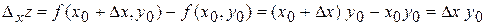 ,
,
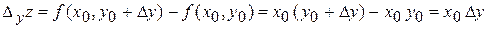 .
.
Найдем полное приращение функции:
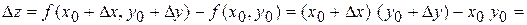
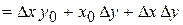 .
.
При 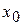 =1,
=1,  =2,
=2, 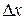 =0,2,
=0,2, 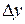 =0,3:
=0,3:  = 0,2×2 = 0,4,
= 0,2×2 = 0,4,
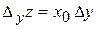 =1×0,3 = 0,3,
=1×0,3 = 0,3,
 0,4 + 0,3 +0,2×0,3 = 0,76,
0,4 + 0,3 +0,2×0,3 = 0,76,
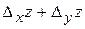 =0,4 + 0,3 = 0,7,
=0,4 + 0,3 = 0,7,
0,7¹0,76,
т.е. мы получили, что при таких условиях  .
.
Аналогично определяют частные и полное приращения функции n переменных 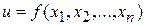 .
.
 2014-02-04
2014-02-04 5740
5740
