.
.
.
Замечание. Если вычислить интеграл, считая область стандартной относительно оси 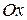 , мы получим тот же результат:
, мы получим тот же результат:
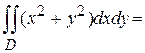
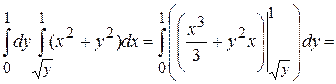
Пример. Вычислить двойной интеграл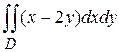 по области
по области  , ограниченной линиями:
, ограниченной линиями: 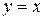 ,
, 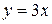 ,
, 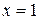 .
.
Решение. Изобразим на рисунке заданную область интегрирования.
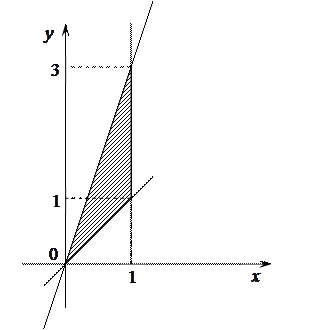
Данная область является стандартной относительно оси 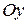 .
.
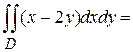
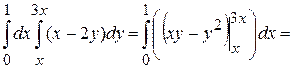

Пример. Изменить порядок интегрирования в повторном интеграле:
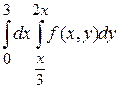
Решение. Изобразим на рисунке область интегрирования.
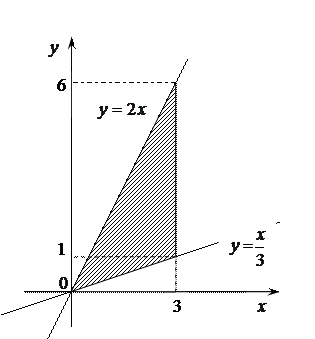
Из пределов интегрирования находим линии, ограничивающие область интегрирования: 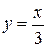 ,
, 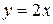 ,
, 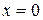 ,
, 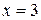 . Для изменения порядка интегрирования выразим
. Для изменения порядка интегрирования выразим 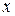 как функции от
как функции от 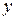 и найдем точки пересечения:
и найдем точки пересечения:
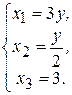
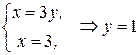 ,
, 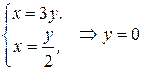 ,
, 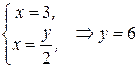 .
.
Так как на одном из интервалов функция 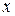 выражена двумя аналитическими выражениями, то область интегрирования необходимо разбить на две области, а повторный интеграл представить как сумму двух интегралов.
выражена двумя аналитическими выражениями, то область интегрирования необходимо разбить на две области, а повторный интеграл представить как сумму двух интегралов.
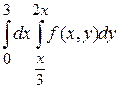
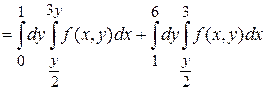 .
.
 2014-02-04
2014-02-04 808
808








