Свойства двойного интеграла

Двойной интеграл обладает свойствами, аналогичными свойствам определенного интеграла. Отметим лишь основные из них:

1. Если функции и и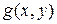нтегрируемы в области , то интегрируемы в ней их сумма и разность, причем

.

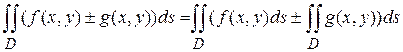2. Постоянный множитель можно выносить за знак двойного интеграла:

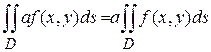
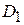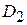3. Если интегрируема в области , а эта область разбита на две непересекающиеся области и , то

.

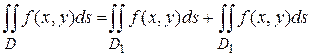4. Если и и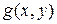нтегрируемы в области , в которой 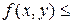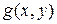, то

.

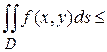
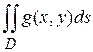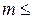
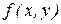
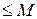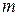5. Если в области функция удовлетворяет неравенствам ,где и 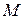¾ некоторые действительные числа, то

,

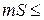
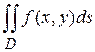
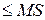где 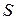– площадь области .

Доказательства этих свойств аналогичны доказательству соответствующих теорем для определенного интеграла.