Задачи, приводящие к двойным интегралам.
Кратные интегралы
Задача об объеме цилиндроида. Рассмотрим тело с основанием  , лежащим в плоскости
, лежащим в плоскости 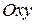 , ограниченное поверхностью
, ограниченное поверхностью 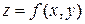 и цилиндрической поверхностью, образующие которой параллельны оси
и цилиндрической поверхностью, образующие которой параллельны оси 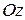 , а направляющей служит граница области
, а направляющей служит граница области  . Это тело называется цилиндроидом (цилиндрическим брусом, или общим цилиндром). Требуется вычислить объем цилиндроида.
. Это тело называется цилиндроидом (цилиндрическим брусом, или общим цилиндром). Требуется вычислить объем цилиндроида.
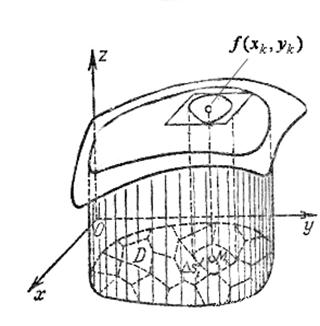
Чтобы решить задачу, область  разобьем произвольным образом на
разобьем произвольным образом на 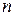 частей
частей 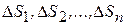 , площади которых также обозначим через
, площади которых также обозначим через 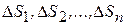 соответственно. В каждой из элементарных областей
соответственно. В каждой из элементарных областей 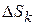 (
(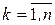 ) выберем произвольную точку
) выберем произвольную точку 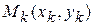 и значение функции в этой точке
и значение функции в этой точке 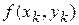 умножим на площадь области
умножим на площадь области 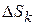 . Это произведение
. Это произведение 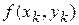
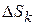 равно объему цилиндрического тела с площадью основания
равно объему цилиндрического тела с площадью основания 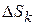 и высотой
и высотой 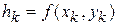 . Составим сумму всех таких произведений:
. Составим сумму всех таких произведений:
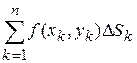 .
.
Эта сумма выражает объем 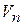 ступенчатого цилиндрического тела, приближенно заменяющего данный цилиндроид,
ступенчатого цилиндрического тела, приближенно заменяющего данный цилиндроид,
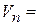
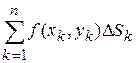 .
.
Обозначим диаметр элементарной области 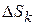 через
через 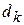 , то есть наибольшее расстояние между точками, лежащими на границе области, а наибольший из этих диаметров — через
, то есть наибольшее расстояние между точками, лежащими на границе области, а наибольший из этих диаметров — через 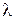 . Очевидно, если
. Очевидно, если 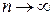 , то
, то 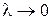 .Объемом общего цилиндра является предел объема соответствующего ступенчатого тела при
.Объемом общего цилиндра является предел объема соответствующего ступенчатого тела при 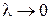 :
:

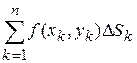 .
.
Задача о массе пластинки. Рассмотрим область  плоскости
плоскости 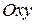 , ограниченную замкнутой линией, в которой распределено вещество с плотностью
, ограниченную замкнутой линией, в которой распределено вещество с плотностью 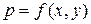 . Такую область называют пластинкой. Вычислим массу пластинки, предположив известной функцию
. Такую область называют пластинкой. Вычислим массу пластинки, предположив известной функцию 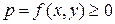 .
.
Область  произвольным образом разобьем на области
произвольным образом разобьем на области 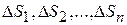 , площади которых обозначим теми же символами. Предположим, что в каждой элементарной области
, площади которых обозначим теми же символами. Предположим, что в каждой элементарной области 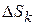 плотность постоянна и равна плотности в некоторой точке
плотность постоянна и равна плотности в некоторой точке 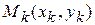 этой области, т. е.
этой области, т. е. 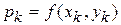 . Тогда произведение
. Тогда произведение 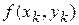
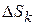 выражает приближенную массу элементарной пластинки
выражает приближенную массу элементарной пластинки 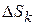 , а сумма всех таких произведений — приближенную массу
, а сумма всех таких произведений — приближенную массу 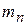 всей пластинки, т. е.
всей пластинки, т. е.
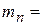
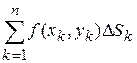 .
.
Точное значение массы всей пластинки получим, перейдя к пределу при 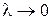 , где
, где 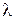 — наибольший из диаметров
— наибольший из диаметров 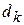 области
области 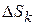 :
:
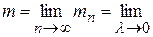
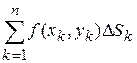 .
.
Обе задачи привели к необходимости рассмотрения двумерной интегральной суммы
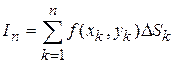
для функции  по области
по области  и ее предела при
и ее предела при 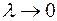 .
.
Определение. Число 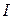 называется пределом интегральной суммы
называется пределом интегральной суммы 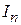 при
при 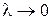 , если для любого числа
, если для любого числа 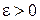 можно указать такое число
можно указать такое число 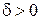 , что при
, что при 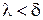 выполняется неравенство
выполняется неравенство
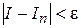
независимо от выбора точек 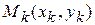 в элементарных областях
в элементарных областях 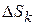 .
.
Определение. Двойным интегралом от функции  по области
по области  называется предел ее интегральной суммы при
называется предел ее интегральной суммы при 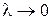 , если он существует и не зависит от способа разбиения области и выбора точек
, если он существует и не зависит от способа разбиения области и выбора точек 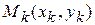 :
:
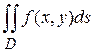
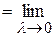
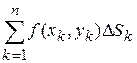 .
.
При этом функция  называется подынтегральной функцией, а область
называется подынтегральной функцией, а область  — областью интегрирования.
— областью интегрирования.
Двойной интеграл от функции  по области
по области  обозначается также следующим образом:
обозначается также следующим образом:
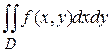 .
.
Отметим без доказательства, что предел интегральной суммы существует, если функция 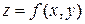 непрерывна в замкнутой области, имеющей площадь. Если предел интегральной суммы существует, то функция
непрерывна в замкнутой области, имеющей площадь. Если предел интегральной суммы существует, то функция  называется интегрируемой в области
называется интегрируемой в области  . Следовательно, все непрерывные функции являются интегрируемыми, среди разрывных функций имеются интегрируемые и неинтегрируемые.
. Следовательно, все непрерывные функции являются интегрируемыми, среди разрывных функций имеются интегрируемые и неинтегрируемые.
Из решения задач, рассмотренных выше, следует геометрический и физический смысл двойного интеграла:
1. Геометрический смысл: двойной интеграл от функции  r
r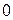 по области
по области  равен объему цилиндроида с основанием
равен объему цилиндроида с основанием  , который ограничен сверху поверхностью
, который ограничен сверху поверхностью 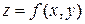
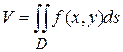 .
.
2. Физический смысл двойного интеграла: если неотрицательная функция 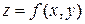 выражает поверхностную плотность пластинки
выражает поверхностную плотность пластинки  , то ее масса равна двойному интегралу от данной функции по данной области
, то ее масса равна двойному интегралу от данной функции по данной области 
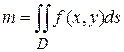 .
.
 2014-02-04
2014-02-04 3540
3540
