Формула Грина устанавливает связь между двойным интегралом по области  и криволинейным интегралом по контуру
и криволинейным интегралом по контуру 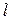 , ограничивающему эту область. Будем считать, что область
, ограничивающему эту область. Будем считать, что область  является стандартной в направлении каждой координатной оси и снизу ограничена графиком функции
является стандартной в направлении каждой координатной оси и снизу ограничена графиком функции 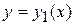 (дугой
(дугой 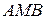 ),сверху — графиком функции
),сверху — графиком функции 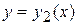 (дугой
(дугой 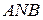 ),которые вместе составляют замкнутый контур
),которые вместе составляют замкнутый контур 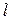 .
.
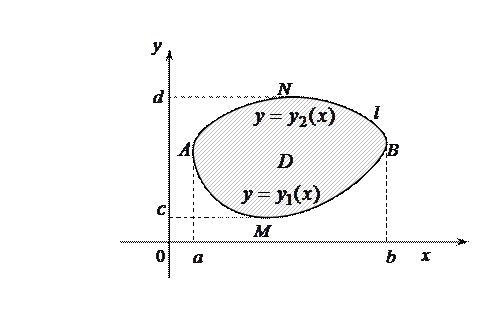
Пусть в области  и на ее границе
и на ее границе 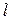 заданы функции
заданы функции 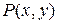 и
и 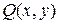 непрерывные вместе со своими частными производными
непрерывные вместе со своими частными производными 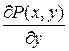 ,
, 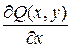 ,тогда
,тогда
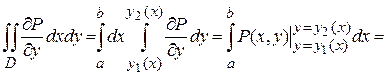
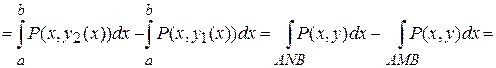
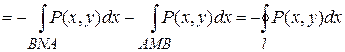 ,
,
где обход контура 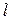 совершается в положительном направлении, т. е. против часовой стрелки (область
совершается в положительном направлении, т. е. против часовой стрелки (область  остается слева). Следовательно,
остается слева). Следовательно,
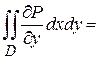
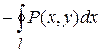 . (1)
. (1)
Аналогично получаем
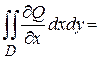
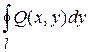 , (2)
, (2)
где обход контура 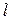 также совершается в положительном направлении.
также совершается в положительном направлении.
Вычитая почленно (1) из (2), получаем формулу Грина
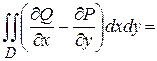
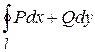 .
.
Замечание 1. Если обход контура 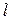 совершается в отрицательном направлении, т. е. по часовой стрелке (область
совершается в отрицательном направлении, т. е. по часовой стрелке (область  остается справа), то формула Грина принимает вид
остается справа), то формула Грина принимает вид
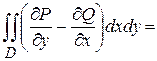
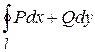 .
.
Замечание 2. Формула Грина дает возможность вычислять площадь области с помощью криволинейного интеграла. Действительно, если 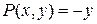 ,
, 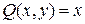 , то формула Грина перепишется так:
, то формула Грина перепишется так:
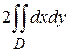
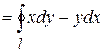 ,
,
откуда
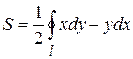 , (3)
, (3)
где обход контура 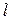 совершается против часовой стрелки.
совершается против часовой стрелки.
Пример. Определить с помощью криволинейного интеграла площадь, ограниченную эллипсом с полуосями 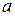 и
и 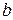 .
.
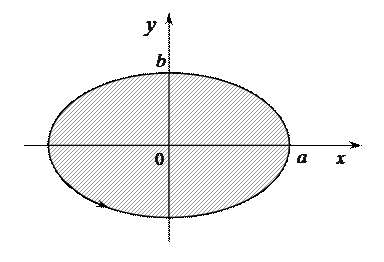
Решение. Запишем параметрические уравнения эллипса
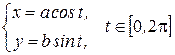 .
.
Тогда
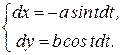
И по формуле (3) получим
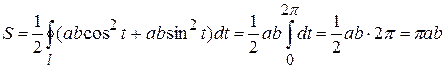 .
.
 2014-02-04
2014-02-04 1823
1823








