При определении криволинейного интеграла второго рода элементарная работа 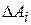 силы
силы 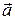 на участке
на участке 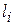 находилась как скалярное произведение вектора
находилась как скалярное произведение вектора 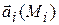 и вектора, приближенно равного по длине и направлению участку
и вектора, приближенно равного по длине и направлению участку 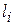 . Вместо вектора
. Вместо вектора 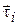
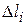 , в качестве вектора, близкого к
, в качестве вектора, близкого к 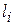 можно взять вектор
можно взять вектор 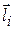 , начало и конец которого совпадают с началом и концом участка
, начало и конец которого совпадают с началом и концом участка 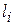 .
.
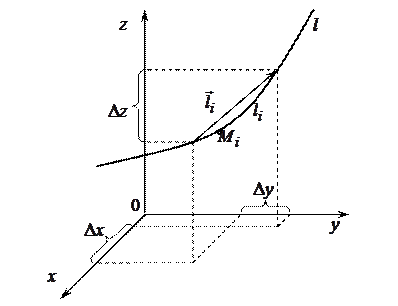
Найдем скалярное произведение векторов 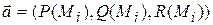 и
и 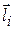
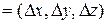 в координатной форме как сумму произведений соответствующих координат:
в координатной форме как сумму произведений соответствующих координат:
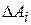
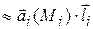
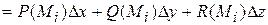
Переходя к пределу при 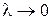 , где
, где 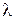 ― длина наибольшей из элементарных дуг
― длина наибольшей из элементарных дуг 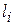 , получаем точное значение работы
, получаем точное значение работы
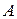
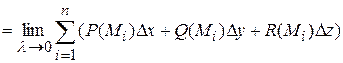 .
.
Следовательно, криволинейный интеграл второго рода в скалярной координатной форме имеет вид:
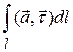
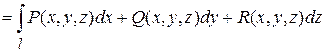
или, в более краткой форме
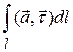
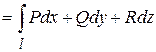 .
.
Вычисление криволинейных интегралов второго рода
Пусть линия 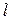 задана параметрически
задана параметрически
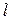 :
: 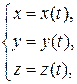
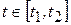 .
.
Тогда по определению дифференциала
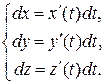
Отметим начало дуги 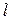 точкой
точкой 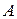 , конец — точкой
, конец — точкой 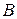 . В этом случае говорят, что задано направление перемещения по кривой от точки
. В этом случае говорят, что задано направление перемещения по кривой от точки 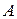
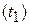 к точке
к точке 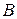
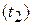 и тем самым указано направление ориентирующего вектора
и тем самым указано направление ориентирующего вектора 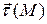 .
.
Покажем, что вычисление криволинейного интеграла второго рода по линии 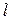 заданной параметрически, сводится к вычислению однократного определенного интеграла по параметру
заданной параметрически, сводится к вычислению однократного определенного интеграла по параметру 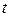 :
:
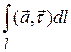
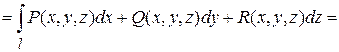
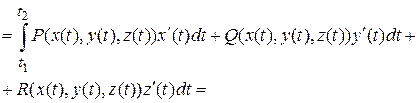
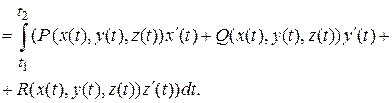
А в случае плоской кривой, когда 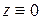 , последняя формула примет вид:
, последняя формула примет вид:
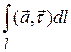
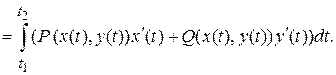
Замечание. Для плоской кривой, заданной уравнением 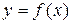 ,
, 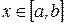 криволинейный интеграл второго рода в координатной скалярной форме сводится к определенному интегралу по переменной
криволинейный интеграл второго рода в координатной скалярной форме сводится к определенному интегралу по переменной 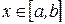
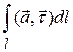
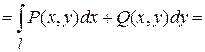
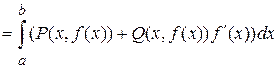
(Выбрана ориентация 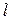 , при которой
, при которой 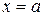 ,
, 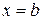 соответствуют началу и окончанию пути интегрирования.)
соответствуют началу и окончанию пути интегрирования.)
Если кривая 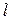 задана уравнением
задана уравнением 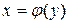 ,
, 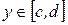 , то при соответствующей ориентации интегрирование по переменной
, то при соответствующей ориентации интегрирование по переменной 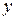 будет осуществляться от
будет осуществляться от 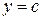 до
до 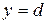 :
:
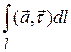
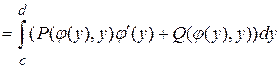 .
.
Пример. Вычислить 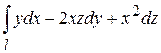 , где
, где 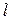 — отрезок прямой с началом в точке
— отрезок прямой с началом в точке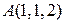 и концом в точке
и концом в точке  .
.
Решение. Изобразим на рисунке линию интегрирования.
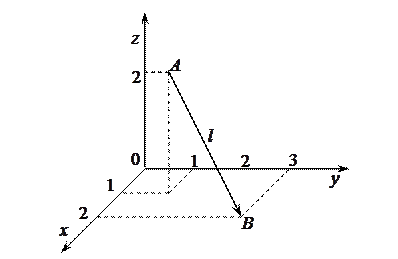
Воспользуемся формулами параметрических уравнений прямой с направляющим вектором 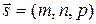 , проходящей через начальную точку с координатами
, проходящей через начальную точку с координатами 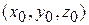 :
:
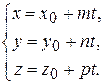
Запишем параметрические уравнения прямой, которой принадлежит отрезок 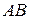 , приняв за направляющий вектор прямой
, приняв за направляющий вектор прямой 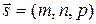 вектор
вектор 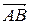 .
.
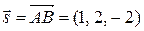 .
.
Начальной точкой отрезка 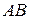 является точка
является точка 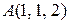 . Следовательно, параметрические уравнения этой прямой:
. Следовательно, параметрические уравнения этой прямой:
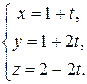
Из полученных уравнений находим, что точке 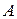 соответствует значение параметра
соответствует значение параметра 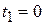 , а точке
, а точке 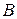 значение
значение 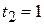 .
.
По определению дифференциала
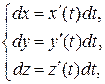
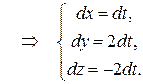
Подставляя в интеграл значения 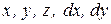 и
и 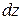 , а также учитывая значения параметра
, а также учитывая значения параметра  и
и 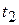 , соответствующие началу и концу дуги
, соответствующие началу и концу дуги 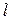 , получим:
, получим:
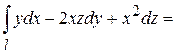
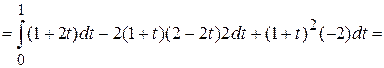
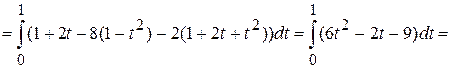
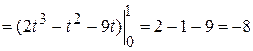 .
.
Пример. Вычислить 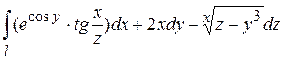 , где
, где 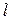 — отрезок прямой с началом в точке
— отрезок прямой с началом в точке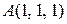 и концом в точке
и концом в точке 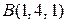 .
.
Решение. Изобразим на рисунке линию интегрирования.
|
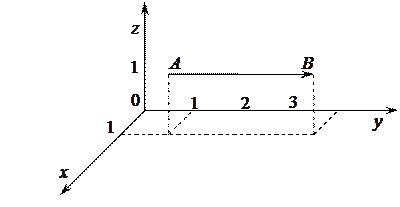
Воспользуемся формулами параметрических уравнений прямой с направляющим вектором 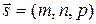 , проходящей через начальную точку с координатами
, проходящей через начальную точку с координатами 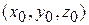 :
:
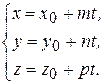
Запишем параметрические уравнения прямой, которой принадлежит отрезок 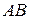 , приняв за направляющий вектор прямой
, приняв за направляющий вектор прямой 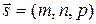 вектор
вектор 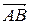 , т. е.
, т. е. 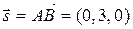 .
.
Начальной точкой отрезка 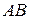 является точка
является точка 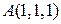 . Следовательно, параметрические уравнения этой прямой:
. Следовательно, параметрические уравнения этой прямой:
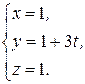
Из полученных уравнений находим, что точке 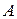 соответствует значение параметра
соответствует значение параметра 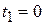 , а точке
, а точке 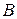 значение
значение 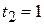 .
.
По определению дифференциала
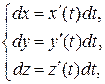
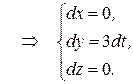
Учитывая, что 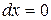 и
и 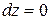 , подставляем в интеграл только значения
, подставляем в интеграл только значения 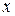 и
и 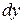 , а также значения параметра
, а также значения параметра  и
и 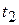 , соответствующие началу и концу дуги
, соответствующие началу и концу дуги 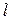
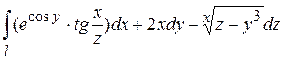
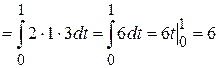 .
.
Пример. Вычислить 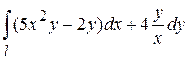 , где
, где 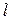 —плоская кривая, являющаяся частью параболы
—плоская кривая, являющаяся частью параболы 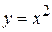 от точки
от точки 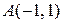 до точки
до точки 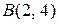 .
.
Решение. Изобразим на рисунке линию интегрирования 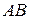 .
.
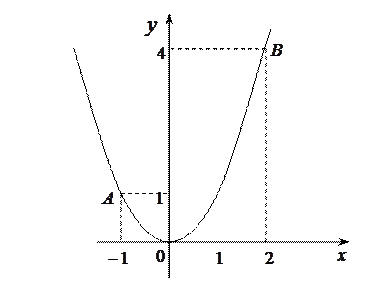
Воспользуемся формулой:
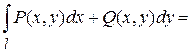
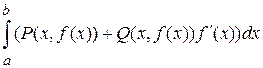
В данном случае 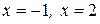 соответствуют началу и окончанию пути интегрирования,
соответствуют началу и окончанию пути интегрирования, 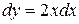 , следовательно:
, следовательно:
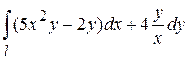
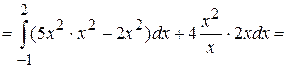
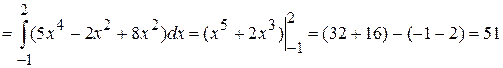 .
.
 2014-02-04
2014-02-04 1268
1268