1. Пусть А={1, 2, 3, 4, 10, 20}, В={6, 10, 11, 15}. Найти А 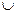 В.
В.
2. Пусть С={100, 105, 106 120}, D={95, 100, 105, 130, 140}. Найти А  D.
D.
3. Пусть А={a, b, d, e, f, i, j}, В={e, f, i, k, l, m}. Найти А\В, B\A.
4. Пусть U={1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, F={2, 3, 5, 6, 7}. Найти 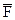 .
.
Свойства операций объединения и пересечения
Для произвольных множеств А, В, С выполняются следующие соотношения.
1. Идемпотентность (А А=А; A
А=А; A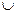 A=A).
A=A).
2. Коммуникативность (А В=В
В=В А; A
А; A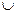 В=В
В=В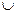 A).
A).
3. Ассоциативность ((А В)
В)  С=А
С=А (В
(В С); (А
С); (А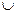 В)
В) 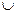 С=А
С=А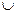 (В
(В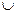 С)).
С)).
4. Дистрибутивность (А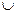 (В
(В  С) = (А
С) = (А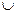 В)
В)  (А
(А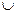 С);
С);
А (В
(В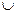 С) = (А
С) = (А В)
В) 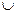 (А
(А С)).
С)).
5. Поглощение ((А В)
В) 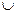 A=А; (А
A=А; (А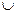 В)
В)  A=А).
A=А).
6. Свойство нуля (А Ø=Ø; А
Ø=Ø; А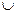 Ø=А).
Ø=А).
7. Свойство единицы (А U=A; A
U=A; A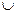 U=U).
U=U).
8. Инволютивность (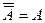 ).
).
9. 
 Законы де Моргана (
Законы де Моргана (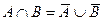 ,
,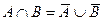 ).
).
10. Свойства дополнения (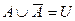 ,
,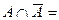 Ø).
Ø).
. Диаграммы Венна
Диаграммы Венна - геометрические представления множеств. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его замкнутых фигур), представляющих множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств.
Приведенные на рис. 1.2 - 1.5 иллюстрации операций объединения, пересечения, разности и дополнения двух множеств являются диаграммами Венна.
Пример 1. Представить множество А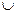 (В
(В 
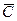 ) диаграммой Венна.
) диаграммой Венна.
Начнем с общей диаграммы, показанной на рис. 1.6,а.
Заштрихуем В диагональными линиями в одном направлении, а 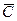 - в другом (рис. 1.6, б). Площадь с двойной штриховкой представляет собой их пересечение, т.е. множество (В
- в другом (рис. 1.6, б). Площадь с двойной штриховкой представляет собой их пересечение, т.е. множество (В 
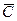 ). Выделим это множество жирной линией. На новой копии диаграммы заштрихуем эту область (В
). Выделим это множество жирной линией. На новой копии диаграммы заштрихуем эту область (В 
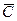 ) линиями одного направления, a A - другого. Вся заштрихованная на рис. 1..6,в область представляет объединение множеств А
) линиями одного направления, a A - другого. Вся заштрихованная на рис. 1..6,в область представляет объединение множеств А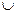 (В
(В
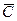 ), т.е. множество А
), т.е. множество А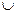 (В
(В 
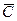 ). Обведем искомую область также жирной линией.
). Обведем искомую область также жирной линией.
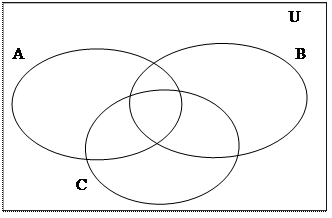
Рисунок 1.6, а



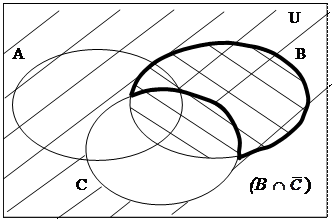
Рисунок 1.6, б
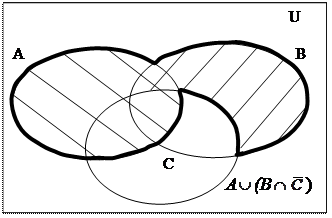
Рисунок 1.6, в
 2014-02-04
2014-02-04 914
914








