Отношения

Упражнения.

Пусть А, В, С 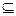U. Проиллюстрировать на примере конкретных множеств и с помощью диаграмм Венна справедливость следующих соотношений:

1. ,

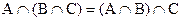2. ,

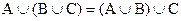3. ,

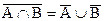4. ,

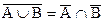5. ,

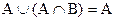6. ,

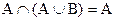7. ,

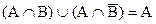8. ,

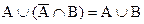Отношения - один из способов задания взаимосвязей между элементами множества. Наиболее изученными и чаще всего используемыми являются так называемые унарные и бинарные отношения.

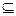Унарные (одноместные) отношения отражают наличие какого-то определенного признака R (свойства и т.п.) у эле­ментов множества М (например, "быть белым" на множестве шаров в урне). Тогда все такие элементы а из множе­ства М, которые отличаются данным признаком R, образуют некоторое подмножество в М, называемое унарным отношением R, т.е. а R и RМ.

Бинарные (двухместные) отношения используются для определения каких-то взаимосвязей, которыми характеризуются пары элементов в множестве М (так, на множестве людей могут быть заданы, например, следующие бинарные отношения: "жить в одном городе", "быть моложе", "быть сыном", "работать в одной организации" и т.п.). Тогда все пары (а, b) элементов из М, между которыми имеет место данное отношение R, образуют подмножество пар из множества всех возможных пар элементов М×М=М², называемое бинарным отношением R, т.е. (a, b)R, при этом R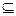М×М.

В общем случае могут рассматриваться п-местные от­ношения, например отношения между тройками элементов -трехместные (тернарные) отношения и т.д.