Пути в сетях

6 7 8 9 10 11 12

Способы задания графов

Упражнения

1. Задать графы G₂ - G₃ (см. рисунок 2.3) множествами их вершин и ребер. Сравнить графы G₁ - G₃ (см. пример 1).

2. Равны ли графы G₁ - G₂ на рисунке 2.5? Задать графы G₁ - G₃ множествами их вершин и ребер. Сравнить графы.

3. Определить дополнение графа G, если:

a) G - пятиугольник;

б) G - треугольник.

Выше мы познакомились с двумя способами описания графов: графическим, и в виде двух множеств вершин V и ребер Е, когда каждое ребро е 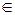Е определено парой инцидентных ему концевых вершин (v', v "). Рассмотрим другие способы, используемые в теории графов.

В общем, виде задать граф - значит, описать множества его вершин и ребер, а также отношение инцидентности. Для описания вершин и ребер достаточно их занумеровать. Пусть v₁, v₂,..., v_j...,v_n - вершины графа G: е₁, е₂,..., е_j,..., е_т – ребра. Отношение инцидентности задается:

1) матрицей инцидентности ||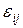 ||размера т хn: по вертикали и горизонтали указываются вершины и ребра соответственно, а на пересечении i-й вершины и j-го ребра в случае неориентированного графа проставляется 1, если они инцидентны, и 0 — в противном случае, т.е.

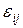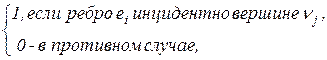
а в случае орграфа: -1, если вершина является началом ребра, 1 - если вершина является концом ребра, и 0 - если вершина и ребро не инцидентны; если некоторая вершина является для ребра и началом, и концом (т.е. ребро - петля), проставляется любое другое число, например 2, т.е.

2) скам ребер графа, представленным двумя столбцами: в левом перечисляются все ребра е_i 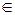Е, а в правом -инцидентные ему вершиныдля н-графа порядок вершин в строке произволен, для орграфа первым стоит номер начала ребра;

3) атрицей смежности ||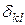|| - квадратной матрицей размера п х п: по вертикали и горизонтали перечисляются все вершины 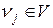, а на пересечении k-й и l -й вершин в случае н-графа проставляется число, равное числу ребер, соединяющих эти вершины; для орграфа 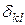равно числу ребер с началом в k- йвершине и концом в l- й.

Если два графа равны, то их матрицы совпадают. Если в графе поменять нумерацию вершин, матрицы (и список ребер) в общем случае изменяются, т.е. вид матриц и списка ребер зависит от нумерации вершин и ребер графа. Строго говоря, граф считается полностью заданным, если нумерация его вершин зафиксирована. Графы, отличающиеся только нумерацией вершин, являются изоморфными. Проверка изоморфности графов - в общем случае трудоемкая задача.

Пример 1. Задать матрицами инцидентности и смежности, а также списком ребер графы G₁, G₃ (см. рисунок 2.6).

Матрицы инцидентности графов G₁ и G₃ приведены на рисунке 2.7. В матрице инцидентности в каждом столбце только два элемента, отличных от 0 (или один, если ребро - петля).

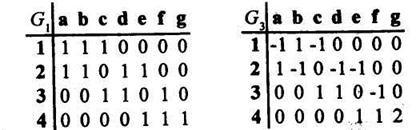
Рисунок 2.7

Список ребер является более компактным описанием графа. Список ребер орграфа G₃ приведен на рисунке 2.8, для н-графа G₁ он аналогичен, однако последовательность указания вершин здесь безразлична.

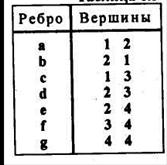
Рисунок 2.8

Матрицы смежности графов даны на рисунке 2.9.

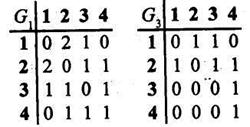
Рисунок 2.9

2.4. Сети и их свойства[1]

(Кудрявцева А. Группа ПС-285)

Иногда возникает необходимость рассматривать графы, ребрам которых поставлено в соответствие некоторое число.

Ориентированный граф N = (V,D,a) где V – множество вершин графа, D – множество дуг графа, а a - функция из множества вершин графа в множество неотрицательных действительных чисел называется сетью.

Если е – дуга графа, то число a(е) в зависимости от контекста называется либо длиной, либо весом, либо пропускной способностью дуги. При изображении сети a(е) проставляется рядом с дугой е.

Для сетей можно обобщить понятие полустепени исхода и полустепени захода вершины. Пусть N = (V,D,a) – сеть, v – вершина этой сети. Полустепенью исхода 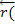v) вершины v называется сумма a(е) по всем дугам, исходящим из v, полустепенью захода 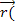v) вершины v – сумма a(е) по всем дугам, заходящим в v. Для сетей, так же как и для орграфов справедливо утверждение о том, что сумма полустепеней исхода и сумма полустепеней захода всех вершин совпадают.

Как и в случае орграфов, вершина сети v, для которой 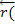v)>0 и 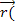v)=0 называется источником, а вершина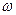, для которо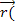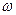й )>0 и 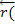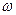)=0 – стоком.

Путь – этопоследовательность дуг, такая, что конец одной дуги является началом другой дуги.

Длиной пути называется сумма длин дуг, составляющих путь.

Длина кратчайшего (u,v)–путиназывается расстоянием d(u,v) от вершины u до вершины v. Если (u,v)–пути не существует, то d(u,v)=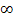. Расстояние от u до u равно нулю.

Для сети N возникает задача нахождения расстояния d(u,v) для данных вершин u и v и соответствующего кратчайшего пути.

Задача о кратчайшем пути (ЗКП) между фиксированными вершинами формулируется следующим образом: в заданной сети N с двумя выделенными вершинами v₀ и v найти кратчайший (v₀,v)-путь.

Алгоритм Форда-Беллмана ⁽²⁾

Данный алгоритм был предложен независимо Ричардом Беллманом (1958) и Лестером Фордом (1956).

Будем считать, что количество вершин n сети 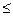количества ребер m сети и в сети нет контуров отрицательной длины.

Первый этап – вычисление расстояний от v₀ до всех остальных вершин.

Основная идея алгоритма Форда-Беллмана заключается в поэтапном вычислении кратчайших расстояний. Обозначим через d_k(v) длину кратчайшего среди всех (v₀,v) путей, содержащих не более чем k дуг. Тогда будут справедливы следующие неравенства:

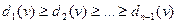Т.к. по предположению в графе нет контуров отрицательной длины, кратчайший (v,v₀)-путь не может содержать более чем n-1 дуг. Поэтому величина 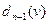дает искомое расстояние от v₀ до v.

Для вычисления d_n_-1(v) достаточно последовательно вычислять d_k(v) для всех k =1,…,n-1.

Значения d₁(v) вычисляются просто:

d₁(v) = d(v₀,v) для всех v V.

Пусть значения d_k_-1(v) вычислены для всех v V. Легко видеть, что

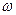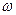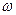
d_k_-1(v) = min{d_k(v), d_k()+d(, v)|V}.

Организовать все эти вычисления можно с помощью всего лишь одномерного массива D длины n.Положив D[ v ] = d(v₀,v) для всех вершин v V, будем иметь равенства

D[ v ] = d₁(v).

Просматривая после этого вершины v, произведем пересчет значений D[ v ] по формуле

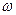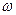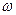
D[ v ] = min{D[ v ], D[] + d(, v)|V}.

После завершения первого пересчета значений D[ v ] для всех v, будем иметь неравенства D[ v ] 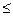d₂(v). Повторив n-2 раза процесс пересчета D[ v ], будем иметь равенства D[ v ] = d_n_-1(v), т.е. D[ v ] дает расстояние от v₀ до v.

Еще один алгоритм - алгоритм Дейкстры, названный в честь известного скандинавского специалиста по компьютерным наукам Дейкстры. Этот алгоритм вычисляет расстояние от фиксированной вершины v₀ до всех остальных вершин сети и находит кратчайший путь более эффективно, чем алгоритм Форда-Беллмана. Алгоритм заключается в последовательном вычислении расстояний сначала до ближайшей к v₀ вершине, затем до следующей ближайшей и т.д. ⁽¹⁾

Прежде, чем привести описание алгоритма, введем необходимые обозначения. Пусть N=(V,D,a) – сеть, v₀ – фиксированная вершина этой сети, v₁,…,v_k – остальные вершины. Для i=1,…,k расстояние d(v₀,v_i) обозначим через d(v_i). На множестве вершин введем двухместную функцию a(v,v’) следующим образом: