Потоки с ограничениями на дугах

Простые потоки

Пусть в данной сети N = (V,D,a) есть множество дуг, образующих простую цепь пли простой цикл в соответствующем неориентированном графе. Предположим, что мы ориентируем ребра, проходя эти простые цепи и циклы в одном из возможных направлений. Дуга С будет называться нормальной, если ее вновь введенная ориентация совпадает с исходной и обращенной (инвертированной) в противном случае.

Сеть N = (V, D) называется сетью с ограниченной пропускной способностью, если на D определены две функциии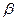, принимающие целочисленные значения, удовлетворяющие соотношению 0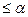(а)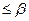(a) для всех аD, Целые числа (а) и 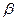(а) называются верхней и нижней границами пропускной способности дуги а и интерпретируются как максимально и минимально допустимая величина потока по каждой дуге. Если (а)=0 для всех аD, то 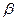(a) обычно называется пропускной способностью дуги а, а сеть называется транспортной сетью. Поток в сети называется допустимым тогда и только тогда, когда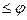 (а)(а)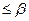(а) для всех аD.

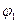Еслии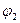— допустимые потоки, а —любой поток, ограниченный потокам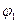и и 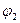, то очевидно, чтотакже является допустимым.