Задача о максимальном пути
Задача о максимальном пути формулируется следующим образом: в заданной сети N = (V,D,a) с выделенной вершиной v0 для каждой вершины v  V найти (v0,v)-путь, имеющий максимальную длину среди всех возможных (v0,v)-путей в сети N.
V найти (v0,v)-путь, имеющий максимальную длину среди всех возможных (v0,v)-путей в сети N.
Отметим, что имеет смысл решать эту задачу лишь в сетях, не содержащих контуров положительной длины. Рассмотрев тогда сеть, отличающуюся от исходной только изменением знаков весов дуг, получим сеть, в которой нет контуров отрицательной длины. Применяя к новой сети алгоритм Форда-Беллмана, можно построить кратчайшие (v0,v)-пути, которые будут путями максимальной длины в исходной сети.
Потоки в сетях (3)
Если мы припишем каждой дуге ориентированного графа поток некоторого вещества, граф становится удобной моделью при исследовании целого ряда проблем в транспорте, связи и других областях, связанных с действительным или воображаемым движением товаров, информации или людей.
Для данной сети N = (V,D,a) определим поток через N как функцию , сопоставляющую каждой дуге a из D неотрицательное действительное число
, сопоставляющую каждой дуге a из D неотрицательное действительное число 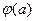 (называемое потоком через a) таким образом, что
(называемое потоком через a) таким образом, что 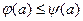 для любой дуги a; по отношению к сети N полустепень исхода и полустепень захода любой вершины (отличной от v и
для любой дуги a; по отношению к сети N полустепень исхода и полустепень захода любой вершины (отличной от v и 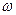 ) равны между собой. Рассуждая неформально, это означает, что поток через любую дугу не превосходит ее пропускной способности и что "полный поток", входящий в любую вершину (отличную от v и
) равны между собой. Рассуждая неформально, это означает, что поток через любую дугу не превосходит ее пропускной способности и что "полный поток", входящий в любую вершину (отличную от v и 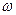 ), равен "полному потоку", выходящему из нее. Другим потоком является нулевой поток, при котором поток через каждую дугу равен нулю (любой другой поток называется ненулевым).
), равен "полному потоку", выходящему из нее. Другим потоком является нулевой поток, при котором поток через каждую дугу равен нулю (любой другой поток называется ненулевым).
Дуга a, для которой 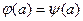 , называется насыщенной; остальные дуги называются ненасыщенными.
, называется насыщенной; остальные дуги называются ненасыщенными.
Направление потока определяется знаком  (а).
(а).
Вершины сети N обычно классифицируются по их воздействию на поток  (создают, поглощают или сохраняют поток). Чтобы формализовать классификацию, обозначим через v
(создают, поглощают или сохраняют поток). Чтобы формализовать классификацию, обозначим через v 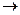 V множество дуг, для которых v является начальной вершиной, а через V
V множество дуг, для которых v является начальной вершиной, а через V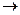 v —множество дуг, для которых v является конечной вершиной. Тогда целое число Q(v,
v —множество дуг, для которых v является конечной вершиной. Тогда целое число Q(v,  ), определяемое соотношением
), определяемое соотношением
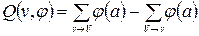
называется чистым потоком из v относительно  .
.
Сеть в целом сохраняет любой поток  в том смысле, что
в том смысле, что 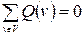 . Это хорошо видно из следующего выражения:
. Это хорошо видно из следующего выражения:
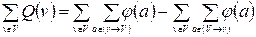 т.к. каждая дуга сети входит точно один раз в каждую двойную сумму.
т.к. каждая дуга сети входит точно один раз в каждую двойную сумму.
Пусть 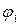 и
и 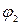 — потоки в одной и той же сети N=(V, D), и пусть р — целое число. Тогда для каждой
— потоки в одной и той же сети N=(V, D), и пусть р — целое число. Тогда для каждой
дуги а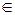 D потоки
D потоки 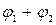 ,
, 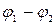 и
и 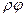 определяются с помощью следующих соотношений:
определяются с помощью следующих соотношений:
(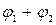 ) (а)=
) (а)=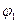 (а) +
(а) + 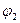 (а),
(а),
(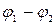 ) (а)=
) (а)= 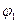 (а) -
(а) - 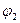 (а),
(а),
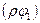 (а)=
(а)=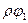 (а).
(а).
Легко видеть, что
Q(v,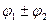 )=Q(v,
)=Q(v,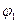 )
)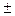 Q(v,
Q(v,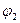 ),
),
Q(v,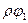 )=
)=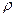 Q(v,
Q(v, 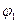 ).
).
Будем писать 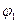 <
<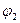 тогда и только тогда, когда
тогда и только тогда, когда 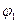 (а)<
(а)<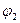 (а) для каждой а
(а) для каждой а D. Отношения между потоками
D. Отношения между потоками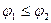 ,
, 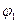 >
>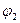 и
и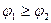 определяются аналогично. Говорят, что поток
определяются аналогично. Говорят, что поток  ограничен значениями
ограничен значениями 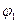 и
и 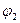 , если величина
, если величина  (а) заключена между
(а) заключена между 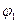 (a) и
(a) и 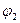 (а) для каждой дуги сети. Очевидно, что достаточным условием ограниченности потока
(а) для каждой дуги сети. Очевидно, что достаточным условием ограниченности потока потоками
потоками 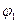 и
и 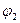 является выполнение одного из следующих соотношений:
является выполнение одного из следующих соотношений: 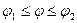 или
или  . Вообще, по некоторым дугам поток
. Вообще, по некоторым дугам поток  может быть ограничен сверху потоком
может быть ограничен сверху потоком 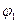 а по другим — потоком
а по другим — потоком 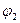 .
.
Потоки 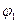 и
и 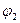 называются согласованными, если
называются согласованными, если 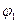 (а)*
(а)*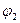 (а)
(а)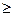 0 для каждой дуги а
0 для каждой дуги а V. Другими словами,
V. Другими словами, 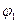 и
и 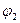 согласованы, если не существует дуг а, для которых
согласованы, если не существует дуг а, для которых 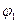 (а) и
(а) и 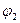 (а) отличны от нуля и противоположно направлены. Потоки {
(а) отличны от нуля и противоположно направлены. Потоки {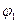
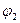 ,...,
,...,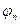 } в одной и той же сети называются совместно согласованными, если они попарно согласованы.
} в одной и той же сети называются совместно согласованными, если они попарно согласованы.
Связь понятий согласованных и ограниченных потоков устанавливается теоремой:
Теорема: Если S={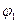 ,
, 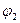 ,...,
,..., 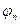 }—множество совместно согласованных потоков в сети N,
}—множество совместно согласованных потоков в сети N,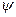 — произвольный поток в N и T
— произвольный поток в N и T S, то поток
S, то поток 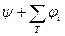 ограничен потоками
ограничен потоками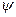 и
и 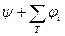 .
.
 2014-02-04
2014-02-04 716
716








