2014-02-04
1288
Шаг 1. Полагаем S=V\{ v0 }, d(vi)=a(v0,vi) для всех i=1,…,k.
Шаг 2. Если S=1, то выполнить шаг 4, иначе выбрать в S элемент v’, для которого величина d(v’) является наименьшей (среди всех элементов из S).
Шаг 3. Положить S=S\{ v’ }, d(v)=min{d(v), d(v ’)+a(v’,v)} для всех v 
S и перейти к шагу 2.
Шаг 4. Выдать d(v1),…,d(vk). Конец работы алгоритма.
Алгоритм осуществляет «итеративный» процесс нахождения расстояния d(vi) для i=1,…,k. Проследим, как это делается для сети N, изображенной на рис.1. Работа алгоритма будет иллюстрироваться заполнением таблицы 1.
При выполнении первого шага алгоритма величины d(vi) примут значения, которые указаны в нулевой строке таблицы. Из них точным является только d(v2), значения остальных величин завышены. На шаге 2 в качестве v’ выбирается вершина v2 (в таблице соответствующее значение набрано жирным шрифтом) и удаляется из S на шаге 3. На том же шаге уточняются предыдущие значения d(v) для v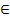
S (см. первую строку таблицы 1). На этом первый проход алгоритма заканчивается. На втором проходе в качестве v’ берется v5, удаляется из S и значения d(v) для v S снова уточняются. Результат уточнения отражен во второй строке таблицы. Когда множество S будет содержать только вершину
|
|
|
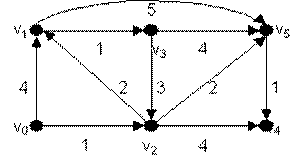
Рис. 1
Таблица 1
| Номер строки | d(v1) | d(v2) | d(v3) | d(v4) | d(v5) |
|
|
| |||
| - |
| ||||
| - |
| - | |||
| - | - | - | |||
| - | - | - | - |
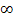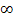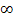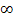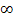V3 алгоритм заканчивает работу. Результат: d(v1)=3, d(v2)=1, d(v3)=4, d(v4)=4, d(v5)=3.
Поскольку на каждом проходе алгоритма число элементов множества S уменьшается на единицу, то алгоритм Дейкстры всегда заканчивает работу.
Случай бесконтурной сети (2)
В этом случае, так же как и в случае сетей с неотрицательными весами дуг, известен более эффективный алгоритм вычисления расстояний от фиксированной вершины до всех остальных, чем алгоритм Форда-Беллмана. В основе этого алгоритма лежат две леммы.
Лемма 1. В каждом бесконтурном орграфе имеется хотя бы одна вершина, полустепень исхода которой равна нулю.
Лемма 2. Вершины бесконтурного ориентированного графа можно перенумеровать так, что каждая дуга идет из вершины с меньшим номером в вершину с большим номером.
Орграфы с так пронумерованными вершинами иногда называют топологически отсортированными, а алгоритм, осуществляющий такую нумерацию вершин – алгоритмом топологической сортировки вершин.
При описании алгоритма вычисления расстояний в бесконтурной сети будем считать, что все вершины заданной сети топологически отсортированы. Расстояние будем вычислять от вершины v0.
Пусть vk – произвольная вершина заданной бесконтурной сети. Тогда любой (v0,vk)-путь проходит через вершины с меньшими чем k номерами. Из этого замечания следует, что для вычисления расстояний от v0 до всех остальных вершин сети достаточно последовательно вычислить расстояния от v0 до v1, затем от v0 до v2 и так далее. Пусть, как и раньше, d(v) обозначает расстояние от v0 до v. Тогда d(v0) = 0, и если d(vr) для всех r < k вычислено, то
|
|
|
d(vk) = min{d(vr) + d(vr,vk)| r = 1,2,…, k }.
