3.2.1. Определение предиката
Многие утверждения, имеющие форму высказываний, на самом деле таковыми не являются, так как содержат переменные, конкретные значения которых не указаны. Поскольку такое утверждение при одних значениях переменных может быть истинным, а при других — ложным, ему не может быть предписано истинностное значение. Такие утверждения, примерами которых являются
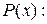 | 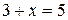 |
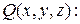 | 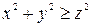 |
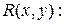 | 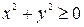 |
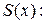 | 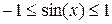 |
называются предикатами. Предикат с одной переменной называется одноместным предикатом. Предикат, имеющий две переменные, называется двуместным предикатом, а предикат, содержащий n переменных, называется n -местным предикатом. Предикат P(z) — одноместный, поскольку имеет одну переменную. Предикат Q(x,у,z) является трехместным предикатом. Предикаты становятся высказываниями, когда их переменным присваивается значение. Например,
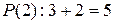
является высказыванием, и это высказывание истинно.
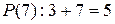
тоже является высказыванием, и это высказывание ложно.
Говорят, что набор значений переменных удовлетворяет предикату, если на этом наборе предикат принимает значение "истина", т.е. становится истинным высказыванием. Например, 2 удовлетворяет P (x), поскольку P (2) истинно, а 7 не удовлетворяет Р (х), поскольку P (7) ложно.
3.2.2. Кванторы. Их свойства и применение
3.2.2.1. Квантор всеобщности и квантор существования
Некоторые предикаты истинны для каждого возможного набора значений переменных, взятых из данного множества. Среди примеров, приведенных выше, S (x) — предикат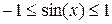 , где x принадлежит множеству действительных чисел. Тот факт, что для любого значения х
, где x принадлежит множеству действительных чисел. Тот факт, что для любого значения х
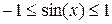
дает основание сказать, что
для любого x истинно S (x),
что символически изображается как
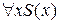
или
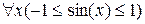 .
.
Символ 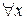 называется универсальным квантором, или квантором всеобщности, и читается "для любого x " или "для всех х ". Множество значений, которое может принимать z, называется универсом, или предметной областью. В частности, предметной областью может являться множество действительных чисел, множество целых чисел или другие подобные множества. Вообще говоря, истинность утверждения с квантором всеобщности зависит от предметной области. Например, высказывание
называется универсальным квантором, или квантором всеобщности, и читается "для любого x " или "для всех х ". Множество значений, которое может принимать z, называется универсом, или предметной областью. В частности, предметной областью может являться множество действительных чисел, множество целых чисел или другие подобные множества. Вообще говоря, истинность утверждения с квантором всеобщности зависит от предметной области. Например, высказывание
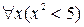
не истинно, если универсом (предметной областью) является множество целых чисел; однако, оно было бы истинным, если в качестве предметной области взять множество целых чисел, больших чем 2. Точно так же высказывание
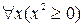
истинно, если предметная область — множество действительных чисел, но ложно, если предметная область содержит комплексное число i, т.к. 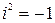 .
.
Квантифицированный предикат
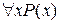
где 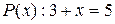 , не является истинным, если предметная область — множество целых чисел, потому что имеются значения x из этой области (например, х = 4) такие, что Р (х) ложно. Для истинности
, не является истинным, если предметная область — множество целых чисел, потому что имеются значения x из этой области (например, х = 4) такие, что Р (х) ложно. Для истинности 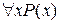 Р (х) должно быть истинным для каждого значения x из предметной области. Таким образом,
Р (х) должно быть истинным для каждого значения x из предметной области. Таким образом, 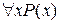 имеет конкретное истинностное значение, поэтому является высказыванием.
имеет конкретное истинностное значение, поэтому является высказыванием.
Для ясности будем иногда заключать квантор в скобки, записывая 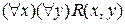 вместо
вместо 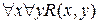 . Хотя
. Хотя 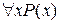 , вообще говоря, не истинно, P (x) истинно по крайней мере для одного значения х, а именно, х = 2. Поэтому существует х такой, что P (x) истинно. Символически это записывается как
, вообще говоря, не истинно, P (x) истинно по крайней мере для одного значения х, а именно, х = 2. Поэтому существует х такой, что P (x) истинно. Символически это записывается как
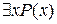 .
.
Символ 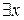 называется квантором существования. Здесь, как и в случае
называется квантором существования. Здесь, как и в случае 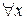 , выражение
, выражение 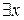 относится к значению х из предметной области.
относится к значению х из предметной области.
Высказывание
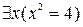
истинно, если предметной областью есть множество действительных чисел, т.к. 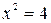 истинно для х = 2. Высказывание
истинно для х = 2. Высказывание
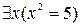
также истинно, если предметной областью есть множество действительных чисел; однако, оно не является истинным, если предметная область есть множество целых чисел, так как не существует целого числа, квадрат которого равен 5.
Чтобы предикат был высказыванием, все его переменные должны иметь конкретные значения или быть связаны соответствующим квантором. Например,
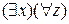
не является высказыванием, т.к. переменная у не связана никаким квантором.
Пример 5. Записать формулой логики предикатов предложение, отражающее транзитивное свойство делимости целых чисел.
Составное высказывание (предложение), являющееся формулировкой свойства транзитивности отношения делимости целых чисел:
«Если а делится на b и b делится на с, то а делится на с», состоит из трех простых высказываний D (a, b), D(b, с) и D(a, с). Следовательно, транзитивное свойство делимости можно записать в виде составного высказывания (логической формулы):
«Если D (a, b) и D(b, с), то D(a, с)» или:
(D (a, b) &D(b, с)) → D(a, с).
Пример 6. Пусть Р(х) – предикат "х – четное число", определенный на множестве М. Дать словесную формулировку высказыванию 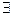 хР(х), определить его истинность.
хР(х), определить его истинность.
Исходный предикат Р(х) – "х – четное число" является переменным высказыванием: при подстановке конкретного числа вместо переменной х он превращается в простое высказывание, являющееся истинным или ложным, например при подстановке числа 5 превращается в высказывание "5 – четное число", являющееся ложным. Высказывание 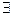 х Р(х) означает "в М существует четное число". Поскольку множество М, на котором задан предикат Р(х), не определено в условии (в таком случае говорят, что задача сформулирована не вполне корректно), доопределим М.
х Р(х) означает "в М существует четное число". Поскольку множество М, на котором задан предикат Р(х), не определено в условии (в таком случае говорят, что задача сформулирована не вполне корректно), доопределим М.
Пусть предикат Р(х) определен на множестве натуральных чисел N, т.е. х  N, тогда высказывание
N, тогда высказывание 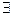 х Р(х) – истинно. В общем случае высказывание
х Р(х) – истинно. В общем случае высказывание 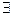 х Р(х) истинно на любом множестве М, содержащем хотя бы одно четное число, и ложно на любом множестве нечетных чисел.
х Р(х) истинно на любом множестве М, содержащем хотя бы одно четное число, и ложно на любом множестве нечетных чисел.
Пример 7. Записать предикатной формулой предложение "Любой человек имеет отца".
Для построения предикатной формулы используем два предиката "х – человек" и "у – отец х" и для удобства восприятия обозначим их соответственно: ЧЕЛОВЕК(х) и ОТЕЦ (у, х). Тогда предложение "Любой человек имеет отца" в предикатной форме имеет вид:
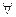 x (ЧЕЛОВЕК(х)→
x (ЧЕЛОВЕК(х)→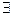 у ОТЕЦ (у, х)).
у ОТЕЦ (у, х)).
Заметим, что если предикат ОТЕЦ(у, х) определен на множестве людей, то выражение "любой человек имеет отца" можно записать проще:
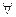 x
x 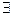 у ОТЕЦ (у, х).
у ОТЕЦ (у, х).
Пример 8. Определить истинность, ложность либо выполнимость следующих формул:
а) 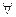 x P(x,y,x);
x P(x,y,x);
б) 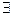 x P(x,y)→
x P(x,y)→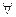 x P(x,y);
x P(x,y);
в) 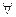 x (P(x)
x (P(x) 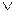
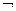 P(x)).
P(x)).
a) 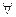 x P(x,y,x) – выполнимая формула. Действительно, формула выполнима в области N0 натуральных чисел с нулем (например, на модели N = (N0; S, П, Е) - арифметики натуральных чисел). Пусть, например, Р – предикат суммы S. Тогда для формулы
x P(x,y,x) – выполнимая формула. Действительно, формула выполнима в области N0 натуральных чисел с нулем (например, на модели N = (N0; S, П, Е) - арифметики натуральных чисел). Пусть, например, Р – предикат суммы S. Тогда для формулы 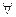 x S(x,y,x) существует подстановка константы вместо свободной переменной у=0, при которой эта формула становится истинной:
x S(x,y,x) существует подстановка константы вместо свободной переменной у=0, при которой эта формула становится истинной: 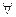 x S(x,0,x).
x S(x,0,x).
Таким образом, существует область N0, в которой формула 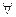 x P(x,y,x) выполнима, а значит, она просто выполнима.
x P(x,y,x) выполнима, а значит, она просто выполнима.
б) 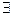 x P(x,y)→
x P(x,y)→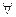 x P(x,y) – выполнимая формула. Она является тождественно-истинной (ТИ) формулой в области М1, состоящей из одного элемента, однако, не является ТИ-формулой во всех областях. Например, она лишь выполнима в области М2
x P(x,y) – выполнимая формула. Она является тождественно-истинной (ТИ) формулой в области М1, состоящей из одного элемента, однако, не является ТИ-формулой во всех областях. Например, она лишь выполнима в области М2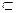 N0, являющейся конечным множеством натуральных чисел. Пусть P(x,y) – предикат порядка Q(x,y) – «x
N0, являющейся конечным множеством натуральных чисел. Пусть P(x,y) – предикат порядка Q(x,y) – «x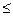 y». Тогда формула
y». Тогда формула 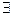 x Q(x,y)→
x Q(x,y)→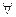 x Q(x,y) истинна при подстановке y= a max
x Q(x,y) истинна при подстановке y= a max M2:
M2: 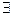 x Q(x, a max)→
x Q(x, a max)→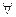 x Q(x, a max) и ложна при подстановке других констант a
x Q(x, a max) и ложна при подстановке других констант a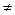 a max.
a max.
в) 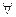 x (P(x)
x (P(x) 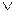
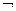 P(x)) – ТИ-формула, т.к. она истинна в любой области М. Действительно, при подстановке любой константы а любой области М предикат Р(а) либо истинен, т.е. Р(а)=1,
P(x)) – ТИ-формула, т.к. она истинна в любой области М. Действительно, при подстановке любой константы а любой области М предикат Р(а) либо истинен, т.е. Р(а)=1, 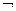 Р(а)=0 и P(а)
Р(а)=0 и P(а) 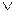
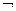 P(а)=1
P(а)=1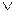 0=1 (истинно), либо ложен, т.е. Р(а)=0,
0=1 (истинно), либо ложен, т.е. Р(а)=0, 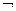 Р(а)=1 и P(а)
Р(а)=1 и P(а) 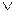
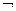 P(а)=0
P(а)=0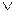 1=1 (истинно).
1=1 (истинно).
 2014-02-04
2014-02-04 9011
9011








