2014-02-04
1784
Сумма потоков через дуги, инцидентные v, равна сумме потоков через дуги, инцидентные w; эта сумма называется величиной потока. Будем в первую очередь интересоваться потоками, имеющими наибольшую возможную величину, — так называемыми максимальными потоками. В общем случае сеть может иметь несколько различных максимальных потоков, однако их величины должны совпадать.(4)
Изучение максимальных потоков через сеть N = (V,D,a) тесно связано с понятием разреза, т.е. такого множества A дуг орграфа D, которое обладает тем свойством, что любая простая цепь из v в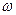 
проходит через дугу, принадлежащую A. Пропускной способностью разреза называется сумма пропускных способностей принадлежащих ему дуг. Разрезы, обладающие наименьшей возможной пропускной способностью, называются минимальными разрезами.
Величина любого потока не превышает пропускной способности любого разреза, и, следовательно, величина любого максимального потока не превышает пропускной способности любого минимального разреза. Однако сразу не ясно, что два последних числа всегда равны между собой; Этот результат был получен американскими математиками Фордом и Фалкерсоном в 1955 году и назван теоремой о максимальном потоке и минимальном разрезе.
|
|
|
Теорема (о максимальном потоке и минимальном разрезе). Во всякой сети величина любого максимального потока равна пропускной способности любого минимального разреза.
Теорема о максимальном потоке и минимальном разрезе позволяет проверять, максимален данный поток или нет, но только для достаточно простых сетей. Разумеется, на практике приходится иметь дело с большими и сложными сетями, и в общем случае трудно найти максимальный поток простым подбором. Опишем один алгоритм нахождения максимального потока в любой сети с целочисленными пропускными способностями.
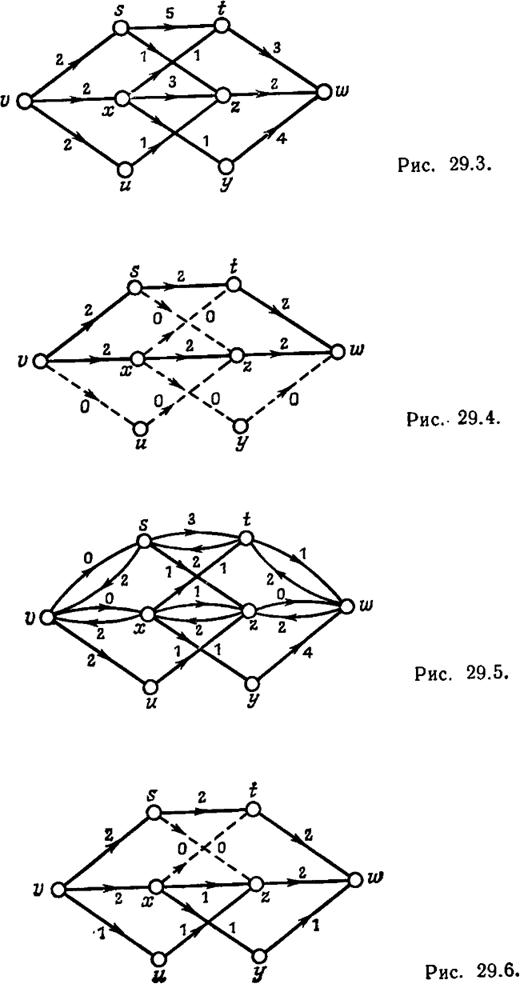
Шаг 1. Сначала подберем поток
, обладающий ненулевой величиной (если такой поток существует). Например, если N – сеть, представленная на рис. 29.3, то подходящим будет поток, изображенный на рис. 29.4. Стоит отметить, что чем больше величина выбранного нами начального потока , тем проще будут последующие шаги.
Шаг 2. Исходя из N, строим новую сеть N’ путем изменения направления потока на противоположное. Более точно, любая дуга a, для которой(a) = 0, остается в N’ со своей первоначальной пропускной способностью, а любая дуга a, для которой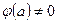 
, заменяется дугой a с пропускной способностью 
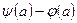и противоположно направленной дугой с пропускной способностью (a). Сеть N’ в нашем примере показана на рис. 29.5. Вершина v уже не является источником,а 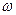– стоком.
Шаг 3. Если в сети N’ мы сможем найти ненулевой поток из v в, то его можно добавить к первоначальному потокуи получить в N новый поток
’большей величины. Теперь можно повторить шаг 2, используя при построении сети N’ новый поток’ вместо. Повторяя эту процедуру, мы в конце концов придем к сети N’, не содержащей ненулевых потоков; тогда соответствующий потокбудет максимальным потоком. Например, на рис. 29.5 существует ненулевой поток, в котором потоки через дуги (v,u), (u,z), (z,x), (x,y) и (y,) равны единице, а потоки через остальные дуги равны нулю. Добавляя этот поток к потоку на рис. 29.4, получим поток, изображенный на рис. 29.6; повторяя шаг 2, легко показать, что это и есть максимальный поток.
|
|
|
Используемая литература:
(1) https://pgap.chat.ru/zap/zap264.htm#0
(2) Асанов М.О., Баранский В.А., Расин В.В. Дискретная математика: графы матроиды, алгоритмы
(3) Басакер Р., Саати Т. Конечные графы и сети.
(4) Уилсон Р. Введение в теорию графов
