Введение в математическую логику
Логика, созданная как наука Аристотелем (384–322 г. до н.э.), на протяжении столетий использовалась для развития многих областей знания, включая теологию, философию, математику.
Она – тот фундамент, на котором построено все здание математики. По сути, логика — это наука о рассуждениях, которая позволяет определить истинность или ложность того или иного математического утверждения, исходя из совокупности первичных предположений, называемых аксиомами. Логика применяется также в информатике для построения компьютерных программ и доказательства их корректности. Понятия, методы и средства логики лежат в основе современных информационных технологий. Одна из основных целей этой работы — изложить основы математической логики, показать, как она используется в информатике, и разработать методы анализа и доказательства математических утверждений.
Логические представления - описание исследуемой системы, процесса, явления в виде совокупности сложных высказываний, составленных из простых (элементарных) высказываний и логических связок между ними. Логические представления и их составляющие характеризуются определенными свойствами и набором допустимых преобразований над ними (операций, правил вывода и т.п.), реализующих разработанные в формальной (математической) логике правильные методы рассуждений — законы логики.
Понятие высказывания
Высказывание — это утверждение или повествовательное предложение, о котором можно сказать, что оно истинно или ложно. Иными словами, утверждение об истинности или ложности высказывания должно иметь смысл. Истинность или ложность, приписываемые некоторому утверждению, называются его значением истинности, или истинностным значением.
Например, высказывания Дважды два четыре и Город Челябинск находится в азиатской части России истинные, а высказывания Три больше пяти и Река Дон в настоящее время впадает в Каспийское море ложны, так как не соответствуют действительности. Истинные высказывания принято обозначать T (true) или И (истина), а ложные, соответственно, F (false) или Л (ложь). В информатике истинность принято обозначать 1 (двоичная единица), а ложность – 0 (двоичный ноль).
Вот примеры предложений, не являющихся высказываниями:
Кто вы? (вопрос),
Прочтите эту главу до следующего занятия (приказ или восклицание),
Это утверждение ложно (внутренне противоречивое утверждение),
Площадь отрезка меньше длины куба (нельзя сказать истинно это предложение или ложно, т.к. не имеет смысла).
Мы будем обозначать высказывания буквами латинского алфавита р, q, r, Например, р может обозначать утверждение Завтра будет дождь, а q — утверждение Квадрат целого числа есть число положительное.
Логические связки
В обыденной речи для образования сложного предложения из простых используются связки — особые части речи, соединяющие отдельные предложения. Наиболее часто употребляются связки и, или, не, если... то, только если, и тогда и только тогда. В отличие от обыденной речи, в логике смысл таких связок должен быть определен однозначно. Истинность сложного высказывания однозначно определяется истинностью или ложностью составляющих его частей. Высказывание, не содержащее связок, называется простым. Высказывание, содержащее связки, называется сложным. Логические связки также называют логическими операциями над высказываниями.
Пусть р и q обозначают высказывания
р: Джейн водит автомобиль,
q: У Боба русые волосы.
Сложное высказывание
Джейн водит автомобиль и у Боба русые волосы состоит из двух частей, объединенных связкой и. Это высказывание может быть символически записано в виде
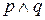 .
.
где символ  обозначает слово и на языке символических выражений. Выражение
обозначает слово и на языке символических выражений. Выражение 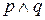 называется конъюнкцией высказываний р и q.
называется конъюнкцией высказываний р и q.
Встречаются также следующие варианты записи конъюнкции:
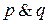
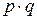
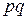
Точно так же высказывание
Джейн водит автомобиль или у Боба русые волосы.
символически выражается как

где  обозначает слово или в переводе на символический язык. Выражение
обозначает слово или в переводе на символический язык. Выражение  называется дизъюнкцией высказываний р и q.
называется дизъюнкцией высказываний р и q.
Опровержение, или отрицание высказывания p обозначается через

или
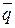
или
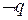
Таким образом, если р есть высказывание Джейн водит автомобиль, то 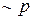 – это утверждение Джейн не водит автомобиль.
– это утверждение Джейн не водит автомобиль.
Если r есть высказывание Джо нравится информатика, то Джейн не водит автомобиль и у Боба русые волосы или Джо любит информатику символически запишется как
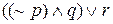 .
.
И наоборот, выражение
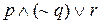
это символическая форма записи высказывания Джейн водит автомобиль, у Боба волосы не русые и Джо нравится информатика.
Рассмотрим выражение 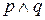 . Если некто говорит: " Джейн водит автомобиль и у Боба русые волосы", то мы, естественно, представляем себе Джейн за рулем автомобиля и русоволосого Боба. В любой другой ситуации (например, если Боб не русоволос или Джейн не водит автомобиль) мы скажем, что говорящий не прав.
. Если некто говорит: " Джейн водит автомобиль и у Боба русые волосы", то мы, естественно, представляем себе Джейн за рулем автомобиля и русоволосого Боба. В любой другой ситуации (например, если Боб не русоволос или Джейн не водит автомобиль) мы скажем, что говорящий не прав.
Возможны четыре случая, которые нам необходимо рассмотреть. Высказывание р может быть истинным (Т) или ложным (F) и независимо от того, какое истинностное значение принимает р, высказывание q может также быть истинным (Т) или ложным (F). Таблица истинности перечисляет все возможные комбинации истинности и ложности сложных высказываний.
| Случай | p | q | 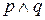 |
| T | T | T | |
| T | F | F | |
| F | T | F | |
| F | F | F |
Итак, конъюнкция 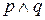 истинна тогда и только тогда, когда истинны оба высказывания p и q, то есть в случае 1.
истинна тогда и только тогда, когда истинны оба высказывания p и q, то есть в случае 1.
Точно так же рассмотрим высказывание Джейн водит автомобиль или у Боба русые волосы, которое символически выражается как  . Если некто скажет: "Джейн водит автомобиль или у Боба русые волосы", то он будет не прав только тогда, когда Джейн не сможет управлять автомобилем, а Боб не будет русоволосым. Для того чтобы все высказывание было истинным, достаточно, чтобы одна из двух составляющих его компонент была истинной. Поэтому
. Если некто скажет: "Джейн водит автомобиль или у Боба русые волосы", то он будет не прав только тогда, когда Джейн не сможет управлять автомобилем, а Боб не будет русоволосым. Для того чтобы все высказывание было истинным, достаточно, чтобы одна из двух составляющих его компонент была истинной. Поэтому  имеет таблицу истинности
имеет таблицу истинности
| Случай | p | q |  |
| T | T | T | |
| T | F | T | |
| F | T | T | |
| F | F | F |
Дизъюнкция  ложна только в случае 4, когда оба р и q ложны.
ложна только в случае 4, когда оба р и q ложны.
Таблица истинности для отрицания 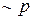 имеет вид
имеет вид
| Случай | p | 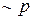 |
| T | F | |
| F | T |
Истинностное значение 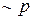 всегда противоположно истинностному значению р. В таблицах истинности отрицание всегда оценивается первым, если только за знаком отрицания не следует высказывание, заключенное в скобки. Поэтому
всегда противоположно истинностному значению р. В таблицах истинности отрицание всегда оценивается первым, если только за знаком отрицания не следует высказывание, заключенное в скобки. Поэтому 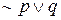 интерпретируется как
интерпретируется как  , так что отрицание применяется только к р. Если мы хотим отрицать все высказывание
, так что отрицание применяется только к р. Если мы хотим отрицать все высказывание , то это записывается как
, то это записывается как 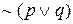 .
.
Символы  и
и  называют бинарными связками, так как они связывают два высказывания. Символ ~ является унарной связкой, так как применяется только к одному высказыванию.
называют бинарными связками, так как они связывают два высказывания. Символ ~ является унарной связкой, так как применяется только к одному высказыванию.
Еще одна бинарная связка – это исключающее или, которое обозначается через 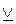 . Высказывание
. Высказывание 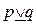 истинно, когда истинно p или q, но не оба одновременно. Эта связка имеет таблицу истинности
истинно, когда истинно p или q, но не оба одновременно. Эта связка имеет таблицу истинности
| Случай | p | q |  |
| T | T | F | |
| T | F | T | |
| F | T | T | |
| F | F | F |
Используя слово или, мы можем иметь в виду исключающее или. Например, когда мы говорим, что р — либо истина, либо ложь, то, естественно, предполагаем, что это не выполняется одновременно. В логике исключающее или используется довольно редко, и в дальнейшем мы, как правило, будем обходиться без него.
Рассмотрим высказывание
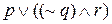 ,
,
где скобки использованы, чтобы показать, какие именно высказывания являются компонентами каждой связки.
Таблица истинности дает возможность однозначно указать те ситуации, когда высказывание 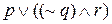 является истинным; при этом мы должны быть уверены, что учтены все случаи. Поскольку сложное высказывание содержит три основных высказывания р, q и r, то возможны восемь случаев
является истинным; при этом мы должны быть уверены, что учтены все случаи. Поскольку сложное высказывание содержит три основных высказывания р, q и r, то возможны восемь случаев
| Случай | p | q | r |  | 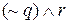 | 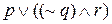 |
| T | T | T | F | F | T | |
| T | T | F | F | F | T | |
| T | F | T | T | T | T | |
| T | F | F | T | F | T | |
| F | T | T | F | F | F | |
| F | T | F | F | F | F | |
| F | F | T | T | T | T | |
| F | F | F | T | F | F |
При нахождении значений истинности для столбца 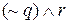 мы используем столбцы для
мы используем столбцы для  и r, а также таблицу истинности для
и r, а также таблицу истинности для  . Таблица истинности для
. Таблица истинности для  показывает, что высказывание
показывает, что высказывание 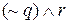 истинно лишь в том случае, когда истинны оба высказывания
истинно лишь в том случае, когда истинны оба высказывания  и r. Это имеет место лишь в случаях 3 и 7.
и r. Это имеет место лишь в случаях 3 и 7.
Заметим, что при определении значений истинности для столбца 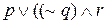 играет роль только истинность высказываний p и
играет роль только истинность высказываний p и 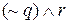 . Таблица истинности для
. Таблица истинности для  показывает, что единственный случай, когда высказывание, образованное с помощью связки или, ложно, — это случай, когда ложны обе части этого высказывания. Такая ситуация имеет место только в случаях 5, 6 и 8.
показывает, что единственный случай, когда высказывание, образованное с помощью связки или, ложно, — это случай, когда ложны обе части этого высказывания. Такая ситуация имеет место только в случаях 5, 6 и 8.
Другой, эквивалентный способ построения таблицы истинности состоит в том, чтобы записывать истинностные значения выражения под связкой. Снова рассмотрим выражение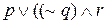 . Сначала мы записываем истинностные значения под переменными р, q и r. Единицы под столбцами истинностных значений указывают на то, что этим столбцам истинностные значения присваиваются в первую очередь. В общем случае число под столбцом будет показывать номер шага, на котором производятся вычисления соответствующих истинностных значений. Затем мы записываем под символом ~ истинностные значения высказывания
. Сначала мы записываем истинностные значения под переменными р, q и r. Единицы под столбцами истинностных значений указывают на то, что этим столбцам истинностные значения присваиваются в первую очередь. В общем случае число под столбцом будет показывать номер шага, на котором производятся вычисления соответствующих истинностных значений. Затем мы записываем под символом ~ истинностные значения высказывания  . Далее записываем истинностные значения
. Далее записываем истинностные значения 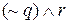 под символом
под символом  . Наконец, записываем значения высказывания
. Наконец, записываем значения высказывания 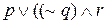 под символом
под символом  .
.
| Случай | p | q | r | p |  | ((~ | q) |  | r |
| T | T | T | T | T | F | T | F | T | |
| T | T | F | T | T | F | T | F | F | |
| T | F | T | T | T | T | F | T | T | |
| T | F | F | T | T | F | F | F | F | |
| F | T | T | F | F | F | T | F | T | |
| F | T | F | F | F | F | T | F | F | |
| F | F | T | F | T | T | F | T | T | |
| F | F | F | F | F | F | F | F | F | |
1.1.3. Условные высказывания
Допустим, некто утверждает, что если случится одно событие, то случится и другое. Предположим, отец говорит сыну: " Если в этом семестре ты сдашь все экзамены на «отлично», я куплю тебе машину ". Заметьте, что высказывание имеет вид: если р, то q, где р — высказывание В этом семестре ты сдашь все экзамены на «отлично», а q — высказывание Я куплю тебе машину. Сложное высказывание мы обозначим символически через  . Спрашивается, при каких условиях отец говорит правду? Предположим, высказывания р и q истинны. В этом случае счастливый студент получает отличные оценки по всем предметам, и приятно удивленный отец покупает ему машину. Естественно, ни у кого не вызывает сомнения тот факт, что высказывание отца было истинным. Однако существуют еще три других случая, которые необходимо рассмотреть. Допустим, студент действительно добился отличных результатов, а отец не купил ему машину.
. Спрашивается, при каких условиях отец говорит правду? Предположим, высказывания р и q истинны. В этом случае счастливый студент получает отличные оценки по всем предметам, и приятно удивленный отец покупает ему машину. Естественно, ни у кого не вызывает сомнения тот факт, что высказывание отца было истинным. Однако существуют еще три других случая, которые необходимо рассмотреть. Допустим, студент действительно добился отличных результатов, а отец не купил ему машину.
Самое мягкое, что можно сказать об отце в таком случае, — это то, что он солгал. Следовательно, если р истинно, а q ложно, то  ложно. Допустим теперь, что студент не получил положительные оценки, но отец тем не менее купил ему машину. В этом случае отец предстает очень щедрым, но его никак нельзя назвать лжецом. Следовательно, если р ложно и q истинно, то высказывание если р, то q (т.е.
ложно. Допустим теперь, что студент не получил положительные оценки, но отец тем не менее купил ему машину. В этом случае отец предстает очень щедрым, но его никак нельзя назвать лжецом. Следовательно, если р ложно и q истинно, то высказывание если р, то q (т.е.  ) истинно. Наконец, предположим, что студент не добился отличных результатов, и отец не купил ему машину.
) истинно. Наконец, предположим, что студент не добился отличных результатов, и отец не купил ему машину.
Поскольку студент не выполнил свою часть соглашения, отец тоже свободен от обязательств. Таким образом, если р и q ложны, то  считается истинным. Итак, единственный случай, когда отец солгал, — это когда он дал обещание и не выполнил его.
считается истинным. Итак, единственный случай, когда отец солгал, — это когда он дал обещание и не выполнил его.
Таким образом, таблица истинности для высказывания  имеет вид
имеет вид
| Случай | p | q |  |
| T | T | T | |
| T | F | F | |
| F | T | T | |
| F | F | T |
Символ 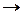 называется импликацией, или условной связкой.
называется импликацией, или условной связкой.
Может показаться, что  носит характер причинно-следственной связи, но это не является необходимым. Чтобы увидеть отсутствие причины и следствия в импликации, вернемся к примеру, в котором р есть высказывание Джейн управляет автомобилем, а q — утверждение У Боба русые волосы. Тогда высказывание Если Джейн управляет автомобилем, то у Боба русые волосы запишется как
носит характер причинно-следственной связи, но это не является необходимым. Чтобы увидеть отсутствие причины и следствия в импликации, вернемся к примеру, в котором р есть высказывание Джейн управляет автомобилем, а q — утверждение У Боба русые волосы. Тогда высказывание Если Джейн управляет автомобилем, то у Боба русые волосы запишется как
если p, то q или как  .
.
То, что Джейн управляет автомобилем, никак причинно не связано с тем, что Боб русоволосый. Однако нужно помнить, что истинность или ложность бинарного сложного высказывания зависит только от истинности составляющих его частей и не зависит от наличия или отсутствия между ними какой-либо связи.
Рассмотрим следующий пример. Требуется найти таблицу истинности для выражения
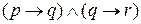 .
.
Используя таблицу истинности для 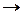 , приведенную выше, построим сначала таблицы истинности для
, приведенную выше, построим сначала таблицы истинности для  и
и 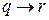 , учитывая, что импликация ложна только в случае, когда
, учитывая, что импликация ложна только в случае, когда 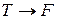 .
.
Теперь используем таблицу для  , чтобы получить для высказывания
, чтобы получить для высказывания
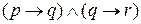
таблицу истинности
| Случай | p | q | r | (p | 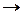 | q) |  | (q | 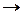 | r) |
| T | T | T | T | T | T | T | T | T | T | |
| T | T | F | T | T | T | F | T | F | F | |
| T | F | T | T | F | F | F | F | T | T | |
| T | F | F | T | F | F | F | F | T | F | |
| F | T | T | F | T | T | T | T | T | T | |
| F | T | F | F | T | T | F | T | T | F | |
| F | F | T | F | T | F | T | F | F | T | |
| F | F | F | F | T | F | T | F | T | F | |
| * |
Высказывание вида 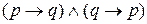 обозначается через
обозначается через 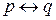 . Символ
. Символ 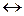 называется эквиваленцией. Эквиваленция также иногда обозначается как
называется эквиваленцией. Эквиваленция также иногда обозначается как 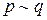 (не следует путать с унарной операцией отрицания).
(не следует путать с унарной операцией отрицания).
Очевидно, таблица истинности для 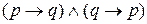 определяет таблицу истинности для
определяет таблицу истинности для 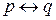 . Непосредственно из определения вытекает, что эквиваленция истинна только в случае, когда р и q имеют одинаковые истинностные значения.
. Непосредственно из определения вытекает, что эквиваленция истинна только в случае, когда р и q имеют одинаковые истинностные значения.
Может возникнуть вопрос о том, как интерпретировать такие выражения, как 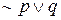 ,
, 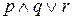 ,
, 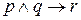 и
и 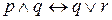 , в которых отсутствуют скобки. Во избежание неоднозначности лучше всегда использовать скобки. Однако здесь, как и в алгебре, имеется приоритет выполнения операций. Операции выполняются в следующей последовательности: ~,
, в которых отсутствуют скобки. Во избежание неоднозначности лучше всегда использовать скобки. Однако здесь, как и в алгебре, имеется приоритет выполнения операций. Операции выполняются в следующей последовательности: ~,  ,
,  ,
, 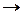 ,
, 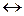 . Поэтому указанные выражения можно интерпретировать как
. Поэтому указанные выражения можно интерпретировать как  ,
, 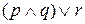 ,
, 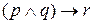 и
и 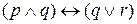 .
.
Эквивалентные высказывания
Особый интерес представляют сложные высказывания, имеющие различное строение, но являющиеся истинными в одних и тех же случаях. Такие высказывания называются логически эквивалентными. Эквивалентность двух высказываний легко установить посредством сравнения их таблиц истинности.
Рассмотрим сложные высказывания 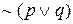 и
и  . Построим таблицы истинности для обоих высказываний
. Построим таблицы истинности для обоих высказываний
| Случай | p | q | ~ | 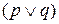 | 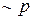 |  |  |
| T | T | F | T | F | F | F | |
| T | F | F | T | F | F | T | |
| F | T | F | T | T | F | F | |
| F | F | T | F | T | T | T | |
| * | # |
Итак, во всех четырех строках истинностные значения для 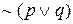 (обозначенные *) и для
(обозначенные *) и для  (обозначенные #) совпадают. Это означает, что два рассматриваемых высказывания логически эквивалентны, т.е.
(обозначенные #) совпадают. Это означает, что два рассматриваемых высказывания логически эквивалентны, т.е.
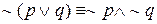
Эквивалентность — очень полезное свойство; используя его, можно строить отрицание высказываний с "или", осуществляя отрицание каждой из его частей и меняя "или" на "и".
С условным высказыванием — импликацией  связаны еще три типа высказываний: конверсия, инверсия и контрапозиция высказывания
связаны еще три типа высказываний: конверсия, инверсия и контрапозиция высказывания  . Они определяются следующим образом:
. Они определяются следующим образом:
 импликация
импликация
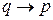 конверсия высказывания
конверсия высказывания 
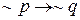 инверсия высказывания
инверсия высказывания 
 контрапозиция высказывания
контрапозиция высказывания 
Пусть дано высказывание-импликация Если он играет в футбол, то он популярен. Для этой импликации имеем:
конверсия: Если он популярен, то он играет в футбол
инверсия: Если он не играет в футбол, то он не популярен
контрапозиция: Если он не популярен, то он не играет в футбол
Важно понимать, что высказывания Если он живет в Детройте, то Боб навестит его и Боб навестит его, если он живет в Детройте по сути являются одним и тем же высказыванием. Однако высказывание Если Боб навестит его, то он живет в Детройте не совпадает с предыдущими высказываниями. Не важен порядок, в котором р и q присутствуют в предложении, а важно, какая часть предложения является частью "если", а какая часть является частью "то". Может показаться, что при замене если р, то q на q, если р получается конверсия, но с логической точки зрения последнее высказывание совпадает с исходным.
Эквивалентность и контрапозиция условных высказываний имеют в математике большое значение. Зачастую гораздо легче доказать теорему от противного, чем дать ее прямое доказательство. Используя эквивалентность импликации и ее контрапозиции, нетрудно показать, что конверсия и инверсия импликации имеют одну и ту же таблицу истинности. В то же время импликация и ее конверсия (или инверсия) имеют различные таблицы истинности.
Используя таблицы истинности, можно доказать следующие логические эквивалентности:
а) Законы идемпотентности
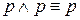
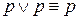
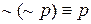
в) Законы де Моргана
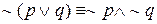
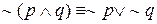
г) Свойства коммутативности
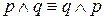
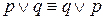
д) Свойства ассоциативности
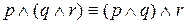
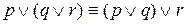
 2014-02-04
2014-02-04 12275
12275
