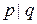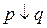З) Другие полезные свойства

Ж) Закон контрапозиции

E) Свойства дистрибутивности

.

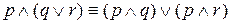
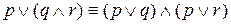
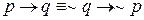
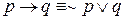
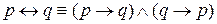Отметим, что благодаря свойству ассоциативности высказывания 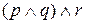и 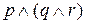могут быть записаны в виде 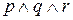. Аналогично, 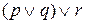и 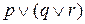можно записать просто как .

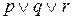Условные высказывания могут выражаться в виде различных языковых конструкций, но символически все они записываются как . Вот несколько примеров таких конструкций:

Если р, то q.

р достаточно для q.

р является достаточным условием для q.

q необходимо для р.

q является необходимым условием для р.

р, только если q (или: только если q то р).

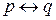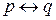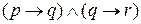Вернемся к рассмотрению логической связки . Поскольку высказывания вида и логически эквивалентны, то 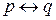означает то же, что и р тогда и только тогда, когда q, или р если и только если q.

Следующие языковые конструкции, выражающие эквиваленцию высказываний 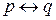, равносильны:

p если и итолько если q.

p необходимо и достаточно для q.

p есть необходимое и достаточное условие для q.

3.1.2. Аксиоматические системы

3.1.2.1. Умозаключения

Математики в большинстве своем имеют дело с теоремами и их доказательствами. Теоремы представляют собой "истинные" утверждения относительно рассматриваемых математических систем. Например, утверждение

Гипотенуза прямоугольного треугольника длиннее любого из катетов

– это известная из геометрии теорема Евклида. Это утверждение считается истинным, поскольку оно "выводимо" из ранее принятых или выведенных истин геометрии Евклида.

Математическая система начинается с неопределяемых понятий и утверждений, точно описывающих фундаментальные характеристики или истинные утверждения относительно этих понятий, которые математики используют для образования системы. Эти фундаментальные характеристики называются аксиомами или постулатами. Утверждения, выведенные (доказанные) только на основе этих фундаментальных свойств (аксиом и постулатов) и ранее доказанных утверждений с помощью логических правил, называются теоремами.

Таким образом, в математических системах вся информация, необходимая для доказательства теоремы, должна содержаться в аксиомах и ранее доказанных теоремах. Развивая конкретный раздел математики, можно не включать в него все аксиомы и доказанные теоремы. Вместо этого можно принять доказанные теоремы в качестве аксиом.

Важно, что логические правила, которые используются для вывода новых теорем из аксиом, постулатов и ранее доказанных в данной системе теорем, не порождают в качестве "теорем" ложные высказывания. Эти логические правила называются правилами вывода. Умозаключение состоит из совокупности утверждений, называемых гипотезами, или посылками, и утверждения, называемого заключением. Правильным умозаключением называется такое умозаключение, заключение которого истинно всякий раз, когда истинны его гипотезы. Правила вывода выбираются так, чтобы они были правильными умозаключениями.

Умозаключения часто представляют в виде

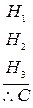		гипотезы
заключение

Символ 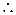означает "следовательно". Гипотезы представляют собой перечень одного или более высказываний, или посылок. Умозаключение правильно, если всякий раз, когда 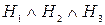истинно, истинно и С.

Правильность умозаключения можно проверить двумя способами. Во-первых, мы можем построить таблицу истинности и показать, что всякий раз, когда гипотезы истинны, истинно и заключение. Во-вторых, мы можем использовать таблицы истинности для обоснования правил вывода, а затем использовать правила вывода для доказательства справедливости заключения. Длинные умозаключения, как правило, проще обосновывать при помощи правил вывода.

Рассмотрим умозаключение

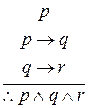
Таблицы истинности для посылок и заключения имеют следующий вид.

Случай	p	q	r	p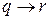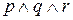
	T	T	T	T	T	T	T
	T	T	F	T	T	F	F
	T	F	T	T	F	T	F
	T	F	F	T	F	T	F
	F	T	T	F	T	T	T
	F	T	F	F	T	F	F
	F	F	T	F	T	T	T
	F	F	F	F	T	T	T
							*

Заметим, что, когда истинны все посылки (что имеет место в случае 1): истинным также является и заключение, а само умозаключение является правильным.

3.1.3. Полнота в логике высказываний

3.1.3.1. Эквивалентные замены логических связок

Рассмотрим вопрос о минимальном количестве логических связок, необходимых для выражения любого высказывания, образованного с помощью определенных нами выше логических связок. Известно, что 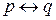можно выразить как 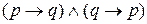, так что использовать 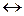удобно, но не необходимо. К тому же 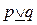эквивалентно .

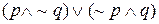Также 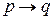эквивалентно 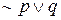, поэтому нет необходимости использовать 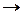, если применяется ~ и . Кроме того, 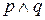эквивалентно и эквивалентно 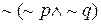. Следовательно, любое высказывание может быть выражено через пару связок ~ и или ~ и , причем в любом случае необходимы обе связки. Однако существуют две связки, обладающие тем свойством, что любое высказывание может быть выражено с использованием только одной из них. Эти связки: | – так называемый штрих Шеффера и 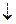— так называемая стрелка Пирса (стрелка Пирса также иногда обозначается как 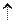). Свои названия эти связки получили в честь математиков Г.Шеффера и Ч.Пирса. Этим связкам соответствуют таблицы истинности

Случай p q   T T F   T F T   F T T   F F T

Случай p q   T T F   T F F   F T F   F F T

Для того, чтобы показать, что любую связку можно заменить одной лишь связкой | или только связкой 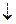, достаточно показать это для пар связок ~ и или ~ и , поскольку возможность выразить любую связку одной из этих пар уже показана. Эквивалентность и 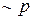устанавливается при помощи следующей таблицы истинности:

Случай	p	p	|	p
	T	T	F	T
	F	F	T	F
			*

Аналогично, при помощи таблиц истины, доказывается.

,

.

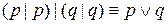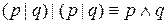Также, если показать, что ~ и или ~ и можно выразить, используя только 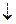, тогда и любую связку можно выразить, используя лишь 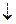. Аналогично предыдущему случаю доказательству 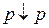эквивалентно 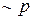. Также доказывается

,

.

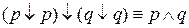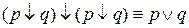Также заметим, что

.

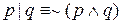
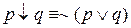Поэтому в дальнейшем связка | будет называться не-и или и-не, а связка 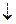будет называться не-или или или-не.

Пример 1. Представить логическими формулами следу­ющие высказывания:

1. "Сегодня понедельник или вторник".

2. "Идет дождь или снег".

3. "Если идет дождь, то крыши мокрые. Дождя нет, а кры­ши мокрые".

4. "Что в лоб, что по лбу".

1. Составное (сложное) высказывание "Сегодня поне­дельник или вторник" состоит из двух простых:

А – «Сегодня понедельник»;

В – «Сегодня вторник».

Высказывания А, В соединены связкой "или" очевидно в разделительном смысле, т.е. - 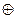. Таким образом, данное выс­казывание представимо логической формулой:

А 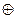В

2. Высказывание "Идет дождь или снег" состоит из двух простых:

А – «Идет дождь»;

В – «Идет снег».

Но в отличие от предыдущего о связка ''или'' использована здесь не в разделительном смысле, поэтому логическая формула имеет вид:

А 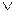В

3. Сложное высказывание «Если идет дождь, то крыши мокрые. Дождя нет, а кры­ши мокрые» включает два простых высказывания:

А – «Идет дождь»,

В – «Крыши мокрые».

В первом высказывании «Если идет дождь, то крыши мокрые» высказывания А и В соединены связкой следования:

А→В

Во втором «Дождя нет, а кры­ши мокрые» высказывания А и В связаны связкой «и», кроме того первое следует взять с отрицанием:

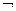А&B

Остается объединить два полученных выше высказывания в одно связкой «и»

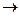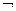(АВ)&(А&B)

4. Высказывание «Что в лоб, что по лбу» содержит два простых:

А – «В лоб»,

В – «По лбу»,

Представимо формулой:

А~В

Пример 2. Записать логическими формулами следующие сложные высказывания:

1. "Если допоздна работаешь с компьютером и при этом пьешь много кофе, то утром просыпаешься в дурном распо­ложении духа или с головной болью".

2. "Если социологические исследования показывают, что потребитель отдает предпочтение удобству и многообразию выбора, то фирме следует сделать упор на усовершенствова­ние товара или увеличение многообразия новых форм".

1. Первое составное высказывание состоит из следую­щих простых:

Х – "Допоздна работаешь с компьютером".

Y – "Пьешь много кофе".

Z – "Утром встаешь в дурном расположении духа".

U – "Утром встаешь с головной болью".

Оно может быть представлено в виде следующей логи­ческой формулы:

(X&Y)→(Z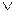U)

2. Второе составное высказывание состоит из следующих простых:

Х – "Социологические исследования показывают, что по­требитель отдает предпочтение удобству".

Y –"Социологические исследования показывают, что по­требитель отдает предпочтение многообразию выбора".

Z – "Фирме следует сделать упор на усовершенствование товара".

U – "Фирме следует сделать упор на увеличение многооб­разия новых форм".

Логическая формула второго составного высказывания:

(X&Y)→(Z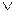U)

Пример 3. Записать формулами логики высказываний два способа доказательства равенства множеств:

1. Множества X и Y равны, если для любого элемента a из того, что а принадлежит Х, следует, что а принадлежит Y, и из того, что а не принадлежит Х, следует, что а не принадлежит Y:

2. Множества X и Y равны, если для любого элемента a из того, что а принадлежит Х, следует, что а принадлежит Y, и из того, что а принадлежит Y, следует, что а принадлежит Х.

Обозначим простые высказывания:

А – «Элемент а принадлежит Х, т.е. а Х»,

В – «Элемент а принадлежит Y, т.е. а Y»,

С – «Множества X и Y равны, т.е. X=Y».

Тогда процедура доказательства, исходя из первого определения:

«Если из А следует В, и из 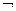А следует 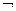В, то С» или:

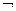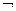((А→В)&(A→B))→C

Второе определение представимо следующей формулой:

«Если из А следует В, и из В следует А, то С» или:

((А→В)&(В→А))→C