2014-02-04
670
Порядок решения уравнения с использованием
 |
Введем в ячейку В17 формулу 3*С11^2+2*C11-15. В ячейку С17 введем начальное значение х=-1. Результат приведен на листинге 6.16 в столбцах В и С.
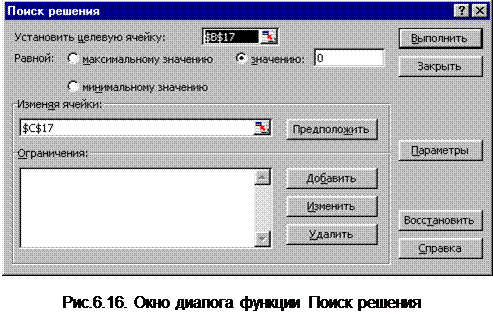
Введем команду Сервис, Поиск решения – открывается одноименное окно диалога (рис. 6.16).
Введем в строку “Установить целевую ячейку” адрес ячейки, содержащей формулу В17, установим переключатель Значение и в строку вода “значению” введем значение “0”, а в строку “Изменяя ячейки” введем адрес ячейки содержащий значение Х - С17 с абсолютным адресом. Щелкнем по кнопке Выполнить. Открывается окно “Результаты поиска решения” (рис. 6.17). Для получения результата щелкните по кнопке ОК. В ячейке В17 отобразится значение точности поиска решения, а в ячейке С17- значение корня. Для сравнимости результатов на Листинге 6.16 результаты помещены в столбцах E и F. Результат решения не зависит от выбранного начального значения корня. Сравните результаты в строках 17 и 18. Однако Функция Поиск решения, также как и функция Подбор параметра позволяет найти только один корень уравнения. Для получения значения второго корня необходимо изменить начальное значение. В строке 19 приведен результат поиска второго корня.
|
|
|
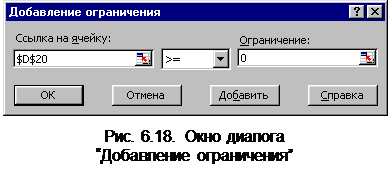Второй корень можно найти при любом начальном значении Х, если установить ограничения на его значение. Щелкните по кнопке Добавить в окне диалога Поиск решения (рис. 6.16). Открывается окно диалога “Добавление ограничения” (рис. 6.18). Выберите в списке “Ссылка на ячейку” адрес ячейки, содержащей значение х, например, D20, в среднем списке - знак отношения, а в списке “Ограничения” введите значение ограничения, например, “0” и щелкните по кнопке ОК. Результат будет записан в окне “Ограничения” окна диалога Поиск решения (рис.6.16). Пример решения приведен в строке 20 Листинга 6.16.
Из анализа результатов на Листинге 6.16. можно сделать следующие выводы: Функция Поиск решения дает более точные результаты по сравнению с функцией Подбор параметра, при этом результат не зависит от начального приближения. Функция может найти только одно решение, поэтому поиск значения корня необходимо вести на отрезке отделения.
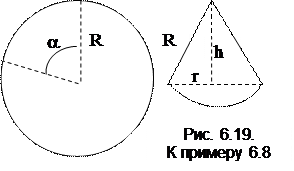Пример 6.8. Задача о “пожарном ведре”. Дана заготовка из жести в виде круга диаметром R=0,75 м. Требуется выкроить из него конусообразное ведро таким образом, чтобы объем ведра был наибольший.
Разработаем математическую модель:
Объем пожарного ведра Q=1/3hSосн, Sосн= pr2,
где r – радиус основания конуса, h – высота ведра, h=корень(R2-r2)
Радиус основания зависит от угла вырезки a. Длина окружности основания ведра l=(2p-a)R или l=2pr, отсюда
r=(2p-a)R/ (2p),
Q=1/3*Корень(R2-((2p-a)R/ (2p))^2)*p*(2p-a)R/ (2p))2 (6.21)
|
|
|
| Листинг 6.17. Оптимизация | |
| Задача о пожарном ведре | |
| Q=1/3*Корень(R2-(2p-a)R/ (2p))*p*(2p-a)R/ (2p))2 | |
| Исходные данные: | |
| R= | 0,75 |
| Угол альфа | Целевая функция |
| 1,84 | 0,046875 |
Объем ведра Q должен максимизироваться, поэтому выражение (6.21) называют целевой функцией. Оптимизируемым параметром является угол a. Ограничение в данном выражении одно: угол a должен быть больше 0, но меньше
 |
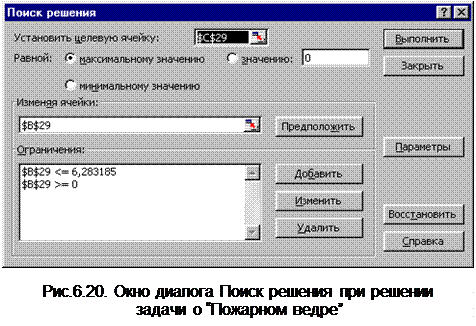2p. Решение приведено на Листинге 6.17. Окно диалога приведено на рис. 6.20.
