Понятие средней величины (СВ). Способы расчета средней.
Структурные средние.
Понятие средней величины (СВ). Способы расчета средней.
Каждая однородная статистическая совокупность состоит из массы отдельных единиц, кот. обладают индивидуальными особенностями и поэтому отличаются друг от друга по размеру кол-ного признака.
Для получения обобщающей хар-ки большого кол-тва индивид. значений варьирующего признака рассчитываются средние величины.
Следует отметить, что к средней величине обращаются не только тогда, когда речь идёт о вариации признака, но и когда необходимо дать обобщающую инф-цию по всей совокупности.
Под средней величиной понимают обобщающий показатель, хар-щий типичный уровень или размер варьирующего признака в расчете на единицу однородной совокупности в конкретных условиях места и времени.
Таким образом средняя величина – это величина, кот. одним значением хар-ет нечто общее для совокупности в целом.
Средняя величина в статистике:
1) хар-ет типичный уровень варьирующего признака;
2) отражает то общее, что хар-но для всех единиц совокупности;
3) взаимопогашает различия, кот. наблюдаются у отдельных единиц совокупности.
Средние величины могут быть исчислены по непосредственному перечню значений варьирующего признака у каждой единицы совокупности.
Т.е. средняя величина может быть рассчитана по первичным несгруппированным данным и по сгруппированным данным. Такие средние назыв. простыми и взвешенными.
Если средние вычисляются по варьирующему ряду сгруппированной инф-ции с учетом статистического веса каждого варианта, то их назыв. взвешенными средними.
Способы расчета средней зависят:
1) от того какой инф-цией мы обладаем для расчета средней;
2) от хар-ра осреднённой величины.
Исходной базой расчета и критерием правильности выбора формы средней величины явл. исходное соотношение средней или смысловая формула.
Смысловая формула – это словесное описание методологии расчета средней величины.
Общий вид смысловой формулы:

Для каждого среднего показателя используемого в соц.-экон. анализе можно составить только одну смысловую формулу для расчета среднего показателя.
Пример.
Составим смысловую формулу для расчета средней ЗП.
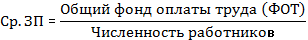
Средняя цена ед. продукции:
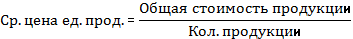
Средний стаж 1-го работника:
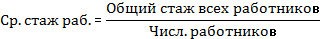
Средний процент выполнения плана по выпуску про-ции:

Выбор формы и вида средней величины происходит след. образом:
1) если известен знаменатель смысловой формулы и неизвестен числитель, то используют среднюю арифметическую;
2) если известен числитель смысловой формулы и неизвестен знаменатель, то выбираем форму средней гармонической;
3) если исходная инф-ция несгруппирована, то используют простую среднюю;
4) если исходная инф-ция сгруппирована, то используют среднюю взвешенную.
В статистике применяются 2 наиболее распространённых вида средней величины: средняя арифметическая и средняя гармоническая. При этом каждый из этих видом может иметь 2 формы: простую или взвешенную.
Средняя арифметическая простая – это отношение суммы значений признака в отдельных единицах совокупности к числу единиц совокупности.
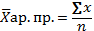
x – значение признака в каждой единицы совокупности
n – кол-тво единиц совокупности.
Средняя арифметическая взвешенная – это отношение общего размера значений признака во всех единицах сгруппированной совокупности к численности единиц во всех группах.
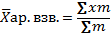
m – веса, т.е. число ед. совокупности в каждой отдельной группе или может быть удельный вес каждой отдельной группы.
Средняя гармоническая простая – это обратное значение средней из обратных значений варьирующего признака, т.е. вариантов.
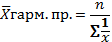
Средняя гармоническая взвешенная – это обратное значение средней из обратных значений варьирующего признака во всех единицах сгруппированной совокупности.
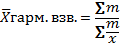
Для наглядности нарисуем схему форм и видов средних величин:
| Средние величины: | |||
| Формы: | Виды: | ||
| простая | взвешенная | суммарные: | структурные |
| - параболические; - логарифмические; - степенные (арифметическую, гармоническую, гармоническую | - мода; - медиана; - децили; - квартили |
Пример.
По пр-ю, занимающемуся торговлей ценных бумаг, имеются данные о приобретении акций в 2-х акционерных обществах.
| АО | Август | Сентябрь | ||
| Кол-тво приобр. акций, шт (m) | Цена 1 акции, грн (x) | Стоим-ть приобр. акций, грн (m) | Цена 1 акции, грн (x) | |
| №1 | ||||
| №2 | ||||
| Итого | х | х |
Опр-ть среднюю цену одной приобретённой акции по 2-м акционерным обществам в августе и сентябре.
Как изменилась средняя цена акции в абсолютном и относительном выражении.
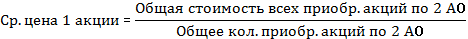
Т.к. инф-ция сгруппирована и в смысловой формуле известен знаменатель и неизвестен числитель будем использовать среднюю арифметическую взвешенную.
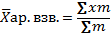
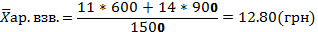
В августе по 2-м акционерным обществам акции скупали в среднем по цене 12,80 (грн) за единицу.
Т.к. в сентябре месяце в смысловой формуле известен числитель и неизвестен знаменатель, инф-ция сгруппирована, веса неравны, то будем использовать среднюю гармоническую взвешенную.
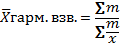
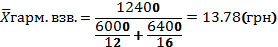
В сентябре по 2-м АО в среднем скупали по 13,78 грн за единицу.
Абсолютное значение изменения ед. акции:
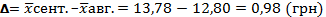
Относительное значения изменения ед. акции:

14.09.
В сентябре месяце по сравнению с августом средняя цена одной акции выросла на 0,98 грн или в 1,077 раза, т.е. на 7,7%
Модой в статистике назыв. наиболее часто встречающиеся значения признака либо варианта совокупности. В дискретном вариационном ряду мода – это вариант, обладающий наибольшей частотой.
Для опр-ния моды в интервальном вариационном ряду сначала отыскивается модальный интервал (т.е. интервал, обладающий наибольшей частотой), а в рядах с неравными интервалами – по наибольшей плотности распределения.
Формула моды для интервальных вариационных рядов с равными интервалами:
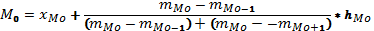
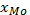 – нижняя граница модального интервала (интервала,
– нижняя граница модального интервала (интервала,
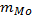 – частота модального интервала
– частота модального интервала
 – частота предмодального интервала
– частота предмодального интервала
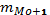 – частота постмодального интервала
– частота постмодального интервала
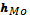 – ширина модального интервала.
– ширина модального интервала.
Медиана – это значение признака у той единицы совокупности, кот. делит упорядоченный, ранжированный вариационный ряд пополам, т.е. половина совокупности имеет значение меньше медианы, а другое – больше.
В дискретном вариационном ряду медиана – это интервал, кот. находится в центре ранжированного ряда.
Нахождение медианы в интервальном вариационном ряду требует предварительного нахождения медианного интервала.
Таким интервалом будет тот, накопленная (коммулитативная) частота кот. равна или превышает полу сумму частот ряда распределения.
После опр-ния медианного интервала, медиана вычисляется путём линейной интерпретации, т.е. по формуле:

– это нижняя граница;
– частота медианного интервала;
 – накопленная частота в предмедианном интервале или накопленная частота до медианы;
– накопленная частота в предмедианном интервале или накопленная частота до медианы;
– ширина медианного интервала.
Пример.
Имеются след. данные о распределении работников пр-я по уровню ЗП
| ЗП, грн | Числ. раб., чел. | S, чел | х’, грн (середина интервала) | x’m, грн. |
| 200-300 | ||||
| 300-400 | ||||
| (Ме) 400-500 | (mме) 4 | (Sме) 10 | ||
| 500-600 | ||||
| Итого | х | х |
Опр-ть моду и медиану.
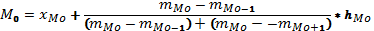
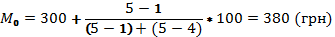
На данном пр-и чаще всего встречаются работники с ЗП 380 грн.

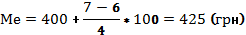
Половина работников данного пр-я получают ЗП менее 425 грн, другая половина – больше.
Расчет средней величины в интервальном вариационном ряду распределения несколько отличается от расчета в дискретном вариационном ряду.
Для опр-ния средней величины в интервальном вариационном ряду распределения необходимо сначала найти середину ряда, таким образом перейдя от интервального вариационного ряда распределения к дискретному, потом расчет средней происходит обычным способом.
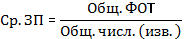
Обоснование формы и вида ср. величины.
Т.к. в смысловой формуле известен знаменатель, инф-ция сгруппирована, веса неравны, и мы осуществили переход от интервального вариационного ряда к дискретному, то будем использовать среднюю арифметическую взвешенную модифицированную.
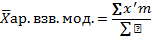
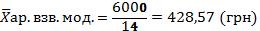
Работники данного пр-я в среднем получают 428,57 грн.
Наряду с медианной для более полной хар-ки стр-ры изучаемой совокупности применяют и др. значения вариантов, занимающих в ранжированном ряду опр-ное положение. К ним относятся квартили и децили.
Квартили делят ряд по сумме частот на 4 равные части, а децили – на 10 частей.
Расчет этих показателей в вариационном ряду аналогичен расчету медианы и начинается с нахождения порядкового номера соотв. варианта и опр-ния по накопленной частоте того интервала, в кот. этот вариант находится. Затем с помощью линейной интерпретации, т.е. по формуле.
Квартиль находится по формуле:
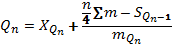
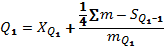
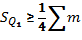
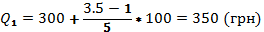
25% работников получают ЗП менее 350 грн, 75% - более.
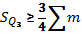
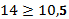
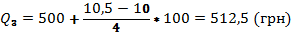
75% работников получают ЗП менее 512,5 грн, а 25% - ниже.
19.09.
Формула для децилей в интервальном вариационном ряду имеет след. вид:
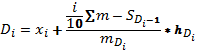
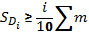
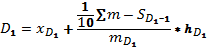
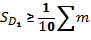
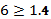
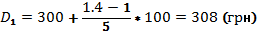
Вывод 10% получают ЗП получают менее 308 грн, а 90% - более.
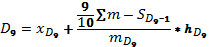
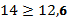
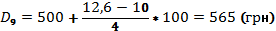
90% работников получают ЗП ниже 560 грн, 10% - свыше 560 грн.
 2014-02-04
2014-02-04 8592
8592
