Пример составления математической модели теплоэнергетической
Метод расчета сис-мы балансовых у-ний с учетом структуры.
Сходимость метода Зейделя, в связи с непосредственным использованием при расчете значения текущей итерации выше, чем у методов простого и модифицированного. Кроме того метод Зейделя позволяет использовать структурную особенность теплотехнической сис-мы. Как было показано ранее для любой реальной схемы, можно найти такую последовательную расчетную цепочку эл-ов, когда все зависимые пар-ры последующего определяются по пар-рам предыдущего. Таким образом, у-ние в сис-ме расставляется согласно последовательности цепочки эл-ов и начальное приближение необходимо задавать только пар-ры эл-ов, которые находятся в начале расчетной цепочки.
Задана схема ГТУ:

К1 – 1-ая ступень компрессора.
К2 – 2-ая ступень компрессора.
ОВ – охладитель воздуха.
Т1–1-ая камера сгорания.
Т2 – 2-ая камера сгорания.
ГТ1 – 1-ая ступень газовой турбины.
ГТ2 – 2-ая ступень газовой турбины.
ЭГ – электрогенератор.
В – воздух.
Вд – вода.
Т – топливо.
д.г. – дымовые газы.
1. Формализованное описание схемы.
Для описания схемы составим граф вида:
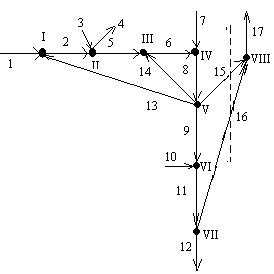
Которую опишем с помощью структурной матрицы (матрица связи).
| I | II | III | IV | V | VI | VII | VIII | 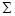
| |
| -1 | |||||||||
| -1 | -1 | ||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 | -1 | ||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 | -1 |
Входящую связь обозначаем - +1, выходящую – -1.
Матрица видов связи:
| Взд | вода | т-во | ПС | МЭ | ЭЭ | |
ПС – продукты сгорания.
МЭ – механическая энергия.
ЭЭ – электрическая энергия.
2. Дополнительно составляем матрицы: смежности, пр-сов, контуров.
Матрица смежности:
| I | II | III | IV | V | VI | VII | VIII | |
| I | ||||||||
| II | ||||||||
| III | ||||||||
| IV | ||||||||
| V | ||||||||
| VI | ||||||||
| VII | ||||||||
| VIII | ------ | ------ | ------ | ------ | ----- | ------- | ------ | ------ |
Имеется пустая VIII строка, это значит, что связь 8 не входит в контур, и ее можно рассчитать отдельно.
Матрица пр-сов: Матрица контуров:
| I | -2 | ||||
| II | -4 | -5 | |||
| III | -6 | ||||
| IV | -8 | ||||
| V | -9 | -13 | -14 | -15 | |
| VI | |||||
| VII | -12 | -16 | |||
| VIII | -17 |
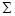
| |||||||||||
3. Сис-ма балансовых у-ний.
Составим упрощенную сис-му у-ний, состоящую только из материальных и энергетических балансов.
Сис-му сводим в таблицу:
| № эл-та | Графическое у-ние | Балансовое у-ние | примечание |
| I | 
|
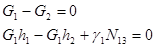
|
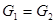 (1)
(1)
|
| II | 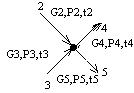
| 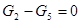
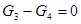
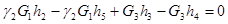
| 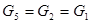
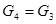 (2)
(2)
|
| III | 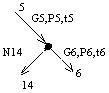
|
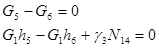
|
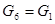 (3)
(3)
|
| IV | 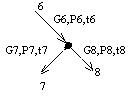
|
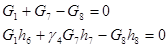
| (4) (5) |
| V | 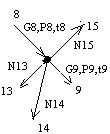
|
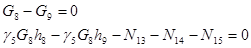
|
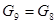 (6)
(6)
|
| VI | 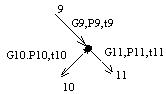
|
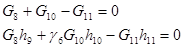
| (7) (8) |
| VII | 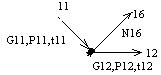
| 
| 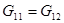 (9)
(9)
|
| VIII | 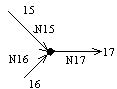
|
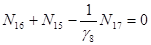
| (10) |
Параллельно в записи у-ний рекомендуется составлять таблицу переменных, в следующей форме:
| № эл-та | наименование | единицы измерения | обозначения | идентификатор | диапазон измерений | примечание |
4. сис-ма ограничения.
В данном разделе указываются диапазоны измерения основных переменных, и тем самым определяется область исследования.
5. ф-ции качества.
В качестве критерия эффективности принимаем КПД установки, и в этом случае ф-ция качества будет представлена у-нием:
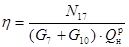 .
.
6. анализ переменных мат. модели и выбор зависимых и независимых пар-ров.
Расходы:
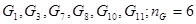 .
.
Энтальпия:
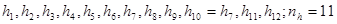 .
.
Мощности:
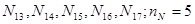 .
.
Коэф. потерь:
У нас 8 эл-ов, поэтому будет 8 значений потерь.
Общее число переменных: 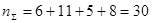 .
.
Степень свободы: 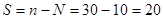 .
.
В 1-ую очередь задаются конструктивные пар-ры, к которым в данном случае можно отнести коэф. потерь, далее задаются теплофизические пар-ры (т-ра и давление) по которым находим энтальпию. Часто приходиться для этого вводить дополнительное у-ние.
В частности, в данном случае, т-ра на выходе из компрессора или газовой турбины м.б. однозначно определена, если заданная т-ра на входе и соответственно степень сжатия или расширения. Из группы расходов и мощностей задается минимальное число переменных, обычно это или расход т-ва или мощ-ть.
В данном случае мы можем определить электрическую мощ-ть установки, и тогда расходы т-ва будут зависимыми, или можем произвести расчет в предельных единицах, задав расход воздуха равного единице. В рез-те получим удельную электрическую мощ-ть и удельные расходы т-ва отнесенный на единичный расход т-ва.
В табличных переменных в примечании указывается, какие переменные явл-ся зависимыми, какие нет, какие регламентированные какие нет.
Если G1 = 1 кг/с, то остается 10 у-ний, все энтальпии необходимо задавать.
Для определения, из какого у-ния находим, неизвестный пар-р, находит сокращенную матрицу функциональных связей, где строки считаются по числу у-ний, столбцы – по неизвестным пар-рам.
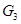
| 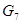
| 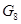
| 
| 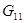
| 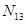
| 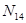
| 
| 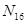
| 
| 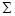
| |
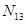
| |||||||||||
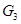
| |||||||||||
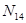
| |||||||||||
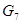
| |||||||||||
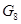
| |||||||||||

| |||||||||||

| |||||||||||
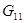
| |||||||||||
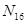
| |||||||||||

| |||||||||||
1-ца в i-j эл-те матрицы означает, что j-ая переменная входит в i-ое у-ние. Присматриваем все столбцы, в которых только одна единица. Далее просматриваем строки, и ищем, где есть только одна 1-ца.
Если в строке находится только одна 1-ца, то данное у-ние м.б. рассчитано отдельно от всей сис-мы.
Алгоритм повторяется, но уже по 2 переменным (по двум единицам).
 2014-02-04
2014-02-04 523
523








