СНС с настраиваемой моделью

Теперь рассмотрим СНС с настраиваемой моделью. В этом случае на модель, как и на систему управления, подаётся пробный сигнал либо синусоидальный (при стабилизации АЧХ), либо импульсный (например, с генератора белого шума).

Остановимся на СНС со стабилизацией АЧХ, применяемой при относительно медленном изменении свойств ОУ по сравнению со временем перерегулирования. В такой СНС на каждый переменный параметр ОУ выделяется своя частота.

Пусть количество переменных параметров ОУ равно 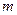. Для подстройки модели (М) на вход системы (рис. 10.3), кроме основного медленно меняющегося сигнала 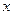, подаётся пробный сигнал 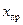(наиболее часто синусоида), содержащий весь спектр частот. Изменение каждого параметра модели (амплитуды каждой частоты) под воздействием пробного сигнала сравнивают с изменением параметров системы управления. На основании результатов сравнения изменяют параметры УУ.

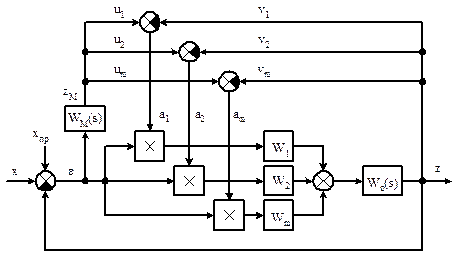Рисунок 10.3 – Схема СНС со стабилизацией АЧХ

Система будет стабилизирована, если для каждой частоты 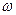разница между выходными сигналами модели 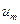и системы управления 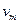равна нулю, т.е. 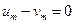. Это условие выполняется, если передаточные функции модели 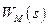и системы управления совпадают. Математически это можно записать следующим образом:

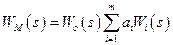. (10.12)

Условие (10.2) должно выполняться только для резонансных (соответствующих переменным параметрам ОУ) частот 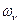, т.е.

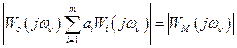, . (10.13)

Для выделения сигнала резонансной частоты 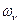используются узкополосные фильтры 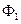, …, 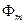. Из выражения (10.13) видно, что

. (10.14)

Для выбора только положительных значений коэффициентов 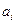используются детекторы (диоды). Для поддержания 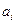неизменимыми при отсутствии рассогласования между моделью 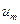и проектируемой системой 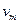ставятся интеграторы.

С учётом этого полную схему СНС можно изобразить следующим образом (рис. 10.4).

Как видно из схемы рис. 10.4

.

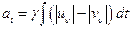Найдём 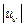и 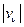. Согласно рис. 10.4

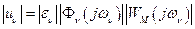, ; (10.15)

. (10.16)

Тогда

. (10.17)

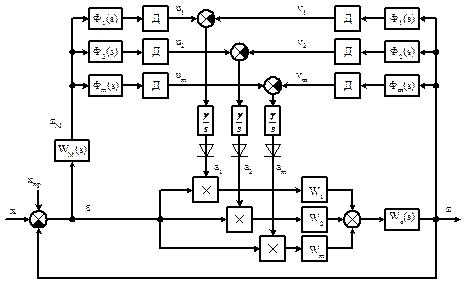Рисунок 10.4 – Функциональная схема СНС со стабилизацией АЧХ:

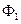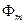, …, - фильтры, настроенные на частоту, соответствующую изменяющимся параметрам ОУ;

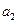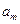, , …, - варьируемые параметры УУ (умножители);

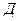– детекторы (выпрямители), которые выделяют постоянную составляющую;

- интегрирующая цепочка

Поскольку 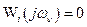при 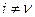, то получаем 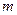независимых уравнений первого порядка для 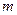переменных параметров ОУ:

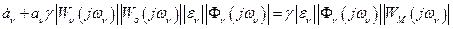. (10.18)

Таким образом, полученное уравнение (10.18) для СНС со стабилизацией АЧХ описывает изменение варьируемых параметров 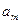в зависимости от сигнала рассогласования .

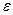При импульсном (быстром) изменении свойств ОУ используются СНС со стабилизацией импульсной характеристики.

Как и в случае CНC со стабилизацией АЧХ, при стабилизации импульсной характеристики на вход модели и на вход проектируемой системы подаётся импульсный сигнал. На выходах модели и проектируемой системы их сигналы сопоставляются, в результате чего изменяются параметры УУ до тех пор, пока не будет достигнуто соответствие между реальной импульсной характеристикой проектируемой системы и характеристикой модели.

В качестве пробного импульсного сигнала наиболее часто используется сигнал в форме белого шума (случайный процесс).

Связь между входным 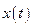и выходным 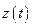сигналами при импульсном воздействии (белом шуме) описывается с помощью корреляционной функции:

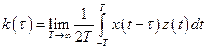. (10.19)

Чтобы практически измерять функцию 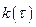при значениях 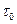, , 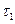…, 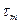её аргумента, необходимо на эти величины задержать процесс 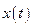относительно 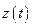, а затем провести интегрирование (10.19), но с пределами от 0 до и отнормировать делением на . Наиболее часто для задержки 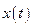относительно 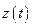используют линии задержки, реализующие функцию 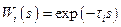. Учитывая это, схему СНС со стабилизацией импульсной характеристики можно изобразить в виде, представленном на рис. 10.5.

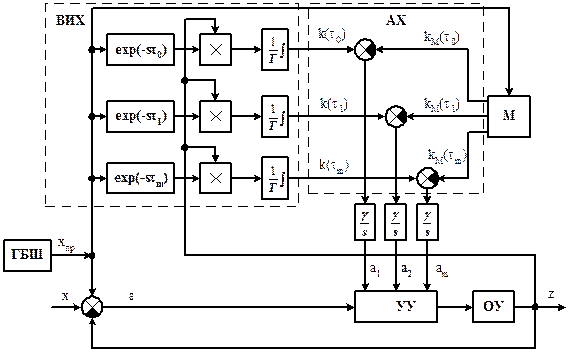Рисунок 10.5 - Схема СНС со стабилизацией импульсной характеристики:

ВИХ – вычислитель импульсной характеристики;

АХ – анализатор характеристик;

ГБШ – генератор белого шума.

Описание схемы: на вход проектируемой системы и вычислителя импульсной характеристики ВИХ подаётся пробный сигнал из генератора белого шума (ГБШ). В ВИХ осуществляется многоканальная задержка пробного сигнала на величину 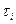, перемножение 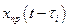с выходным процессом системы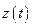и интегрирование соответствующих произведений с целью вычисления дискретных значений 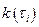импульсной характеристики замкнутой системы .

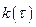В анализаторе характеристик АХ эти значения 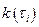сравниваются с аналогичными значениями импульсной характеристики модели 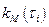. Результаты сопоставления интегрируется устройствами , выходы которых являются варьируемыми параметрами УУ. Изменение параметров УУ будет происходить до тех пор, пока выходные сигналы АХ не обратятся в нули, т.е. пока реальная импульсная характеристика не совпадет с импульсной характеристикой модели.

Необходимо отметить, что в модели также присутствует аналогичный ВИХ (на схеме не показана). Кроме того, в АХ не обязательно должны сопоставляться импульсные характеристики системы и модели. В АХ может вычисляться некоторый критерий качества, зависящий от и сопоставляться с эталонным значением.