СНС с эталонной моделью

Вопросы для самопроверки

1. Какие системы называются адаптивными? Какие их особенности? Что называется однократной и многократной адаптациями?

2. Как классифицируются адаптивные системы? Чем они отличаются?

3. Какие существуют подходы и схемы адаптивных систем?

ТЕМА 10 АНАЛИТИЧЕСКИЕ СНС СО СТАБИЛИЗАЦИЕЙ КАЧЕСТВА УПРАВЛЕНИЯ

Применение модели в СНС позволяет упростить структуру СНС.

В зависимости от назначения модели СНС делятся на два больших класса:

- СНС с эталонной моделью;

- СНС с настраиваемой моделью.

Если влияние внешней среды на характеристики объекта известны и параметры УУ изменяются по предварительно полученным законам, то применяются СНС с эталонной моделью. В этом случае модель представляет собой заданный эталон желаемых свойств реальной системы, который не меняется, если диапазон изменения параметров воздействия не значителен. В противном случае эталонная модель перестраивается и для определённого диапазона изменения параметров остаётся неизменной. При использовании эталонной модели друг с другом сравнивают не параметры и характеристики контура ОУ+УУ, а выходные сигналы основного контура системы и модели.

Во втором случае модель вначале определяет реальные характеристики системы, то есть идентифицирует систему управления, и сравнивает с известными параметрами модели желаемой разомкнутой системы, подстраиваясь под характеристики реальной системы, а затем стабилизирует или оптимизирует свойства реальной системы, если они изменяются в процессе последующего функционирования системы.

Схема СНС с моделью–эталоном, отражающей желаемые свойства замкнутой системы управления, изображена на рис. 10.1.

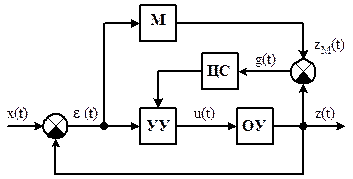Рисунок 10.1 – Схема СНС с эталонной моделью:

М – модель;

ЦС – цепь самонастройки

Принцип работы СНС с эталонной моделью: сигнал рассогласования 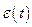подаётся на вход модели М и на вход цепочки УУ+ОУ. На выходе ОУ сигнал 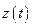сравнивается с выходным сигналом модели 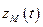. При их не совпадении вырабатывается сигнал отклонения 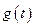, который, воздействуя на цепь самонастройки (ЦС), изменяет параметры УУ до тех пор, пока выходные сигналы модели 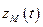и объекта управления 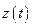совпадут.

Наиболее важным этапом синтеза СНС с эталонной моделью является разработка алгоритма ЦС, чтобы сигнал отклонения 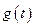был ограниченным и со временем стремился к нулю, что является признаком устойчивости СНС.

Наиболее универсальным для оценки устойчивости СНС является прямой метод Ляпунова: если система управления описывается совокупностью уравнений в отклонениях в форме Коши 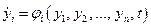, 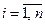и можно подобрать такую знакоопределённую функцию Ляпунова 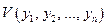, полная производная во времени 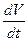от которой в некоторой области 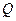является знакопостоянной функцией противоположного знака функции 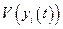, то функции 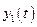, ,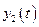..., , 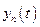будут ограниченными, а система асимптотически устойчивой.

Рассмотрим применение прямого метода Ляпунова для синтеза СНС второго порядка.

Пусть в разомкнутом состоянии (без модели) реальная система управления описывается уравнением

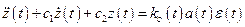, (10.1)

где 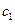и 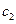-неизменяемые параметры ОУ;

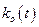- изменяющийся во времени коэффициент усиления ОУ;

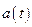- коэффициент усиление управляющего устройства, который является варьируемым параметром УУ.

Пусть уравнение модели имеет аналогичный вид:

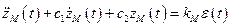. (10.2)

Необходимо найти такой процесс изменения коэффициентов 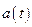, который приведёт к устранению рассогласования 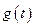между выходными сигналами ОУ 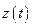и модели 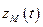и обеспечит асимптотическую устойчивость. Синтезируем такую СНС.

Так как 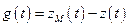, то вычтем из (10.2) (10.1). Получим

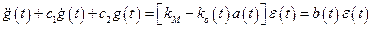, (10.3)

где .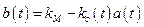

Запишем (10.3) в форме Коши, обозначив ; .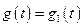

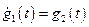Тогда уравнение (10.3) можно переписать в виде:

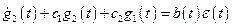или

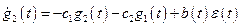. (10.4)

Введём функцию Ляпунова 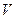в форме квадратичной положительно определённой функции переменных 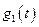,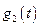и коэффициента :

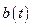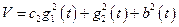. (10.5)

Найдём полную производную по времени 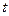от функции :

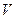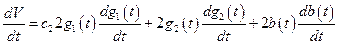. (10.6)

С учётом (10.4) выражение (10.6) можно записать:

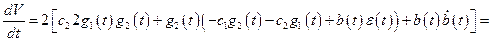
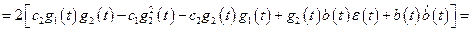
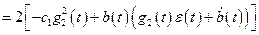. (10.7)

Чтобы производная 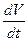была отрицательно определённой, необходимо, чтобы 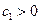, а 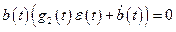при любых 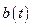и .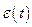

Отсюда следует, что

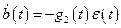. (10.8)

При медленно изменяющемся 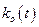(система настраивается быстрее, чем изменяются свойства ОУ) можно записать, что

, (10.9)

где 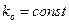- известное номинальное значение коэффициента усиления ОУ;

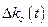- медленно изменяющаяся составляющая.

Подставив в (10.8) выражения 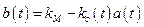и (10.9), получим:

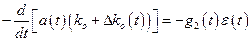. (10.10)

Так как 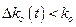, то вторым слагаемым в левой части (10.10) можно пренебречь. Тогда 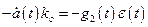или .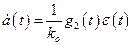

Откуда следует, что варьируемый параметр УУ

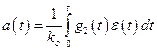. (10.11)

Изобразим структурную схему СНС второго порядка с моделью (рис. 10.2).

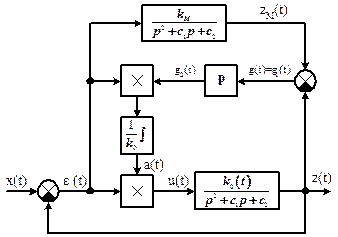Рисунок 10.2 – Структурная схема СНС второго порядка с моделью