2014-02-04
1305
В градиентных методах необходимо определять градиент функции 
. Если конкретный вид функции известен, то эти вычисления осуществляются аналитически и затем результаты используются в структуре алгоритмов поиска экстремумов. Однако во многих задачах функция в явном виде не известна, но можно измерять её значения. В этих случаях для нахождения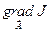 
используется либо метод численного дифференцирования, либо метод синхронного детектирования.
Метод численного дифференцирования используется для определения градиента 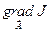, если аналитическое выражение для не задано.
Пусть известно значение функции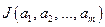 
в некоторой точке, а аналитическое выражение для неизвестно. Придадим переменой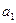 
приращение 
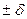и измеряем значения в точках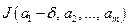 
и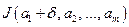 
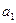. Для нахождения частной производной от функции по аргументу вычтем из 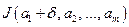значение 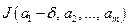и поделим на 
:
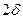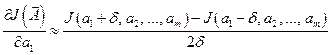. (12.18)
Затем осуществляют аналогичные измерения и вычисления для остальных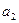 
, 
, …, 
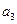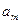и находят компоненты 
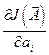для всех 
.
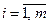Метод синхронного детектирования также используется для определения градиента 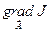, если аналитическое выражение для неизвестно.
Пусть имеется функция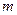 
переменных 
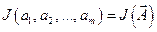. Придадим приращение каждому её аргументу 
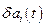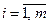, . В результате получим функцию 
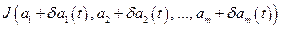. Обозначим через 
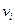произведение этой функции на приращение аргумента :
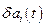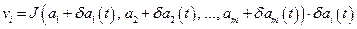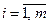, . (12.19)
Разложим функцию 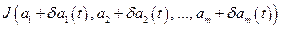в ряд Тейлора:
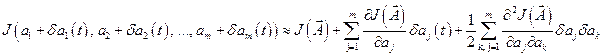. (12.20)
Подставим разложение в ряд Тейлора (12.20) в выражение (12.19).
Получим:
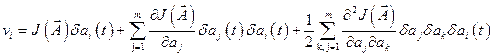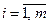, (12.21)
Найдем среднее значение величины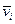 
. С этой целью процесс 
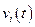можно подать на устройство, выполняющее операцию усреднения, например, фильтр 
.
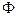, (12.22)
где 
- время усреднения.
После подстановки (12.21) в (12.22) получим
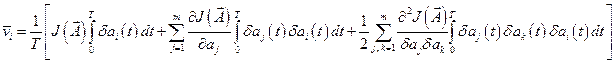. (12.23)
В качестве поисковых сигналов 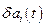обычно выбирают синусоидальных (гармонический) сигнал вида
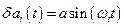(12.24)
с частотой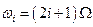 
, где 
.
Определим первое слагаемое в (12.23), подставив в него (12.24):
,
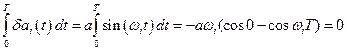где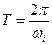 
.
Второе слагаемое* в (12.23)
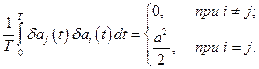(12.25)
*Доказательство (12.25) приведено в приложении А
Третье слагаемое в (12.23)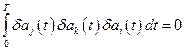 
(из-за громоздкости вычислений доказательство не приводится).
В результате получаем, что при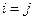 
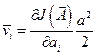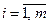, (12.26)
 |
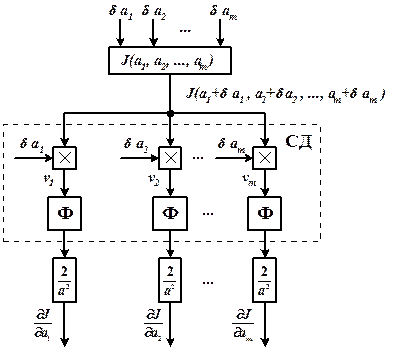Из выражения (12.26) видно, что компоненты градиента
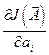будут пропорциональны среднему значению :
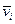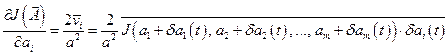. (12.27)
Устройство, умножающее 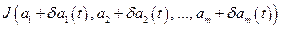на 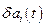и усредняющее их произведение, называется синхронным детектором (СД).
Схема определения градиента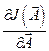 
методом синхронного детектирования представлена на рис. 12.2.
Рисунок 12.2 – Схема определения градиента методом синхронного детектирования
