Градиентные методы поиска экстремума

ТЕМА 12 ПРИНЦИПЫ ПРОЕКТИРОВАНИЯ ПОИСКОВЫХ СНС С ОПТИМИЗАЦИЕЙ КАЧЕСТВА УПРАВЛЕНИЯ

В поисковых СНС для оптимизации критерия качества используются специальные поисковые сигналы, что позволяет определить направление изменения контролируемых параметров, соответствующее приближению к экстремуму критерия качества. Основными операциями, восполняемыми поисковыми СНС с оптимизацией качества управления, являются определение градиента критерия качества и движения к экстремуму в соответствии с градиентом.

Из математики следует, что для определения оптимального (экстремального) управления необходимо найти частную производную от критерия оптимальности по его переменным и приравнять к нулю.

Пусть критерий оптимальности является функцией 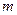переменных , , 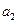…, 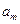вектора 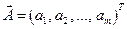. Более лаконично можно записать, что .

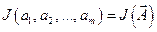Тогда условие экстремума примет вид:

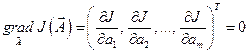. (12.1)

Методы поиска экстремума, основанные на определении градиента функции , называются градиентными.

Поиск экстремума градиентными методами включает в себя два этапа:

1) определение градиента;

2) движение к экстремуму в соответствии с информацией о градиенте.

Рассмотрим вначале методы движения к экстремуму в предположении, что градиент вычислен при любом .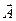

Общая форма организации движения к экстремуму градиентными методами сводится к такому изменению вектора 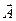, при котором скорость изменения параметров вектора 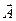связана с градиентом функции соотношением:

, (12.2)

где 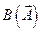- некоторая квадратичная 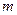-матрица, зависящая от параметров вектора .

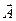В зависимости от вида матрицы 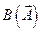существует несколько алгоритмов движения к экстремуму.

Алгоритм 1 - метод градиента.

В настоящее время это один из наиболее распространённых методов градиентного поиска экстремума. Он применяется, если скорость изменения вектора 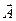пропорциональна градиенту от критерия качества:

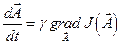, (12.3)

где 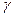- некоторый постоянный коэффициент. Причём при поиске максимума 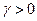, при поиске минимума .

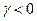В развернутом виде алгоритм (12.3) примет вид:

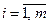, . (12.4)

При сравнении (12.4) с (12.2) видно, что 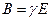, где 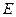- единичная матрица.

Сущность метода градиента: по заданным параметрам вектора 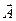находится градиент 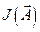. Потом каждый компонент вектора 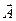изменяется со скоростью, пропорциональной составляющей градиента по этому компоненту, и снова определяется градиент 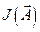. Операции повторяются, пока не выполнится условие (12.1).

Схематически метод градиента можно изобразить в виде рис.12.1:

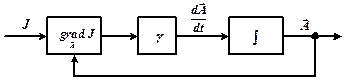Рисунок 12.1 – Схема реализации метода градиента

При машинных способах поиска экстремума, метод градиента реализуется в дискретной форме. В этом случае параметры вектора 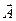изменяются скачкообразно:

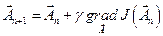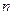, =0, 1, 2, … (12.5)

или в развёрнутом виде

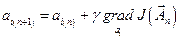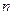, =0, 1, 2, …, 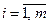(12.6)

Сущность алгоритма сводится к следующему: задаются некоторое начальное значение 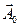вектора 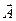; в этой точке вычисляют градиент 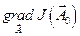и каждая составляющая вектора 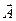получает приращение, пропорциональное частной производной функции по этой составляющей в точке 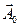. По формуле (12.5) получают следующую точку 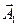. Далее те же действия выполняют в точке 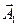, получая точку 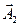и т.д.

Вычисления по принципу (12.5) продолжаются до тех пор, пока при некотором значении 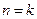не будут выполнены условия при поиске максимума или минимума соответственно

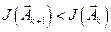; (12.7)

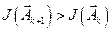. (12.8)

При выполнении условий (12.7) или (12.8) поиск останавливают и оптимальному значению вектора 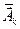присваивается значение .

Коэффициент 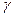влияет на шаг алгоритма: при малых значениях 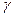увеличивается количество расчётов, при больших значениях 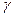алгоритм может оказаться расходящимся. Поэтому на практике чаще используется переменный коэффициент 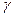, принимающий на каждом шаге свое значение .

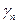Алгоритм II – метод наискорейшего спуска.

Этот алгоритм отличается от метода градиента только тем, что вектор 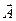изменяется с постоянной скоростью, пропорциональной только градиенту в заданной начальной точке 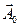, а не в каждой точке 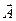, как в методе градиента:

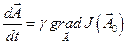(12.9)

или в скалярной форме

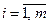, , (12.10)

где .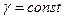

В отличие от метода градиента в методе наискорейшего спуска градиент вычисляется лишь в начальной точке 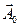, а дальнейшее движение происходит в направлении, обусловленном начальным значением градиента 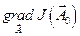. Изменение вектора 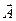по правилу (12.9) происходит до тех пор, пока не будет получено условие

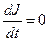. (12.11)

Если условие (12.11) выполняется в точке 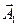, то этим значением 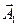заменяют начальную точку 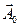в (12.9) и процесс поиска повторяется, пока не будет получено условие (12.1):

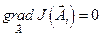. (12.12)

Хотя метод наискорейшего спуска является многоцикловым, (вначале ищется точка 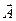, в которых выполняется условие (12.11), а потом условие (12.12)), но в пределах одного цикла градиент вычисляется только один раз – вначале цикла.

В дискретной форме движение в пределах цикла осуществляется пошагово:

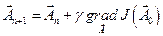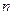, =0, 1, 2, … (12.13)

Аналогично методу градиента цикл поиска 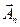продолжается до тех пор, пока не выполнится одно из условий (12.7) или (12.8). При достижении условий (12.7) или (12.8) точке 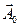присваивается значение и цикл повторяется, но при другом значении аргумента функции 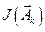, т.е.

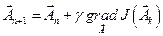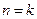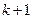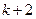, , , , … (12.14)

Здесь видно, что в каждом цикле шаг будет свой, пропорциональный .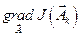

Операцию повторяют, пока модуль разности значений функции в начальной и конечной точках очередного цикла не будет меньше установленной малой величины. В результате получаем экстремальное значение вектора .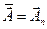

Алгоритм III – обобщённый метод Ньютона.

Во многих практических задачах наиболее быстро можно достичь экстремума в (12.2), если в качестве матрицы 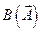использовать отрицательную обратную матрицу вторых производных от функции по :

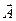. (12.15)

В этом случае алгоритм движения к экстремуму называется обобщённым методом Ньютона, а матрица вторых производных (12.15) - матрицей Гессе или гессианом.

Тогда алгоритм движения к экстремуму (12.2) приобретёт вид:

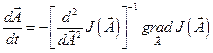(12.16)

или в дискретной форме

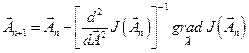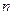, =0, 1, 2, … (12.17)

Сущность обобщенного метода Ньютона аналогична методу градиента, но при условии, что 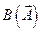не является .

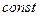Алгоритм IV - метод Гаусса-Зайделя.

Сложностью I-III алгоритмов является то, что экстремум ищется при одновременно изменяющихся аргументах функции .

В методе Гаусса-Зайделя вначале определяется экстремальные значения функции , изменяя только аргумент 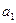, используя метод градиента, т.е. формулы (12.4) и (12.6) примут вид:

;

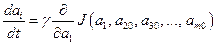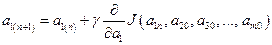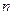, =0, 1, 2, …

После определения экстремального значения аргумента 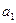функции , для которой выполняются условия (12.1) (при непрерывном поиске) или (12.7), (12.8) (при шаговом поиске), по такой же методике, определяется экстремальное значение аргумента 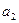при постоянных 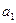, ,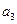..., . 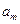Затем изменяют аргумент 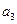и т.д. последовательно до переменной 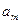. После этого весь цикл поиска повторяют, снова начиная с 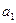, и так до тех пор, пока не будут выполняться условия (12.1) или (12.7), (12.8).