Рис. 4.8 Рис. 4.9
Рис. 2.30
Рис. 2.29
Рис. 2.28
Синхронными реактивными называют микродвигатели с переменным вдоль окружности воздушного зазора магнитным сопротивлением и невозбужденным ротором. Вращающееся магнитное поле таких микродвигателей создается только м.д.с. статора. Изменение магнитного сопротивления вдоль окружности воздушного зазора двигателя осуществляют путем выбора соответствующей формы и материала ротора.
РЕАКТИВНЫЕ МИКРОДВИГАТЕЛИ
ЛЕКЦИЯ №12
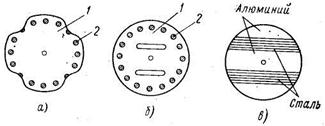
Роторы, схематически изображенные на рис. 2.28, а, б (здесь 1 – сердечник из электротехнической стали; 2 – стержни короткозамкнутой обмотки), отличаются от обычного короткозамкнутого ротора типа «беличья клетка» асинхронного микродвигателя только наличием внешних открытых (явнополюсная конструкция, рис. 2.28, а) или внутренних (неявнополюсная конструкция, рис. 2.28, б) пазов, которые обеспечивают изменение магнитного сопротивления вдоль окружности. У ротора, показанного на рис. 2.28, в, такой же эффект получают за счет выполнения его из двух разнородных по магнитным свойствам материалов.
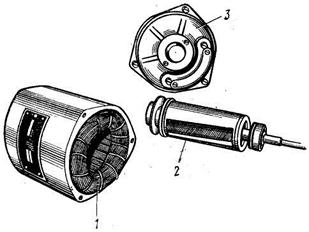
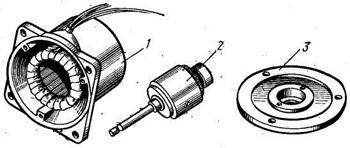
На рис. 2.29 представлен синхронный реактивный микродвигатель типа СД с ротором, показанным на рис. 2.28, а. На рис. 2.29 обозначено: 1 – статор с двухфазной обмоткой; 2 – ротор; 3 – подшипниковый щит.
Принцип действия реактивного микродвигателя рассмотрим на статической модели, представленной на рис. 2.30. Вращающееся магнитное поле статора Φ1 заменим постоянным магнитом, магнитная ось которого совпадает с направлением м.д.с. статора. Угол между осью м.д.с. статора и продольной осью d ротора обозначим γ.
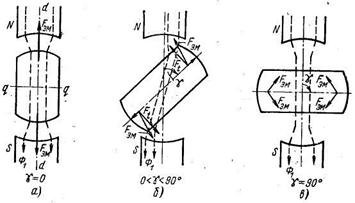
На рис. 2.30, а показано положение ротора в случае, когда угол между осями ротора и потока статора γ = 0. Магнитные силовые линии проходят по пути наименьшего сопротивления и не деформируются. Реактивный вращающий момент Mp = 0. Ротор занимает положение устойчивого равновесия. Если принудительно повернуть ротор на угол γ по часовой стрелке (рис. 2.30, б), то магнитные силовые линии изогнутся.
Деформация магнитного поля вследствие упругих свойств силовых линий вызовет реактивный вращающий момент, стремящийся повернуть ротор против часовой стрелки. Очевидно, ротор установится под таким углом к оси потока статора, при котором внешний момент уравновесится реактивным моментом двигателя. При устранении внешнего момента ротор снова вернется в положение устойчивого равновесия, при котором γ = 0. При повороте ротора на 90° (рис. 2.30, в) силовые линии поля будут вновь проходить прямолинейно, не изгибаясь, но магнитное сопротивление в этом случае будет больше, чем при γ = 0.
Реактивный момент Mp = 0, т.е. ротор находится в равновесии. Однако между положениями равновесия при γ = 0 и γ = 90° имеется существенное различие. В первом случае равновесие устойчиво, так как при всяком отклонении от него ротор стремится вернуться в первоначальное положение. Во втором случае равновесие неустойчиво и достаточно малейшего возмущения, чтобы ротор вернулся в устойчивое положение максимальной магнитной проводимости, показанное на рис. 2.30, а или отличающееся от него на 180°.
Таким образом, реактивный момент всегда стремится установить ротор в положение минимального магнитного сопротивления на пути потока двигателя. Положение устойчивого равновесия ротора будет при γэ = 0 или 180° и неустойчивого – при γэ = 90 или 270°.
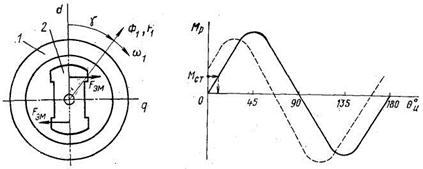
Нами был рассмотрен физический процесс создания реактивного вращающего момента в статическом режиме при смещении оси ротора относительно оси полюсов постоянного магнита. В реальных синхронных реактивных микродвигателях обмотки статора 1 создают вращающееся магнитное поле, а ротор 2 увлекается реактивным моментом вслед за полем и вращается с угловой скоростью поля (рис. 2.31).
Аналитические выражения реактивного момента через угол γ весьма громоздки. Поэтому при расчетах используют угол θu между результирующим вектором напряжения статора и поперечной осью q ротора, значение которого тоже зависит от момента нагрузки.
Вид угловой характеристики реактивного двигателя определяется законом изменения магнитного сопротивления вдоль окружности статора. Момент, соответствующий основной (второй) гармонике переменной составляющей магнитного сопротивления, без учета активного сопротивления обмотки статора находят по формуле, известной из общей теории явнополюсных электрических машин:
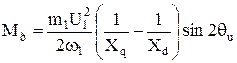 , (2.35)
, (2.35)
Реактивный вращающий момент Мр в отличие от активного изменяется в функции угла θu по закону sin 2θu (сплошная линия на рис. 2.32). Установившийся режим в микродвигателе наступает при определенном угле θu, обеспечивающем равенство Мр = Мст, где Мст – статический момент сопротивления на валу двигателя.
У реальных синхронных микродвигателей активное сопротивление обмотки статора R1 относительно велико и соизмеримо с Xd и Xq. Поэтому для расчета реактивного момента нужно пользоваться уточненными формулами (2.32) и (2.33):
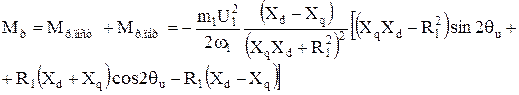 (2.36)
(2.36)
При R1 = 0 выражение (2.36) обращается в (2.35). Из формулы (2.36) следует, что сопротивление R1 влияет на значение момента Mр. Максимум момента смещается с 45° в сторону меньших углов θu = 30÷40° (пунктирная линия на рис. 2.32).
Пересчет угловой характеристики Mp = f(θu) в зависимости Mр = f(γ) производят по формуле
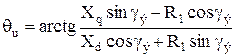 ,
,
где γэ = pγ.
Угловые характеристики Mр = f(γэ) несинусоидальны, но при углах γэ = 0, 90, 180 и 270° момент Mр = 0.
При неравенстве угловых скоростей ротора и поля угол θu становится периодической функцией времени и среднее значение реактивного момента равно нулю. Поэтому у синхронных реактивных микродвигателей применяют асинхронный метод пуска. В качестве пусковой обмотки служит либо обмотка типа «беличья клетка» (см. рис. 2.28, а, б), либо алюминиевые части ротора (см. рис. 2.28, в). В двигателях с ротором, изображенным на рис. 2.28, б, сохранение полного комплекта стержней обмотки приводит к улучшению пусковых свойств, в частности к повышению момента входа в синхронизм.
У реактивных микродвигателей в процессе пуска вследствие изменения магнитного сопротивления RM появляется переменная составляющая магнитного потока, наводящая добавочную э.д.с. в обмотке статора. У них, как и у двигателей с постоянными магнитами, создается тормозной момент Mт, наиболее сильно искажающий характеристику результирующего момента пускового режима при угловых скоростях ротора, близких к 0,5ω1. При правильном выборе соотношения RMd и RMq влияние момента Μт на пусковые свойства реактивного микродвигателя обычно значительно слабее, так как ротор не возбужден. В синхронном режиме Мт = Мр.пост.
 2014-02-02
2014-02-02 2227
2227
