Условие задачи

Пример решения задачи целочисленного программирования.

Целочисленного программирования.

Алгоритм графического метода решения задачи

Графический метод решения задач целочисленного программирования.

При наличии в задаче линейного программирования двух переменных, а в системе ограничения – неравенств, она может быть решена графическим методом без требований целочисленных переменных.

Если оптимальное решение этой задачи является целочисленным, то оно и является оптимальным для исходной задачи.

Если же полученное оптимальное решение не целочисленное, то строится дополнительное линейное ограничение. Оно обладает следующими свойствами:

1.Оно должно быть линейным;

2.Должно отсекать найденный оптимальный не целочисленный план;

3.Не должно отсекать ни одного целочисленного плана.

1.Построить систему координат x₁0х₂ и выбрать масштаб.

2.Найти область допустимых решений (ОДР) системы ограничений задачи.

3.Построить целевую функцию, являющуюся линией уровня и на ней указать направление нормали.

4.Переместить линию целевой функции по направлению нормали через ОДР, чтобы она из секущей стала касательной к ОДР и проходила через наиболее удаленную от начала координат точку. Эта точка будет являться точкой экстремума, т.е. решением задачи.

Если окажется, что линия целевой функции параллельна одной из сторон ОДР, то в этом случае экстремум достигается во всех точках соответствующей стороны, а задача линейного программирования будет иметь бесчисленное множество решений.

5.Найти координаты, точки экстремума и значение целевой функции в ней. Если полученные значения не целочисленные, то перейти к следующему шагу.

6.Выделить у этих координат область с целочисленными значениями.

7.Определить новые координаты и построить граф.

8.Найти точки с целыми значениями искомых переменных, подставить в уравнение целевой функции и найти её значение. Максимальное из полученных значений целевой функции и будет решением задачи.

Решить методом ветвей и границ задачу, имеющую следующую математическую модель.

Решение:

1.Находим координаты точек каждого линейного уравнения системы ограничений и строим прямые

1 прямая: 3х₁+2х₂=1

-если х₁=1, то 2х₂=12, х₂=6

-если х₂= 0, то 3х₁=12, х₁=4

2 прямая: 2х₁+5х₂=20

-если х₁=0, то 5х₂=20, х₂=4;

-если х₂=0, то 2х₁=20, х₁=10

2.Находим ОДР.

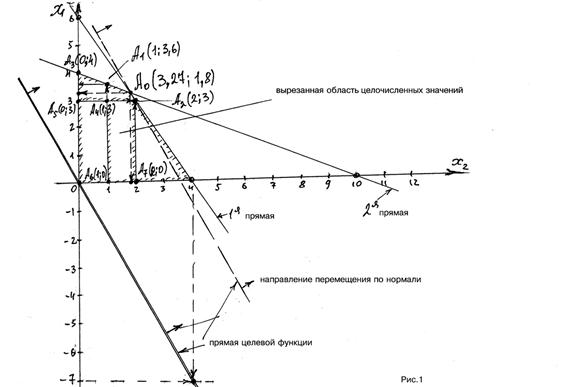
Так как х₁, х₂ ≥ 0, то область будет ограничен прямыми ОХ₁ и ОХ₂ и построенными прямыми (см. рис.1).

3.Находим координаты точек целевой функции и строим прямую целевой функции:

7х1+4х2=0

- первая точка х₁=0; х₂=0

- вторая точка х₁=4, х₂=(-7).

4.Перемещаем прямую целевой функции по направлению через ОДР до тех пор, пока она не станет касательной к ней, и находим точку А₀.

5.Находим координаты точек А₀ и значение целевой функции в ней:

Х1=1,8; х2=3,27;

Z=7×1,8+4×3,27=12,6+13,08=25,68

Получен не целочисленный оптимальный план

6.выделим область относительно точки А₀ беря целые значения 1 ≤ х₁ ≤ 2; 3 ≤ х₂ ≤ 4.

Получим координаты точек по границе этой области:

А₁ (1;3,6) А₂ (2;3); А₃ (0;4); А₄ (1;3); А₅ (0;3); А₆ (1;0); А₇ (2;0).

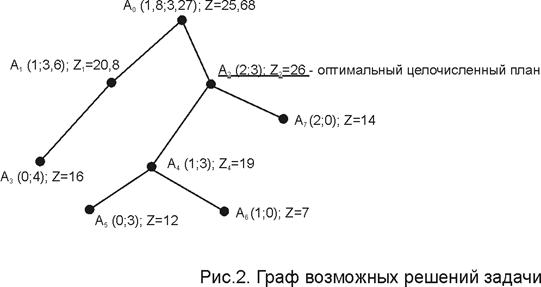
7.Строим граф (рис.2)

8.Для точек с целыми значениямиих координат (искомые значения х₁ и х₂) находим значения целевой функции:

Для точки А₂ (2;3) Z₂= 7×2+4×3=26

Для точки А₃ (0;4) Z₃= 7×0+4×4=16

Для точки А₄ (1;3) Z₄= 7×1+4×3=19

Для точки А₅ (0;3) Z₅= 7×0+4×3=12

Для точки А₆ (1;0) Z₆= 7×1+4×0=7

Для точки А₇ (2;0) Z₇= 7×2+4×0=14

Так как максимальное значение целевой функции находится для точки А2 (2;3), то она и будет оптимальным целочисленным решением задачи.

Ответ: Z=26; х₁=2; х₂=3.

5.4. Задача о коммивояжере.

Имеется необходимость посетить n городов в ходе деловой поездки. Спланировать поездку нужно так, чтобы, переезжая из города в город, побывать в каждом не более одного раза и вернуться в исходный город. Определить оптимальный маршрут посещения городов и его минимальное расстояние.

Задана матрица расстояний между городами c_ij.

Сформулированная задача - задача целочисленная. Пусть х_ij = 1, если путешественник переезжает из i -ого города в j-ый и х_ij = 0, если это не так.

Формально введем (n+1) город, расположенный там же, где и первый город, т.е. расстояния от (n+1) города до любого другого, отличного от первого, равны расстояниям от первого города. При этом, если из первого города можно лишь выйти, то в (n+1) город можно лишь придти.

Введем дополнительные целые переменные, равные номеру посещения этого города на пути. u₁ = 0, u_n+1 = n. Для того, чтобы избежать замкнутых путей, выйти из первого города и вернуться в (n+1) введем дополнительные ограничения, связывающие переменные x_ij и переменные u_i. (u_i целые неотрицательные числа).

2. Математическая модель

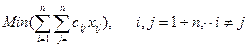
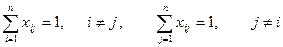
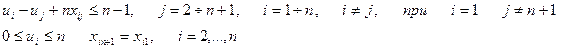
5.5.Пример решения задачи.

Условия задачи:

Необходимо посетить 4 города в ходе деловой поездки Спланировать поездку нужно так, чтобы, переезжая из города в город, побывать в каждом не более одного раза и вернуться в исходный город. Определить оптимальный маршрут посещения городов и его минимальное расстояние.

Матрица расстояний c_ij между городами задана таблицей:

Номер города

Решение задачи.

Составляем математическую модель задачи.

Z_min=19х₁₂+25х₁₃₊11х₁₃₊37х₂₁+26х₂₃+58х₂₄+10х₃₁+50х₃₂+39х₃₄+38х₄₁+39х₄₂+24х₄₃

х₁₂+х₁₃+х₁₄=1 х₂₁+х₃₁+х₄₁=1

х₂₁+х₂₃+х₂₄=1 х₁₂+х₃₂+х₄₂=1

х₄₁+х₄₂+х₃₄=1 х₁₃+х₂₃+х₄₃=1

х₂₁+х₂₃+х₂₄=1 х₁₄+х₄₂+х₃₄=1

U₁ - U₂ + 4х₁₂ < 3

U₁ –U₃ + 4х₁₃ < 3

U₁ – U₄+ 4х₁₄ < 3

U₂ – U₃ + 4х₂₃ < 3

U₂ –U₄ + 4х₂₄ < 3

U₃ – U₂+ 4х₃₂ < 3

U₃ – U₄ + 4х₃₄ < 3

U₄ – U₂ + 4х₄₂ < 3

U₄ –U₃ + 4х₄₃ < 3

U₄ – U₁+ 4х₄₁ < 3

U₃ – U₁ + 4х₃₁ < 3

U₂ –U₁ + 4х₂₁ < 3

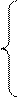
0,

Х_ij= - ЦЕЛЫЕ,

где:

Z_min - минимальный маршрут посещения городов;

c_ij - расстояние между городами ij;

U_i - номер посещения i – го города.

Строим граф посещения городов с учетом возможных маршрутов движения коммивояжера.

Граф посещения городов:

2

4

4

4

3

19

25 11

58 50 39 24 39

39 24 58 39 50 26

38 10 38 37 37 10

122 111 171 140 122 86

где:

--- расстояние между городами;

--- расстояние, пройденное по маршруту;

--- расстояние, пройденное по минимальному маршруту.

Номер города

Ответ:

Минимальный маршрут: 1 --- 4 --- 2 --- 3 --- 1.

Минимальное расстояние – 86 ед.