Постановка задачи. 1.Сформулируйте постановку задачи целочисленного программирования

Контрольные вопросы.

1.Сформулируйте постановку задачи целочисленного программирования.

2.Математическая модель задачи целочисленного программирования, ее особенности.

3.Метод ветвей и границ и его применение.

4.Алгоритм графического решения задачи целочисленного программирования.

5.Как построить граф целочисленной области возможных решений задачи?

6.Как определить целочисленный план и экстремальное значение целевой функции?

7.Сформулируйте задачу о коммивояжере.

8.Какие экономико-математические модели могут быть сведены к задаче о коммивояжере?

9.Как построить математическую модель задачи о коммивояжере?

10.Как называются переменные в математической модели задачи о коммивояжере?

6.Лекция. Динамическое программирование.

Динамическое программирование – раздел оптимального программирования (оптимального управления), в котором процесс принятия решения и управления, может быть разбит на отдельные этапы (шаги).

Динамическое программирование позволяет свести одну сложную задачу со многими переменными ко многим задачам с малым числом переменных. Это значительно сокращает объем вычислений и ускоряет процесс принятия управленческого решения.

Экономический процесс является управляемым, если можно влиять на ход его развития.

Управление – совокупность решений, принимаемых на каждом этапе для влияния на ход развития процесса.

Операция – управляемый процесс, т.е. мы можем выбирать какие-то параметры, влияющие на ход процесса и управлять шагами операции, обеспечивать выигрыши на каждом шаге и в целом за операцию.

Решение на каждом шаге называется «шаговым управлением».

Совокупность всех шаговых управлений представляет собой управление операцией в целом.

При распределении средств между предприятиями шагами целесообразно считать номер очередного предприятия; при распределении на несколько лет ресурсов деятельности предприятия – временной период. В других задачах разделение на шаги вводится искусственно.

Требуется найти такое управление (х), при котором выигрыш обращался бы в максимум:

F(x)=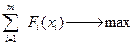

Где F – выигрыш за операцию;

F_i(x_i) – выигрыш на i-м шаге;

х – управление операцией в целом;

х_i – управление на i-м шаге (i=1,2,…,m). В общем случае шаговые управления (х₁, х₂, … х_m) могут стать числами, векторами, функциями.

То управление (х*), при котором достигается максимум, называется оптимальным управлением. Оптимальность управления состоит из совокупности оптимальных шаговых управлений х* = х*₁, х*₂, … х*_m

F* = max {F*(х*)} – максимальный выигрыш, который достигается при оптимальном управлении х*.

Исходя из условий, каждой конкретной задачи длину шага выбирают таким образом, чтобы на каждом шаге получить простую задачу оптимизации и обеспечить требуемую точность вычислений.