2014-02-04
638
Основным методом динамического программирования является метод рекуррентных соотношений; который основывается на использовании принципа оптимальности, разработанного американским математиком Р.Беллманом.
Суть принципа:
Каковы бы ни были начальное состояние на любом шаге и управление, выбранное на этом шаге, последующие управления должны выбираться ОПТИМАЛЬНЫМИ относительно состояния, к которому придет система в конце каждого шага.
Использование данного принципа гарантирует, что управление, выбранное на любом шаге, не локально лучше, а лучше с точки зрения процесса в целом.
Условная оптимизация
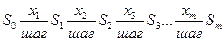
Безусловная оптимизация
Si – состояние системы на i-м шаге. Основная рекуррентная формула динамического программирования в случае решения задачи максимизации имеет вид:
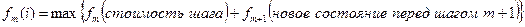, где максимум в данной формуле берется по всем возможным решениям в ситуации, когда система на шаге m находится в состоянии i.
Величина fm(i) – есть максимальная прибыль завершения задачи из состояния i, если предположить, что на шаге m, система находится в состоянии i.
|
|
|
Максимальная прибыль может быть получена максимизацией суммы прибылей самого шага m и максимальной прибыли шага (m+1) и далее, чтобы дойти до конца задачи.
Планируя многошаговую операцию надо выбирать управление на каждом шаге с учетом всех его будущих последствий на ещё предстоящих шагах.
Управление на i-м шаге выбирается не так, чтобы выигрыш именно на данном шаге был максимальным, а так, чтобы была максимальна сумма выигрышей на всех оставшихся шагах плюс данный шаг.
Среди всех шагов последний шаг планируется без оглядки на будущее, т.е. чтобы он сам, как таковой принес наибольшую выгоду.
Задача динамического программирования начинает решаться с конца, т.е. с последнего шага. Решается задача в 2 этапа:
1 этап (от конца к началу по шагам): Проводится условная оптимизация, в результате чего находится условные оптимальные управления и условные оптимальные выигрыши по всем шагам процесса.
2 этап (от начала к концу по шагам): Выбираются (прочитываются) уже готовые рекомендации от 1-го шага до последнего и находится безусловное оптимальное управление х*, равный х*1, х*2, …, х*m.
