2014-02-04
1074
Пусть дано дифференциальное уравнение:
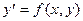
с начальными условиями:
.
Решение в каждой точке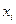 
определяется по формуле:
,
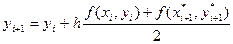где
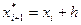
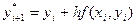
Геометрически это означает, что определяется направление интегральной кривой в исходной точке 
и во вспомогательной точке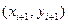 
, а в качестве окончательного направления ломаной берется среднее этих направлений.
Пример.
Пусть дано дифференциальное уравнение:
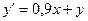
с начальными условиями:
.
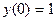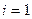
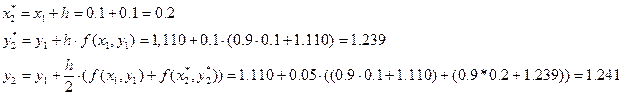Решение ОДУ имеет вид:
 |  |
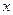| 0.0 | 1.000 |
| 0.1 | 1.110 |
| 0.2 | 1.241 |
