Методы решения ОДУ

Задача Коши.

Задача Коши, или задача с начальными условиями, имеет следующие дополнительные условия:

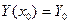
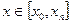
Краевая задача.

Когда дополнительные условия заданы как в точке 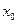, так и в точке .

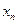Задача на собственные значения.

Если функция 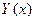зависит от параметров :

,

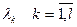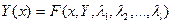где .

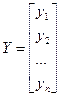
Число дополнительных условий должно быть соответственно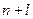. Функции 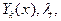где 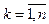; 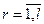удовлетворяющее всем уравнениям, называются собственными дифференциальными или собственными значениями задачи.

Обыкновенные дифференциальные уравнения могут быть решены следующими методами:

1. аналитическими;
2. численными;
3. графическими;
4. приближенными.

Аналитические методы дают решение в виде аналитического выражения.

Графические методы дают приближенное решение в виде графика.

Численные методы дают частное решение для определенных 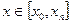в виде таблицы, Численные методы применяются только к корректно поставленным задачам, т.е. к таким, у которых малое изменение начальных значений, приводит к малому изменению интегральных кривых.

Пример.

Пусть дано следующее ОДУ:

.

Необходимо решить задачу Коши для .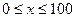

Начальные условия имеют вид:

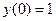
Общее решение имеет вид:

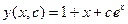
при 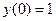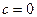решение .

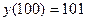Однако при малом изменении начальных условий:

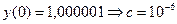решение в точке 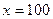: 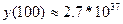. То есть имеет место плохо обусловленная задача.