1. Определяем активные, реактивные и полные проводимости ветвей по формулам:
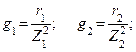
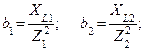
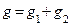
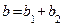
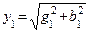
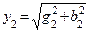
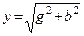
2. Определяем токи в ветвях: 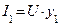

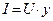
3. Определяем мощности ветвей и всей цепи:
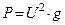
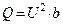
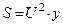 .
.
Параллельное соединение активно-индуктивного и
активно-емкостного сопротивления
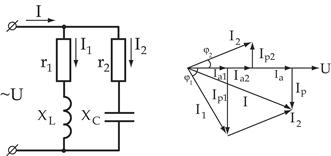
| |
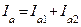
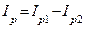
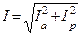
| 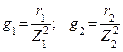
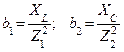
|
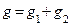
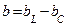
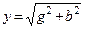
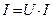
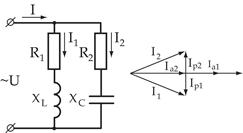
Общий случай неразветвленной цепи
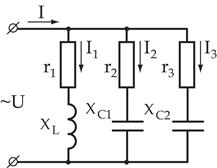
| 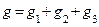
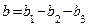
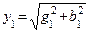
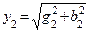
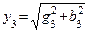
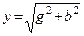
|
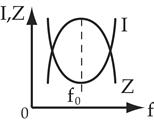
Резонанс токов
В цепи резонанс токов наступает, если 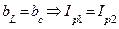 .
.
| 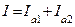 - чисто активный характер, т.к. реактивные точки - чисто активный характер, т.к. реактивные точки 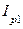 и и 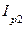 компенсируют друг друга компенсируют друг друга
|
Реактивная проводимость всей цепи 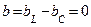
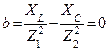
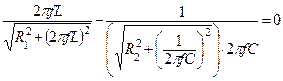
Решая это уравнение относительно частоты, получим выражение для резонансной частоты:
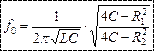
| Если 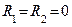 или
или 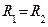 , то , то
| 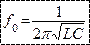

|
При резонансе полная проводимость цепи 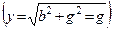 будет минимальной, а полное сопротивление – максимальным. Следовательно, ток будет минимальным.
будет минимальной, а полное сопротивление – максимальным. Следовательно, ток будет минимальным.
| Реактивные мощности ветвей 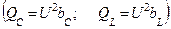 равны, поэтому реактивная мощность всей цепи равна нулю. Это означает, что обмена энергией между цепью и источником нет. Источник обеспечивает цепь только активной энергией. равны, поэтому реактивная мощность всей цепи равна нулю. Это означает, что обмена энергией между цепью и источником нет. Источник обеспечивает цепь только активной энергией.
|
 2014-02-04
2014-02-04 596
596








