Простейший генератор переменного тока представляет собой магнитную систему, состоящую из двух полюсов, причем, форма полюсов такова, что магнитная индукция в воздушном зазоре распределяется по синусоидальному закону, т.е. значение магнитной индукции в любой точке 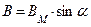 .
.
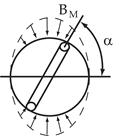
Допустим, за время t рамка развернулась на угол a, тогда угловая скорость 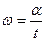 .
.
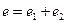
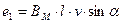
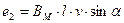
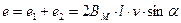
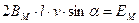
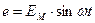
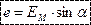
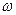 - угловая скорость (частота)
- угловая скорость (частота)
За один оборот рамка развернется на угол 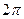 , а время оборота – период (Т), тогда угловая частота
, а время оборота – период (Т), тогда угловая частота 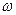 определяется:
определяется:
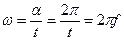
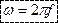
Многополюсные генераторы
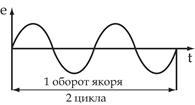
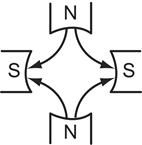 | Для получения промышленной частоты 50Гц якорь двухполюсного генератора должен вращаться со скоростью 50 об/с или 3000 об/мин. Если скорость вращения меньше, то необходимо увеличить число пар полюсов. У многополюсных генераторов за 1 оборот якоря ЭДС совершает Р циклов своих |
изменений, где Р – число пар полюсов. Если число оборотов в минуту n, то число циклов в минуту будет 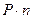 , а в секунду
, а в секунду 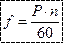
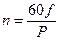
Действующее и среднее значения переменного тока
Действующее значение переменного тока численно равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, выделяет за время, равное 1 периоду, одинаковое количество тепла. Все приборы показывают действующее значение 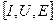 .
.
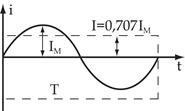 | 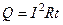 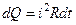 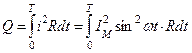 |
Если левые части уравнения равны, то и правые будут тоже равны. Приравняв правые части и выполнив операцию интегрирования, получим:
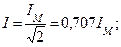
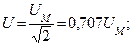
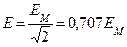
Среднее арифметическое значение переменного тока определяется в течении полупериода; если через поперечное сечение проводника в течении 1 полупериода будет протекать один и тот же заряд при постоянном и переменном токе, то такое значение постоянного тока будет равно среднему значению переменного тока 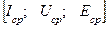 .
.
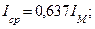
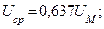
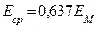
Среднее значение тока за период равно нулю.
Коэффициенты формы и амплитуды
Отношение действующего значения переменного тока (напряжения или ЭДС) к среднему значению называется коэффициентом формы 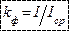 , а отношение амплитудного значения к действующему – коэффициентом амплитуды
, а отношение амплитудного значения к действующему – коэффициентом амплитуды 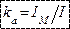 .
.
Для синусоидального тока:
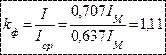 , а
, а 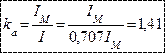 .
.
Для кривых, имеющих более острую форму, чем синусоида: 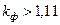 ;
; 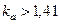 .
.
Начальная фаза. Сдвиг фаз
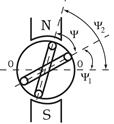 | Предположим, что в магнитном поле генератора находится два одинаковых витка, сдвинутых в пространстве друг относительно друга на угол 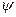 . При вращении в них буду находится ЭДС одинаковой частоты и амплитуды. . При вращении в них буду находится ЭДС одинаковой частоты и амплитуды. |
Но т.к. витки сдвинуты в пространстве, то наводимая в них ЭДС будет достигать амплитудных и нулевых значений не одновременно.
В начальный момент времени 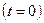 ЭДС витка будет:
ЭДС витка будет:
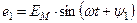
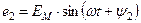
В этих выражениях углы 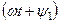 и
и 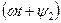 называются фазными, или фазой. Углы
называются фазными, или фазой. Углы 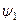 и
и 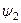 называются начальной фазой. Фазный угол определяет значение ЭДС в любой момент времени, а начальная фаза определяет значение ЭДС в начальный момент времени.
называются начальной фазой. Фазный угол определяет значение ЭДС в любой момент времени, а начальная фаза определяет значение ЭДС в начальный момент времени.
Разность начальных фаз двух синусоидальных величин одинаковой частоты и амплитуды называется углом сдвига фаз
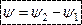
Разделив угол сдвига фаз на угловую частоту, получим время, прошедшее с начала периода:
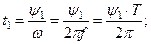
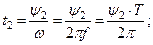
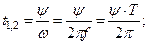
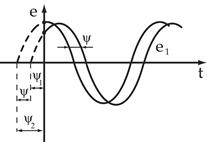 | Если угол сдвига фаз составляет 1800, то такие ЭДС находятся в противофазе |
Графическое изображение синусоидальных величин
Синусоидальные величины можно изображать графически при помощи синусоид или вращающихся векторов.
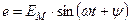
Любая синусоидальная величина характеризуется:
1. амплитудой;
2. угловой частотой;
3. начальной фазой.
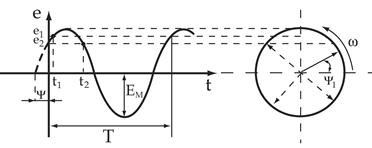
При изображении величины с помощью синусоиды ординаты синусоиды в масштабе представляют собой мгновенное значение, абсциссы – промежутки времени.
При этом длина вектора равна амплитудному значению величины, угол 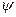 между положительным направлением оси абсцисс и векторов даст начальную фазу. Вектор вращается против часовой стрелки с угловой скоростью
между положительным направлением оси абсцисс и векторов даст начальную фазу. Вектор вращается против часовой стрелки с угловой скоростью 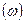 . Проекция конца вектора на ось ординат даст мгновенное значение синусоидальной величины.
. Проекция конца вектора на ось ординат даст мгновенное значение синусоидальной величины.
Совокупность нескольких синусоид называется синусоидальной (волновой) диаграммой.
Совокупность нескольких векторов называется векторной диаграммой.
Сложение и вычитание синусоидальных величин
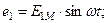
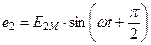 .
.
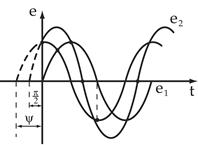
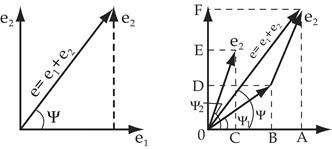
Для сложения двух синусоидальных величин с помощью синусоид необходимо сложить их ординаты в каждый момент времени.
Для того, чтобы сложить две величины с помощью векторов, необходимо к концу первого вектора добавить второй, не изменяя его величины и направления. Соединив начало первого вектора с концом второго, получим суммарный вектор.
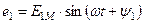
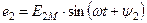
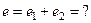
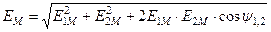
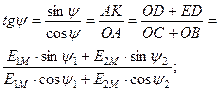
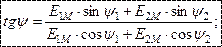
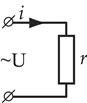
Цепи переменного тока с активным сопротивлением
 |  |
На величину тока и его характер в цепях переменного тока оказывает влияние не только сопротивление, определяемое материалом и геометрическими размерами, но и наличием в цепи емкости и индуктивности. Любая электрическая цепь обладает сопротивлением, индуктивностью и емкостью. Однако, часто тот или иной элемент преобладает над другим, поэтому их влиянием можно пренебречь.
Один и тот же проводник имеет различное сопротивление в цепях постоянного и переменного тока, причем, в цепях переменного тока это сопротивление больше.
 | - постоянный ток |
 | - переменный ток |
Это объясняется тем, что переменный ток в отличие от постоянного, который протекает по сечению проводника с равномерной плотностью, частично вытесняется из внутренних слоев проводника к наружным. В результате чего плотность тока в различных слоях неодинакова. Это явление называется поверхностным эффектом. Это объясняется тем, что внутренние слои проводника сцеплены с большим числом магнитных силовых линий, чем наружные, и поэтому в них наводится большая ЭДС самоиндукции, которая препятствует протеканию тока и вытесняет его к наружным слоям, где ЭДС самоиндукции меньше.
 | 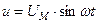 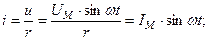 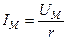 . . |
Разделив обе части равенства на 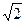 , получим действующие значения
, получим действующие значения 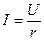 .
.
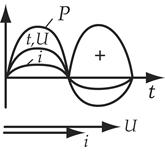
Ток и напряжение в цепи с активным сопротивлением совпадают по фазе.
 | 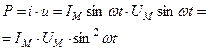 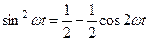 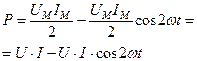 |
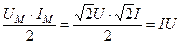
Таким образом, мощность состоит из постоянной составляющей 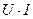 и переменной составляющей
и переменной составляющей 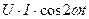 , среднее значение которых за период равно нулю. Таким образом, постоянная составляющая мощности
, среднее значение которых за период равно нулю. Таким образом, постоянная составляющая мощности 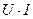 выражает среднее за период значение мощности и называется активной мощностью:
выражает среднее за период значение мощности и называется активной мощностью:
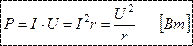
Мощность в оба полупериода положительна. Это означает, что цепь с сопротивлением r только потребляет энергию из сети и назад ее не возвращает, т.к. она преобразуется в другие виды энергии.
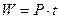
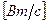
Цепи переменного тока с индуктивностью
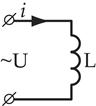 | Допустим, что под действием напряжения в этой цепи протекает ток. Под действием переменного тока в катушке возникает переменный магнитный поток, который наводи в ней ЭДС самоиндукции. 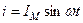 |
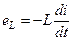
ЭДС самоиндукции 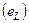 в любой момент времени уравновешивается напряжением:
в любой момент времени уравновешивается напряжением:
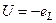
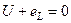
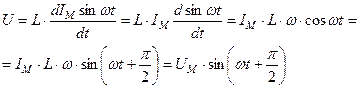
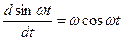
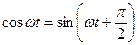
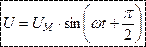
Т.о. в цепи с индуктивностью напряжение опережает ток на угол 900.
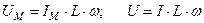
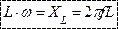
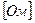 - индуктивное (реактивное) сопротивление.
- индуктивное (реактивное) сопротивление.
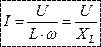 - закон Ома для цепи с индуктивностью.
- закон Ома для цепи с индуктивностью.
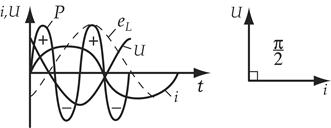
Физически индуктивное сопротивление характеризует препятствие, оказываемое переменному току в результате наличия ЭДС самоиндукции.
Мощность цепи:
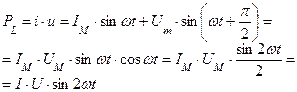
Т.о. мощность изменяется с двойной частотой и может быть положительной и отрицательной. Когда она «+» индуктивность потребляет электрическую энергию от источника и запасает ее от магнитного поля. Когда мощность «-» индуктивность возвращает запасенную энергию обратно к источнику.
Т.о. между источником и индуктивностью происходит непрерывный обмен энергией, при котором:
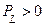 - цепь работает потребителем
- цепь работает потребителем
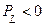 - цепь работает генератором.
- цепь работает генератором.
Максимальное значение мощности цепи индуктивности называется реактивной мощностью:
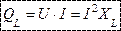
Энергия, запасенная в магнитном поле катушки, равна
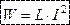
Цепь переменного тока с емкостью
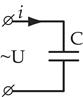 | 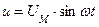 Под действием этого напряжения конденсатор будет разряжаться и заряжаться. Мгновенное значение заряда на обкладках конденсатора: Под действием этого напряжения конденсатор будет разряжаться и заряжаться. Мгновенное значение заряда на обкладках конденсатора: 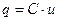 |
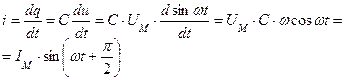
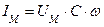
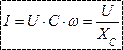 - закон Ома для цепи с емкостью.
- закон Ома для цепи с емкостью.
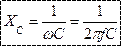 - реактивное емкостное сопротивление
- реактивное емкостное сопротивление
Т.о. ток в цепи с емкостью опережает напряжение на угол 900.
Физически емкостное сопротивление характеризует препятствие, оказываемое переменному току цепью с емкостью. В результате поляризации диэлектрика конденсатора в нем образуется свое внутренне электрическое поле, которое направлено противоположно внешнему полю, приложенному к диэлектрику.
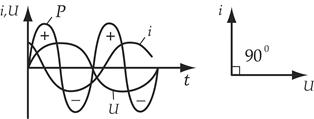
Мощность цепи:
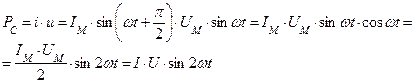
Мощность изменяется с двойной частотой относительно тока и напряжения. В течении первой четверти периода, когда напряжение, приложенное к конденсатору, возрастает, мгновенная мощность положительна. Это означает, что конденсатор получает и запасает энергию источника в виде электрического поля.
В течении второй четверти, когда напряжение, приложенное к конденсатору, уменьшается, запасенная энергия возвращается к источнику, т.е.
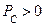 - цепь работает потребителем;
- цепь работает потребителем;
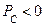 - цепь работает источником.
- цепь работает источником.
Максимальное значение мощности цепи с емкостью называют реактивной емкостной мощностью:
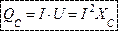
Она характеризует скорость обмена энергией между источником и цепью с емкостью.
Максимальное значение энергии, запасенной в цепи:
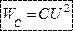
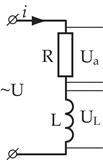
Неразветвленная цепь переменного тока с активным сопротивлением и индуктивностью
Таким сопротивлением (активным и индуктивным) обладают катушки индуктивности, обмотки трансформаторов и электрических машин.
 | 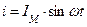 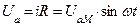 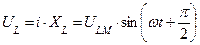 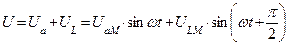 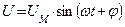 |
Т.о. напряжение опережает ток в этой цепи на угол 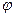 , причем
, причем 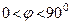 .
.
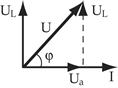 | 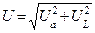 |
Мощность цепи:
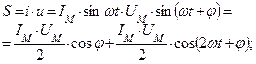
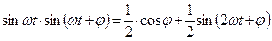
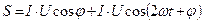
Т.о. мгновенная мощность состоит из двух составляющих: постоянной 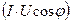 и переменной
и переменной 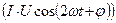 , среднее значение за период которой равно нулю.
, среднее значение за период которой равно нулю.
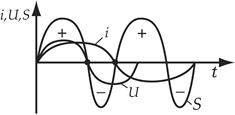
Мощность принимает как положительные так и отрицательный значения. Когда мощность положительна, то цепь потребляет энергию, а когда мощность отрицательна, то цепь возвращает запасенную энергию в цепь. Но т.к. потребляет энергию и активное сопротивление и индуктивное, а возвращает в цепь только индуктивность, то положительная будет значительно больше.
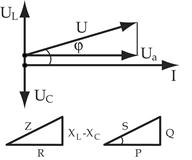
Треугольники напряжений, сопротивлений, мощностей
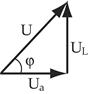 | 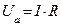 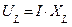 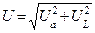 | Если стороны треугольника напряжений уменьшить или разделить на величину тока, то получим треугольник сопро-тивлений |
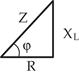 | 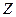 - полное сопротивление цепи - полное сопротивление цепи 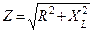 |
 | - закон Ома для цепи с активным и индуктивным сопротивлением. |
Если стороны треугольника напряжений уменьшить на ток, то получим треугольник мощностей.
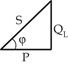 | 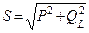 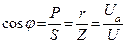 - коэффициент мощности - коэффициент мощности |
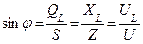
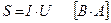
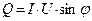 - активная мощность
- активная мощность
Коэффициент мощности показывает, какая часть полной мощности потребляется безвозвратно.
Цепь переменного тока с активным сопротивлением, емкостью и индуктивностью
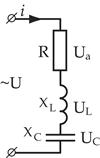 | 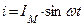 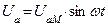 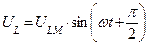 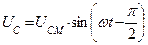 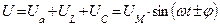 |
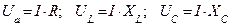
Допустим:
1. 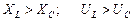
 | 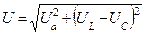 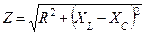 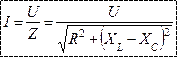 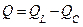 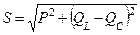 |
2. 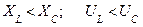
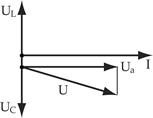 | 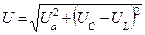 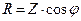 |
Общий случай неразветвленной цепи
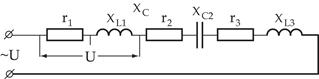
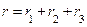
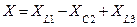
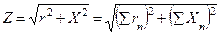
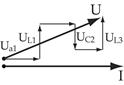
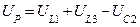
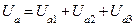
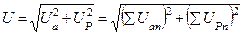
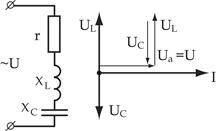 | 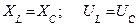 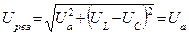 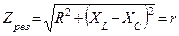 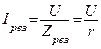 |
Результирующий ток 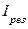 резко увеличивается, т.к. индуктивное и емкостное сопротивления компенсируют друг друга.
резко увеличивается, т.к. индуктивное и емкостное сопротивления компенсируют друг друга.
Если параметры цепи подобрать так, что 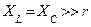 , то напряжения на емкости и индуктивности будут превышать напряжение на зажимах цепи в
, то напряжения на емкости и индуктивности будут превышать напряжение на зажимах цепи в 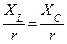 раз. Отношение
раз. Отношение 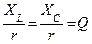 называется добротностью цепи (контура).
называется добротностью цепи (контура).
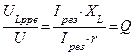
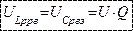
Т.о. напряжение на емкости и индуктивности будут превышать напряжение сети в 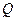 раз, что может привести к пробою диэлектрика в конденсаторе или сопротивлений изоляции индуктивности, поэтому явление резонанса напряжений в электрических цепях нежелательно, но в то же время в радиотехнике его используют (колебательные контуры приемника и передатчика).
раз, что может привести к пробою диэлектрика в конденсаторе или сопротивлений изоляции индуктивности, поэтому явление резонанса напряжений в электрических цепях нежелательно, но в то же время в радиотехнике его используют (колебательные контуры приемника и передатчика).
Возникновение напряжений на L и С, превышающих напряжение на зажимах цепи объясняется способностью емкости и индуктивности накапливать электрическую энергию.

Между емкостью и индуктивностью происходит непрерывный обмен энергией, который называется собственными колебаниями.
Частоту собственных колебаний можно определить при условии, что 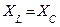 .
.
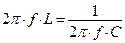 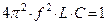 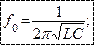 | Т.о. резонанс можно получить, изменяя частоту тока питающей сети, или изменяя емкость или индуктивность. 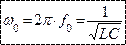 |
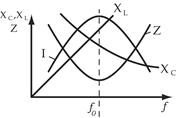
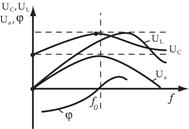
Резонансные кривые
Зависимость параметров цепи от частоты характеризуется резонансными кривыми.
 |  |
Разветвленные цепи переменного тока
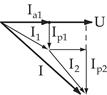
Рассмотрим цепь с двумя параллельно соединенными катушками.
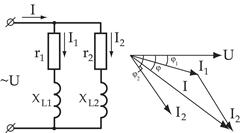 | 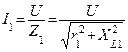 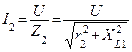 |
Для определения тока неразветвленной части цепи необходимо разложить токи 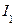 и
и 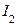 на активные и реактивные составляющие.
на активные и реактивные составляющие.
 | 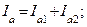 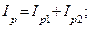 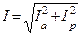 |
 2014-02-04
2014-02-04 4612
4612

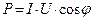 -
-