Рассмотрим систему в которой есть сила трения пропорциональная скорости. На которую действует 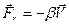
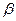 -коэффициент трения
-коэффициент трения
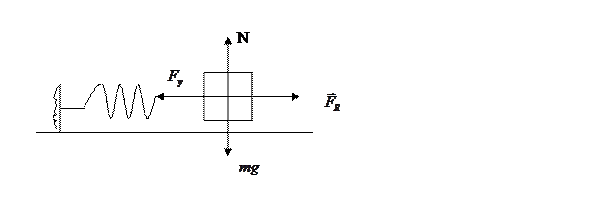
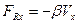
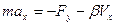
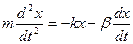
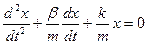
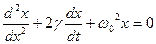
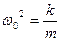
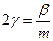
Для того чтобы найти решение уравнения затухающих колебаний рассмотрим уравнение в котором х комплексная величина.
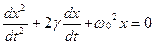
Реальная часть которых = 0
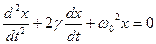
Очевидно, что реальная часть комплексного уравнения является уравнение затухающих колебаний поэтому реальная часть решения комплексного уравнения будет решением уравнения затухающих колебаний.
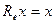
Будем использовать решение уравнения
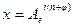
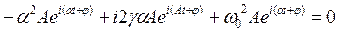
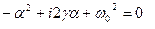
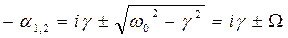
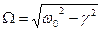
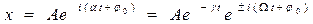
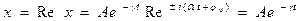
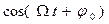

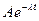 - амплитуда затухающих колебаний.
- амплитуда затухающих колебаний.
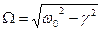 -частота затухающих колебаний
-частота затухающих колебаний
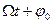 -фаза колебаний
-фаза колебаний
T- в течение которого фаза колебаний меняется на 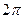 , называется периодом затухающих колебаний.
, называется периодом затухающих колебаний.
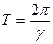
Время в течение которого амплитуда колебаний уменьшается в Е раз, называется временем релаксации
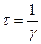
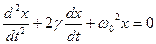
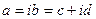
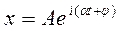
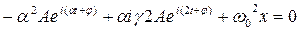

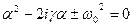
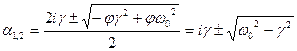
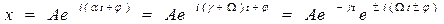
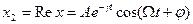

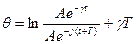
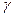 - декремент затухания
- декремент затухания
Заметим, что полученное решение будут справедливо если 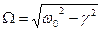 действительная величина, а это возможно если
действительная величина, а это возможно если 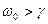 . В этом случае говорят, что система находиться в «периодическом режиме», решим, если
. В этом случае говорят, что система находиться в «периодическом режиме», решим, если 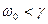 , то
, то
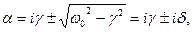 где
где  -действительная величина, тогда
-действительная величина, тогда
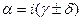
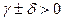 (всегда)
(всегда)
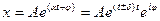
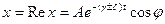
В этом случае никаких колебаний в системе не происходит она просто стремиться к положению равновесия, в зависимости от того какие были начальные условия. В этом случае происходит апериодический режим.
Если 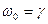 . То режим называется критическим.
. То режим называется критическим.
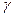 -коэффициент затухания (декремент затухания)
-коэффициент затухания (декремент затухания)
 2014-02-04
2014-02-04 479
479








