Анализ решения. Резонансные характеристики.
Рассмотрим систему на которую действует внешняя сила 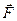 . Если это пружина маятника, то уравнение будет иметь вид:
. Если это пружина маятника, то уравнение будет иметь вид:
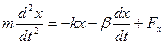
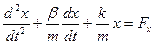
Рассмотрим самый важный случай когда внешняя сила периодична.
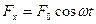
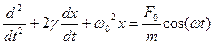
Для того чтобы найти решение этого уравнения рассмотрим комплексное уравнение реальная часть которого совпадает с нашим уравнением.
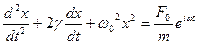
Решение уравнения будем искать в виде:
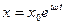
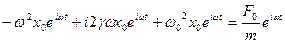
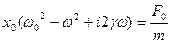
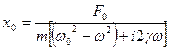
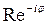
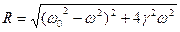
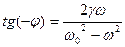
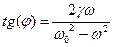
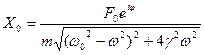

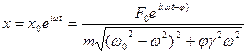
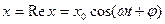 , где
, где
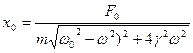
Таким образом найденное решение уравнения вынужденных колебаний представляет собой гармонические колебания амплитуда которых полностью определяется параметрами осциллятора и частотой 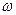 -вынуждающая сила
-вынуждающая сила
Тоже самое касается и начальной фазы колебаний 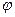 . Другими словами полученное решение независит от начальных условий, а поэтому не является общим и единственным. Это частное решение уравнения вынужденных колебаний.
. Другими словами полученное решение независит от начальных условий, а поэтому не является общим и единственным. Это частное решение уравнения вынужденных колебаний.
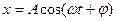
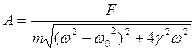
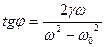
Амплитуда колебаний зависит от параметров системы 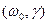 и частотой
и частотой 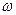 - вынуждающей силы. Зависимость амплитуды от
- вынуждающей силы. Зависимость амплитуды от 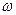 называется амплитудно-частотный характеристикой системы.
называется амплитудно-частотный характеристикой системы.

Такая зависимость называется резонансной, а частота 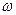 R (при которой амплитуда максимальна) называется резонансной частотой. Если
R (при которой амплитуда максимальна) называется резонансной частотой. Если 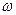 =
=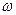 R то говорят, что в системе наблюдается резонанс амплитуд.
R то говорят, что в системе наблюдается резонанс амплитуд.
Для нахождения резонансной частоты нужно приравнять к 0, производную 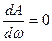
Легко заметить, что достаточно приравнять к нулю производную от подкоренного выражения
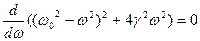
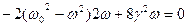
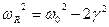
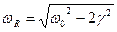
Зависимость базового сдвига 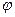 от частоты
от частоты 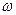 называется фазово-частотной характеристикой.
называется фазово-частотной характеристикой.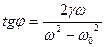
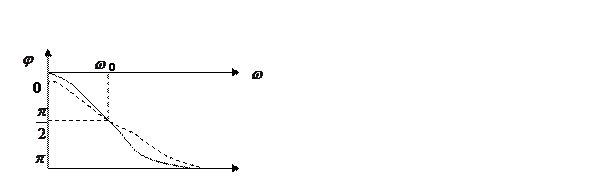
Рассмотрим скорость вынужденных колебаний 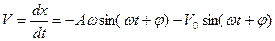
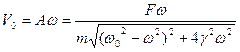 - амплитуда скорости.
- амплитуда скорости.

Полученная зависимость называется резонансом скорости. Для определения частоты при которой V0 = max надо 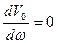 .
.
Полученное решение уравнения вынужденных колебаний представляет собой гармоническое колебание. В §1.3 было показано, что энергия гармонических колебаний постоянна. В §2.4 из 1ой части курса было сказано, что полная энергия системы сохраняется, если сумма мощностей всех не потенциальных сил = 0.
В нашей системе таких сил 2: сила трения и внешняя сила. Как известно мощность силы будет: 
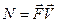
Пусть N- мощность внешних сил 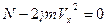
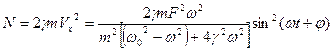
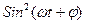 -мощность внешних сил
-мощность внешних сил

Очевидно, что среднее значение мощности вынуждающей силы будет:
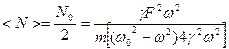

Так как средняя мощность пропорциональна квадрату амплитуды скорости, то резонанс мощности будет происходить при той же частоте, что и резонанс скорости, то есть при 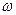 0, осциллятором в котором происходит вынужденные колебания принято характеризовать полимерной
0, осциллятором в котором происходит вынужденные колебания принято характеризовать полимерной 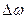 резонансной кривой, которая определяется на уровне половины максимальной средней мощности.
резонансной кривой, которая определяется на уровне половины максимальной средней мощности.
Рассмотрим систему со слабым затуханием когда  , так как при уменьшение затухания ширина резонансной кривой уменьшается, тогда:
, так как при уменьшение затухания ширина резонансной кривой уменьшается, тогда:

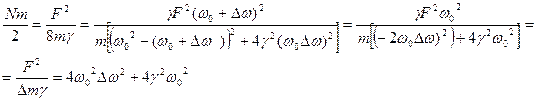
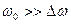
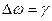
 2014-02-04
2014-02-04 1542
1542
