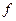Распространение волны в ограниченной среде. Стоячие волны

Рассмотренный одномерный случай в §2.1 было показано, что:

Рассмотрим среду одномерно ограниченную с одной стороны в точке х=0 с нулевым граничным условием:

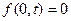
Пусть в такой среде распространяется волна.

Из нулевого граничного условия следует что:

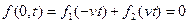
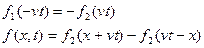
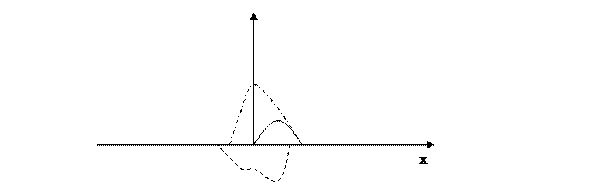
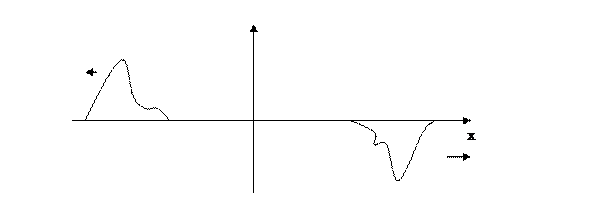
Таким образом при рассмотрение волны в ограниченной среде происходит изменение направления распределения на границе среды. Такое явление называется отражением.

Изменение знака волновой функции в рассмотренном примере связанно исключительно с видом граничного условия.

Рассмотрим гармоническую волну которая распространяется в ограниченной сфере с нулевым граничным условием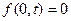

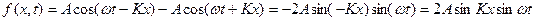
То есть в рассмотренном случаи гармонические возмущения в ограниченной среде никакого распространения волны наблюдаться не будет.

Каждая точка среды будет совершать гармонические колебания с частотой 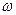и постоянной амплитудой величина которой определяется координатами точки 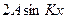. Полученное возмущение называется стоячей волной.

Точки в которых амплитуда колебаний равна нулю называются узлами стоячей волны,

При переходе через узел в стоячей волне фаза колебаний меняется на 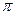. Если среда ограничена с двух сторон нулевыми граничными условиями.

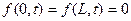тогда:

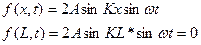
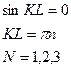
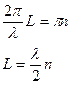
Полученные решение называется собственным модулями колебаний.

Заметим, что в полностью ограниченной среде возможны стоячие волны(собственные моды)лишь с определённой длиной волны (частотой) которая меняется дискретно.