Дифракция Фринеля

Если источник находиться на большом расстояние от экрана с отверстием, а точка наблюдения P также на большом расстояние, то наблюдается дифракция – дифракция Фраунгофера. Если нарушается хотя бы одно из условий то называется дифракция Фринеля.

Фринель дополнил принцем Гюйгенса следующим условие: для того чтобы найти волны в точке p надо разбить поверхность волнового фронта на бесконечно малые плоские участки ds. Тогда волновая функция в точке p будет равна сумме волновой функции излучаемых каждым участком.

Амплитуда в точке p будет равна сумме волны, что совпадает с принципом Гюйгенса.

Амплитуда волны излучаемая каждым участком будет 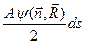А-амплитуда на поверхности волнового фронта

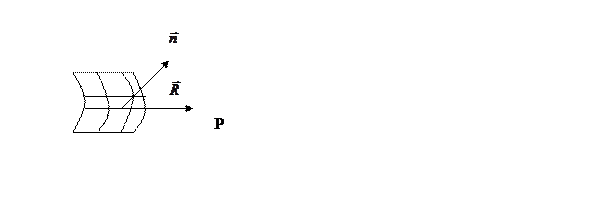
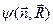- некоторые функции зависят от нормали 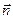и радиуса вектора R, про который известно что она уменьшается с увеличением угла.

В качестве примера принципа Гюйгенса-Фринеля рассмотрим сферически симметрическую задачу когда источник, центр отверстия и точка находятся на одной прямой

Предположим что источник находиться на большом расстояние от отверстия. Тогда волновой фронт в отверстия будет по принципу Фринеля будет равна сумме функций излучения небольшими участками.

Амплитуда колебаний

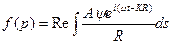
Тогда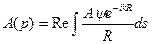

В качеств бесконечно малых участков поверхности ds выберем тонкое кольцо радиусом 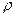и толщиной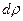

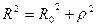
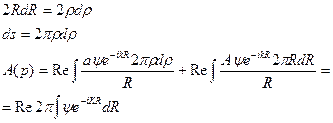
Таким образом амплитуда колебаний в точке p, будет пропорциональной реальной части интервала.

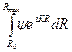
Для вычисления этого интеграла предположим сначала, что 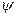постоянна, тогда:

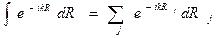
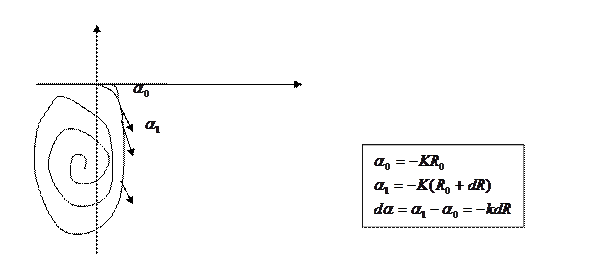
Таким образом предположим, что 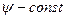то такой интеграл не сходится. Влияние функции 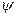приведёт к тому что каждый следующие слагаемое будет меньше предыдущего и в результате окружность деформируется в спираль Фринеля. Если отверстия в экране бесконечно большие то амплитуда колебаний точки p будет определяться радиусом окружности.

Фринель предложил разбить поверхность волнового фронта на зоны(зоны Фринеля) таким образом что расстояние до границ зоны от точки p отличается на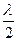

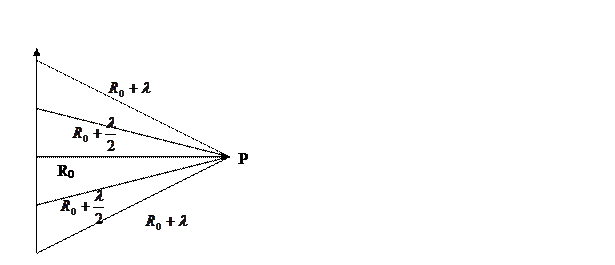
Легко заметить, что в первой зоне Фринеля сответсвует первая полуокружность спирали. Вторая зона Фринеля это вторая полуокружность спирали и тд.

Если отверстие в экране совместимо с размером первой зоны Фринеля то 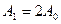то есть в два раза больше чем без экрана, а энергия при этом будет больше в 4 раза.

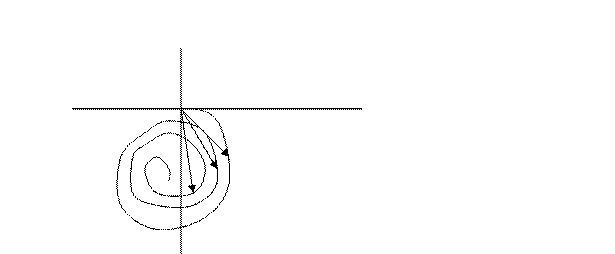
Рассмотрим радиус n-й зоны Фринеля

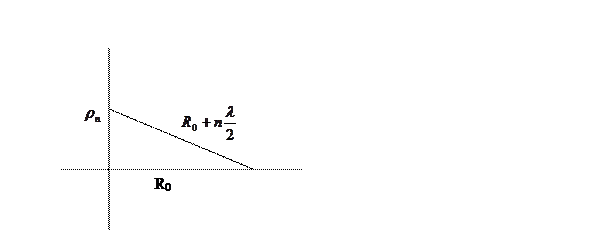
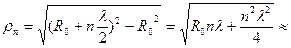
Если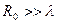

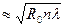
Рассмотрим случай когда точка наблюдения p находиться на очень большом расстояние от экрана с отверстием.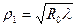будет очень большим и будет много больше отверстия. То есть в отверстие экрана попадает малая часть первой зоны, поэтому амплитуда колебания в точке p будет небольшой. Если точка p будет приближаться к экрану (R₀ уменьшиться) то радиус первой зоны Фринеля будет уменьшаться и в отверстие экрана будет попадать всё больше частиц, то есть А будет увеличиваться, максимальная амплитуда тогда когда радиус первой зоны совпадёт с размером отверстия.

При дальнейшим приближение к экрану в отверстии будет помещаться вторая зона и амплитуда будет убывать.

Когда в отверстие экрана будет помещены обе зоны Фринеля А практически будет равна 0.

§2.9 Волновой пакет.

Рассмотрим 2-е монохроматические волны которые распространяться вдоль оси х с разной частотой и разным волновым вектором.

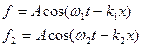
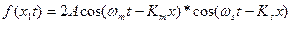
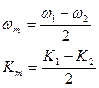
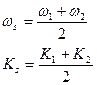
В следующий момент времени вся картина сместиться вдоль оси х причём с разной скоростью будут перемещаться огибающий и наполняющий. Для определения скорости огибающей надо продифференцировать условие постоянства фаз.

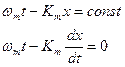
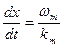
Скорость наполняющей 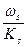. Эти скорости могут не совпадать.

Рассмотрим большое количество монохроматических плоских волн с разной частотой и волновым вектором который растёт вдоль оси х

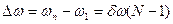
Пусть интервал между соседними волновыми числами тоже одинаков.

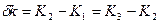
Это возможно в одном единственном случае, когда нет дисперсии, то есть фазовая скорость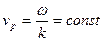

Тогда волновая функция будет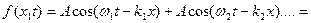

Повторяя выводы §1.7 находим.

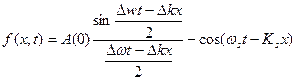
Мы получим волновую функцию амплитуда которой зависит от времени и координаты

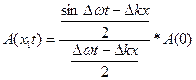
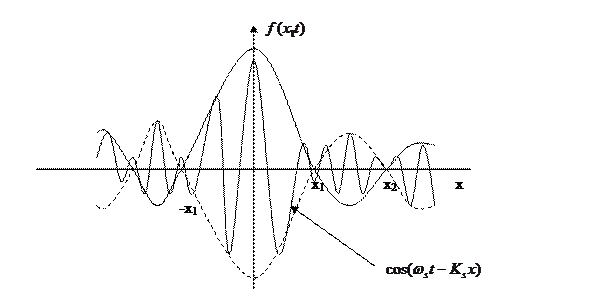
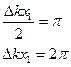
Таким образом при сложение большого числа монохроматических волн с различной частотой мы получим волновую функцию ограниченную в пространстве. Такая волновая функция называется волновым пакетом. За протяженность волнового пакета 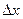выбирают половина расстояния между двумя ближайшими к максимуму нулями.

Протяжённость волнового пакета 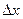и интервал волновых чисел 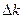образующие его монохроматические волны связанны между собой соотношением 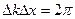.Следует заметить что это равенство получено при определённых условиях.

В общем случае 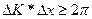Таким образом мы получим, что в результате сложения большого числа монохроматических волн получается ограниченна в пространстве волновая функция. Справедливо и обратное утверждение. Любой произвольный волновой пакет можно представить в виде суммы гармонических волн.

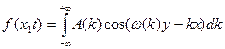
Где 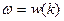- дисперсионное соотношение.

Рассмотрим поведение волнового пакета в следующие моменты времени.

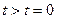все складываемые волны функции сместятся вдоль оси х на одинаковом расстояние так как в отсутствие дисперсии фазовые скорости все одинаковы.

В результате сумма всех волновых функции тоже сместиться на такое же расстояние.

Скорость перемещения волнового пакета будет совпадать с фазовой скоростью волны. При этом очевидно, что форма волнового пакета изменяться не будет.

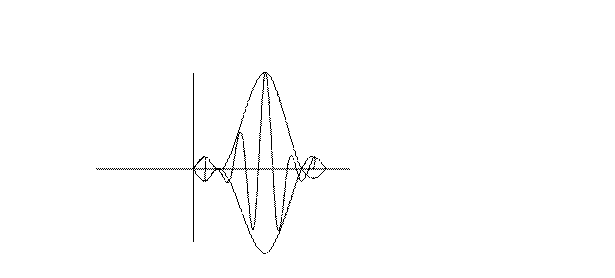
Если фазовые скорости будут различны для разных волн(есть дисперсия) то волновой пакет будет деформироваться при распределении и скорость его движения будет отлична от фазовой скорости.