Модели ограничений

Задачи интервального программирования с линейными ограничениями.

Пусть неизвестны точные значения параметров 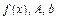порождающей задачи линейного программирования и возможным реализациям этих параметров нельзя приписать функцию распределения внутри известных границ.

Задача интервального программирования имеет вид:

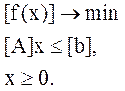
Рассмотрим возможные модели допустимой области

X1 – самая жесткая постановка, X4 – наиболее «либеральная».

Учитывая неотрицательность переменных x>=0, можно выразить множества Xi через граничные элементы интервальной матрицы [A] и интервального вектора [b] (получить детерминированные эквиваленты моделей ограничений)

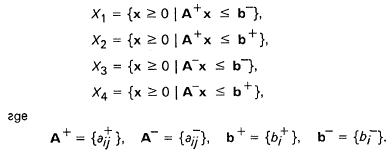
X₅={x>=0: 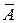x<=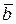}, где 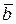=(b⁺+b^-)/2

Из анализа экстремальных допустимых областей следуют включения:

.

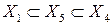Пример.

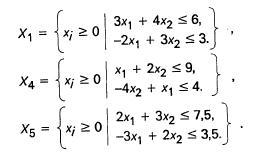
Приведенные выражения позволяют, используя содержательную интерпретацию и технологические требования к допустимому решению определить детерминированную допустимую область задачи в форме одного из множеств 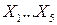, уже не охватывающего интервально заданные параметры.