2014-02-04
1388
1. Сформировать матрицу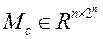 
из векторов 
, задающих вершины гиперпараллелепипеда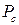 
: 
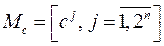. Матрица 
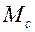определяет конус 
.
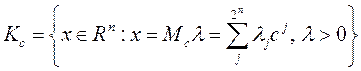2. Берем первый столбец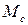 
и находим решение задачи с этим столбцом в качестве градиента
,
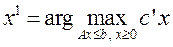- нашли точку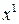 
.
3. В точке 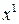формируем матрицу 
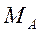, столбцы которой - векторы нормалей активных ограничений (гиперплоскости 
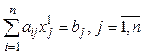). Она задает конус 
.
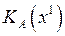4. Решаем матричное уравнение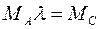 
относительно матрицы 
.
5. Если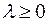 
, то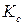 
лежит в 
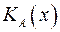, то 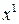- единственное решение.
6. Если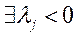 
(это означает, что соответствующие векторы 
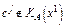, следовательно 
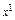неединственное), то для определения множества недоминируемых решений выбираем шаг 7.
Примечание. Если среди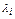 
есть отрицательные, но они соответствуют только ограничениям равенствам, то решение единственно.
7. Выбираем поочередно столбцы матрицы 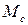и выполняем шаги начиная со 2.
В результате найдем все граничные точки множества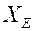 
- множество эффективных и недоминируемых решений.
Пример оптимизации режима обжатия заготовки.(см. лабу)
Решение задач интервального программирования средствами Excel, Mathematica, MathCAD.(см. лабу)
