Алгоритм проверки условия единственности. Графическая иллюстрация.
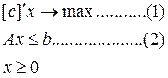
Предположим, что нулевой вектор не принадлежит интервалу:
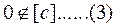
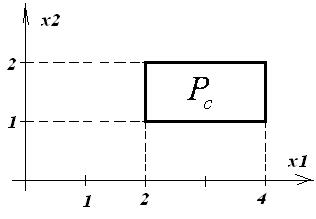
Множество возможных реализаций коэффициентов целевой функции задает в 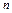 -мерном евклидовом пространстве гиперпараллелепипед
-мерном евклидовом пространстве гиперпараллелепипед 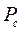 .
.
Пример. 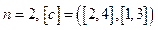
С учетом условия (3) на 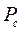 можно потянуть выпуклую коническую оболочку с вершиной в т. 0
можно потянуть выпуклую коническую оболочку с вершиной в т. 0
Обозначим 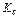 - наименьший выпуклый конус, содержащий
- наименьший выпуклый конус, содержащий 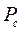 - конус возможных вариаций градиента целевой функции.
- конус возможных вариаций градиента целевой функции.
Возьмем вектор 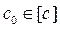 и рассмотрим задачу
и рассмотрим задачу
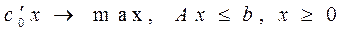 (*)
(*)
- одна из возможных постановок задачи интервального программирования.
Согласно теореме Куна –Таккера, если 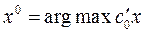 ,
, 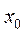 - решение задачи и
- решение задачи и 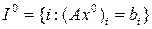 - множество индексов активных в точке
- множество индексов активных в точке 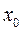 основных ограничений,
основных ограничений, 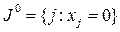 - множество индексов активных в точке
- множество индексов активных в точке 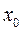 прямых ограничений, то
прямых ограничений, то
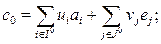
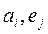 - нормали;
- нормали; 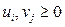 коэффициенты.
коэффициенты.
Т.е. градиент целевой функции можно представить в виде линейной комбинации с неотрицательными коэффициентами нормалей к активным ограничениям в точке  . Значит, градиент
. Значит, градиент 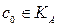 , где
, где 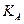 - конус, натянутый на нормали к активным в точке
- конус, натянутый на нормали к активным в точке 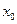 ограничениям.
ограничениям.
|
|
|
Утверждение 2. Пусть 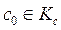 (
(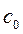 - вектор коэффициентов целевой функции) и пусть
- вектор коэффициентов целевой функции) и пусть 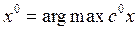 - решение задачи
- решение задачи 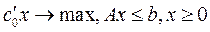 . Тогда если S - множество всех решений задачи (1)-(2), то
. Тогда если S - множество всех решений задачи (1)-(2), то 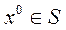 .
.
Доказательство. Для доказательства надо показать, что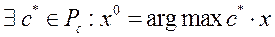 .
.
Заметим, во-первых, что

Покажем теперь, что 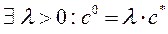 , где
, где  . Так как
. Так как 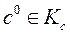 то по определению выпуклой конической оболочки верно, что существует
то по определению выпуклой конической оболочки верно, что существует 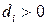 :
: 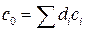 ,
, 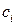 - крайние векторы для конуса
- крайние векторы для конуса 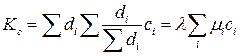 ,
, 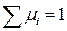 , где
, где 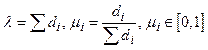 .
.
Так как 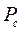 выпукло и
выпукло и 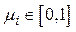 , то
, то 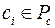 , то
, то 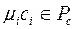 ,
, 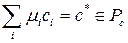 . Получили
. Получили 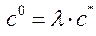 ,
, 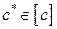 . По условию утверждения
. По условию утверждения  . Отсюда следует
. Отсюда следует 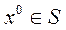 . Утверждение доказано.
. Утверждение доказано.
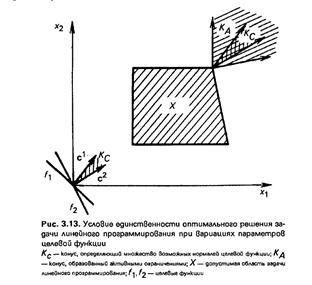 Для определения единственности решения задачи (1) рассмотрим конусы
Для определения единственности решения задачи (1) рассмотрим конусы  и
и 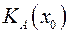 - конус, крайними векторами которого являются векторы нормалей ограничений в точке
- конус, крайними векторами которого являются векторы нормалей ограничений в точке 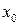 .(см.РИС)
.(см.РИС)
Из условий (2) и свойств задач линейного программирования следует, что  и
и 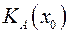 сформировались в
сформировались в 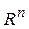 . Оба конуса не зависят от
. Оба конуса не зависят от 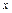 , и поэтому их вершины можно приложить в общую точку.
, и поэтому их вершины можно приложить в общую точку.
Пример. Определение активных ограничений через коэффициенты. Вставить.
Утверждение 3. Если 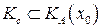 , то любой вектор
, то любой вектор 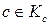 является линейной комбинацией с положительными коэффициентами нормалей к активным ограничениям в точке
является линейной комбинацией с положительными коэффициентами нормалей к активным ограничениям в точке 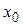 :
: 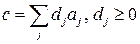 ,
, 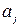 - нормали к активным ограничениям в точке
- нормали к активным ограничениям в точке 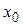 .
.
Доказательство. Следует из определения конусной оболочки, натянутой на векторы нормали.
Теорема. Решение 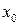 задачи (1)-(2) является единственным, если конус возможных вариаций градиента целевой функции содержится в конусе, натянутом на нормали к активным ограничениям в точке
задачи (1)-(2) является единственным, если конус возможных вариаций градиента целевой функции содержится в конусе, натянутом на нормали к активным ограничениям в точке 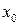 . Т.е. если выполняется следующее включение:
. Т.е. если выполняется следующее включение:
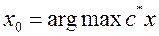 - единственно
- единственно 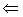
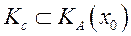 ,
, 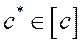 .
.
 2014-02-04
2014-02-04 728
728








