Определение. [С.Н.Черников. Линейные неравенства. Стр.153]
Выпуклым конусом, порожденным конечной системой элементов
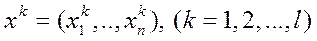
пространства 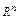 называется множество элементов
называется множество элементов 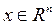 , определяемых формулой
, определяемых формулой
 .
.
При этом элементы 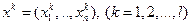 называются образующими элементами конуса.
называются образующими элементами конуса.
Опр. Пусть Х – произвольное множество из 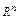 . Конической оболочкой
. Конической оболочкой 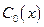 множества
множества 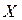 называется множество всех неотрицательных линейных комбинаций
называется множество всех неотрицательных линейных комбинаций
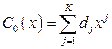
точек 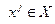 .
.
Коническая оболочка 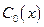 является наименьшим выпуклым конусом, содержащим множество Х.
является наименьшим выпуклым конусом, содержащим множество Х.
Опр. Выпуклый конус К называется многогранным, если он представляет собой коническую оболочку конечного числа своих точек.
Т.о. конус выпуклый, если 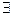 конечное число крайних векторов
конечное число крайних векторов 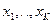 таких что для
таких что для 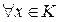 и только для них справедливо, что
и только для них справедливо, что 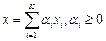 .
.
Еще одно определение многогранного конуса.
Опр. Выпуклый конус 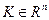 называется многогранным, если для заданного конечного множества векторов
называется многогранным, если для заданного конечного множества векторов 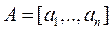 ,
, 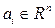 любая точка
любая точка 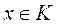 является их неотрицательной линейной комбинацией
является их неотрицательной линейной комбинацией
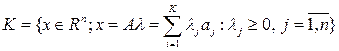
Столбцы матрицы 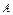 будут крайними векторами.
будут крайними векторами.
Пример: Определить, принадлежит ли вектор 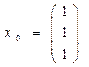 конусу с крайними векторами
конусу с крайними векторами 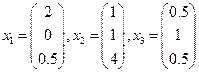
Составим матрицу 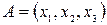 и решим систему
и решим систему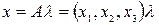
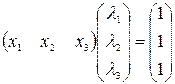 :
: 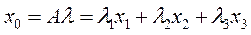 . Решение относительно
. Решение относительно 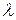 :
:  . Так как
. Так как 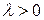 , то
, то 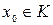 . Да, принадлежит.
. Да, принадлежит.
Еще одно определение конуса.
Множество 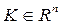 называется конусом с вершиной в т.
называется конусом с вершиной в т. 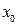 , если из того, что
, если из того, что 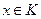 , следует, что множеству К принадлежит и весь луч, выходящий из точки
, следует, что множеству К принадлежит и весь луч, выходящий из точки 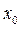 и проходящей через т.
и проходящей через т. 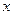 .
.
Т.е. 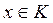 ,
, 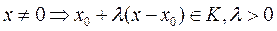 . (1)
. (1)
Точка 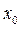 может принадлежать или не принадлежать множеству (1)
может принадлежать или не принадлежать множеству (1)
Утв. К – выпуклый конус с вершиной в точке 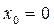 тогда и только тогда, когда из условия
тогда и только тогда, когда из условия 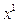 ,
, 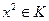 будет следовать, что
будет следовать, что
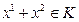 , (2)
, (2)
а также
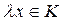 ,
, 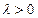 ,
, 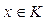 . (3)
. (3)
Док-во. Необх. К – выпуклый конус. Из его определения следует, что если 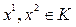 , то
, то 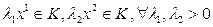 . Возьмем
. Возьмем 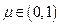 и положим
и положим 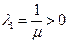 ,
, 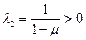 . Получим
. Получим 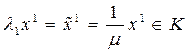 ,
, 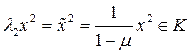 . Т.к. конус выпуклый, то отрезок
. Т.к. конус выпуклый, то отрезок 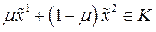
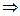
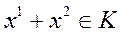 .
.
Дост. Пусть выполнено (2) и (3). Из (3) и (1) следует, что К-конус. Докажем, что он выпуклый. Т.е. если 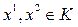 , то
, то
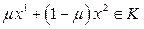 ,
, 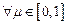 . (4)
. (4)
При 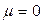 и
и  это очевидно. Докажем для
это очевидно. Докажем для 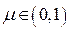 . Рассмотрим точки
. Рассмотрим точки 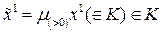 ,
, 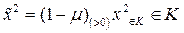 . Тогда
. Тогда 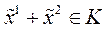 , что совпадает с (4). Утверждение доказано.
, что совпадает с (4). Утверждение доказано.
Опр. Вектор 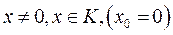 называется крайним для выпуклого конуса
называется крайним для выпуклого конуса 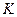 , если из того, что
, если из того, что 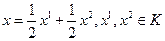 следует
следует 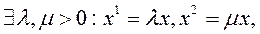 .
.
 2014-02-04
2014-02-04 964
964








