Таблиця 1.
| Робітники | Продуктивність праці, грн./год, на обладнанні | |||
Початковий розподіл можна виконувати довільним способом. Оптимальний розподіл призначень має вигляд
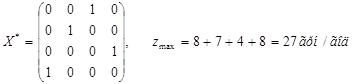 .
.
Розподільчи задачі загального типу.
Загальна розподільча задача ЛП – це розподільча задача, в якій роботи і ресурси (виконавці) виражаються в різних одиницях вимірювання.
Типовим прикладом такої задачі є організація випуску різнорідної продукції на устаткуванні різних типів.
Початкові параметри моделі розподільчої задачі:
· n – кількість виконавців;
· m – кількість видів виконуваних робіт;
· ai – запас робочого ресурсу виконавця 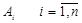 /од. ресурсу/;
/од. ресурсу/;
· bj – план по виконанню роботи 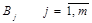 /од. робіт/;
/од. робіт/;
· cij – вартість виконання Bj роботи Ai виконавцем /грн./од. робіт/;
· λij – інтенсивність виконання Bj роботи Ai виконавцем /од.робіт/од.ресурсу/.
Шукані параметри моделі розподільчої задачі:
· xij – планове завантаження виконавця Ai при виконанні Bj робіт /до.ресурсу/;
· 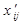 - кількість робіт, які повинен буде провести виконавець Ai /од.робіт/;
- кількість робіт, які повинен буде провести виконавець Ai /од.робіт/;
· L(X) – загальні витрати на виконання всього запланованого об’єму робіт /грн../.
ЕТАПИ ПОБУДОВИ МОДЕЛІ
I.Визначення змінних.
II. Побудова розподільчої матриці (таблиця1).
III.Задання цільової функції.
IV. Задання обмежень.
Таблиця 1.
| Виконавці | Роботи | Запас ресурсу од. ресурсу | |||||||
| B1 | B2 | … | Bm | ||||||
| A1 | λ11 | λ12 | … | λ1m | a1 | ||||
| c11 | c12 | … | c1m | ||||||
| A2 | λ21 | λ22 | … | λ2m | a2 | ||||
| c21 | c22 | … | c2m | ||||||
| … | … | … | … | … | … | ||||
| An | λn1 | λn2 | λnm | an | |||||
| cn1 | cn2 | cnm | |||||||
| План, од. роботи | b1 | b2 | … | bm |
Модель розподільчої задачі
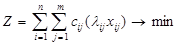
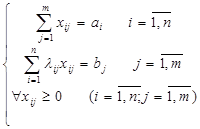 (7)
(7)
де 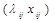 - це кількість робіт j – го виду, i – м виконавцем.
- це кількість робіт j – го виду, i – м виконавцем.
Етапи розв’язання розподільчої задачі
І. Перетворення розподільчої задачі в транпортну задачу:
1. вибір базового ресурсу і розрахунок нормованих продуктивностей ресурсів αi:
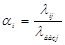
1. перерахунок запасу робочого ресурсу виконавців 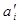 :
:
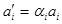 [од. ресурсу];
[од. ресурсу];
2. перерахунок планового завдання 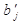 :
:
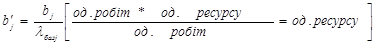
3. перерахунок собівартості робіт:
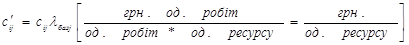
ІІ. Перевірка балансу перерахованих параметрів 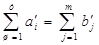 і побудова транспортної матриці.
і побудова транспортної матриці.
ІІІ. Пошук оптимального розв’язку транспортної задачі  .
.
IV. Перетворення оптимального розв’язку транспортної задачі  в оптимальний розв’язок розподільчої задачі, причому перехід виконується за формулою:
в оптимальний розв’язок розподільчої задачі, причому перехід виконується за формулою:
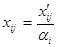 [од. ресурсу],
[од. ресурсу],
де 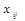 і
і 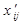 - відповідні елементи розв’язку розподільчої задачі і транспортної задачі.
- відповідні елементи розв’язку розподільчої задачі і транспортної задачі.
V. Визначення кількості робіт, відповідно оптимальному розв’язку розподільчої задачі Х*:
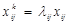
VI. Визначення цільової функції розподільчої задачі Z згідно з (7).
Приклад вирішення задачі типу ТЗ.
На фабриці працюють три типи ткацьких верстатів, які можуть випускати чотири види тканин. Відомі наступні дані про виробничій процес:
· продуктивність верстатів по кожному виду тканин, м/год 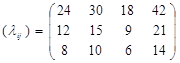
· собівартість тканини, грн./м 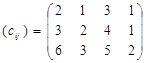
· ресурси робочого часу верстатів (ai): 90, 220, 180 год;
· запланований об’єм випуску тканин (bj): 1200, 900, 1800, 840 м.
Вимагається розподілити випуск тканини по верстатах так, щоб мінімізувати загальну собівартість виробництва тканин.
Питання для самоконтролю.
· Чому транспортну задачу вирішують іншими методами, якщо це задача лінійного програмування?
· Яка транспортна задача називається закритою?
· Що робити якщо транспортна задача відкрита?
· Дайте означення опорного плану транспортної задачі.
· Коли опорний план транспортної задачі не вироджений?
· Що робити, якщо опорний план транспортної задачі вироджений?
· Дайте означення оптимального опорного плану транспортної задачі.
· Сформулюйте необхідні і достатні умови існування розв’язку транспортної задачі.
· Як построїти потенціали строк і стовпців?
· В чому полягає метод північно-західного кута?
· В чому полягає метод найменших витрат?
· Як визначити, що опорний план оптимальний?
· Дайте означення циклу перерозподілу поставок.
Тема 4. Теорія двоїстості та аналіз лінійних моделей оптимізаційних задач.
Лекція 10.
Тема лекції: Двоїста задача лінійного програмування
Мета: ознайомити студентів з методами розв’язання двоїстих задач лінійного програмування, показати взаємозв’язок прямої та двоїстої задач.
План лекції
1. Математичні моделі двоїстих задач.
2. Основні теореми теорії двоістості.
3. Взаємозв’язок розв’язків прямої та двоїстої задач.
Література:
1. Лавріненко Н.М., Латинін С.М., Фортуна В.В., Безкровний О.І. Основи економіко-метематичного моделювання: Навч. Посіб. - Львів: «Магнолія 2006», 2010.- 540с.
2. Іванюта І. Д. Практикум з математичного програмування: Навчальний посібник / І. Д. Іванюта, В. І. Рибалка, І. А. Рудоміно-Дусятська. – К.: «Слово», 2008. - 296 с.
3. Кучма М. І. Математичне програмування: приклади і задачі: Навчальний посібник / М.І. Кучма. – Львів: «Новий Світ - 2000», 2006. - 344 с.
4. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1993. – 336 с.
1 Математичні моделі двоїстих задач.
З кожною задачею лінійного програмування зв’язана деяка інша цілком визначена, задача лінійного програмування яка називається двоїстою.
Початкова задача називається прямою задачею ЛП. Ці дві задачі тісно пов’язані між собою і утворюють єдину пару двоїстих задач.
Якщо пряма задача ЛП має вигляд:
Z=∑cixi →max (1)
за умов
∑aijxj ≤bi, (i=1,2…..m) (2)
xj ≥0 (j=1,2…..n) (3)
то двоїста задача записується так:
F=∑biyi →min (1*)
за умов
∑aijyi≥ cj, (j=1,2…..n) (2*)
yi≥0 (i=1,2…..m) (3*)
В матричному вигляді їх можна представити таким чином:
Пряма задача
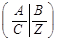 , xj ≥0 (j=1,2…..n)
, xj ≥0 (j=1,2…..n)
де А – матриця системи обмежень задачі розміром m x n;
В – вектор стовпець;
С – вектор строка;
АХ≤В;
Z →max.
Двоїста задача
tr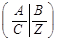 =
=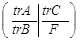 , yi ≥0 (i=1,2…..m)
, yi ≥0 (i=1,2…..m)
де trA – транспонована матриця А;
trС – транспонований вектор С;
trB - транспонований вектор В;
AY ≥trC;
F →min.
У несиметричних парах двоїстих задач обмеження прямої задачі можуть бути записані як рівняння (у канонічному вигляді), а двоїстої – лише як нерівності. Якщо у цільовій функції двоїстої задачі вимагається знайти мінімум, то система обмежень матиме знак «≥», якщо максимум, то знак «≥».
Моделі несиметричних пар цих задач можна зобразити у вигляді:
| Пряма задача | Двоїста задача |
| Z=∑cixi →max/min за умов ∑aijxj =bi, (i=1,2…..m) xj ≥0 (j=1,2…..n) | F=∑biyi →min/max за умов ∑aijyi≥/≤ cj, (j=1,2…..n) yi є(-∞,∞) (i=1,2…..m) |
Математична модель прямої задачі мішаної пари двоїстих задач містить обмеження, записані як рівняння, так і нерівності, причому знаків різних, за виглядом. Для складання двоїстої задачі необхідно привести всі нерівності системи обмежень прямої задачі до одного вигляду: якщо пряма задача на максимум, то всі нерівності обмежень приводимо до вигляду «≤», якщо на мінімум до вигляду «≥». Нерівності, для яких дані вимоги не виконуються, домножимо на (-1).
2. Основні теореми двоїстості.
Розглянемо пару даоїстих задач, утворену канонічною задачею ЛП і двоїстої до неї:
Пряма:
Z=∑cixi →max/min
за умов
∑aijxj =bi, (i=1,2…..m)
xj ≥0 (j=1,2…..n)
Двоїста:
F=∑biyi →min/max
за умов
∑aijyi≥/≤ cj, (j=1,2…..n)
yi є(-∞,∞) (i=1,2…..m)
Між прямою і двоїстою задачами ЛП існує тісний взаємозв’язок, який видно з наведених далі лем та теорем.
Лема 1. Якщо Х – деякий план прямої задачі, Y – довільний план двоїстої задачі, то значення цільової функції прямої задачі при плані Х не перевищує значення цільової функції двоїстої задачі при плані Y, тобто
Z(X)≤F(Y)
Лема 2. Якщо Z(X*)=F(Y*), та X* - оптимальний план прямої задачі, то Y* - оптимальний план двоїстої задачі.
Теорема 1. (перша теорема двоїстості). Якщо одна із пар двоїстих задач має оптимальний план, то і друга задача має оптимальний план і значення цільової функції при їх оптимальних планах рівні між собою, тобто Z(X*)=F(Y*).
Якщо ж цільова функція однієї із двоїстих задач необмежена (для прямої задачі - зверху, а для двоїстої з низу), то множина планів двоїстої задачі є порожньою.
Теорема 2. (друга теорема двоїстості). Для того щоб плани Х* і Y* відповідно до задач (1) – (3) і (1*) – (3*) були оптимальними планами цих задач, необхідно і достатньо, щоб для кожного j (j=1,2…..n) виконувалась рівність:
(a1j(y1)* + a2j(y2)* + ……. + amj(ym)* - cj)(xj)* = 0
Економічну інтерпретацію двоїстої задачі розглянемо на прикладі задачі про оптимальне використання ресурсів, математична модель якої має вигляд:
Z=∑cixi →max
за умов
∑aijxj =bi, (i=1,2…..m)
xj ≥0 (j=1,2…..n)
Двоїста задача до неї буде така:
F=∑biyi →min
за умов
∑aijyi≥ cj, (j=1,2…..n)
yi ≥0 i=1,2…..m
Приклад. Підприємство виготовляє три види продукції А,В,С.
Дані задачі приведені у таблиці:
| Види сировини | Норми витрат сировини (кг) | Запаси сировини | ||
| А | В | С | ||
| S1 | ||||
| S2 | ||||
| S3 | ||||
| Ціна від реалізації 1-ї одиниці продукції |
Знайти такий план випуску продукції, щоб прибуток від їх реалізації був максимальним.
3 Взаємозв’язок розв’язків прямої та двоїстої задач.
Розглянемо пару двоїстих задач ЛП (1) – (3) і (1)* - (3)*, пряма задача якої записана у канонічному вигляді. Наступна теорема встановлює взаємозв’язок між розв’язками прямої і двоїстої задачами.
Теорема 3. Якщо пряма задача ЛП має оптимальний план Х*, отриманий симплекс методом, то оптимальний план Y* двоїстої задачі визначається за формулою:
Y*=CбазР-1 (4)
де Cбаз – вектор рядок, що складається з коефіцієнтів цільової функції прямої задачі при невідомих, які є базисними в оптимальному плані; Р-1 – матриця, обернена до матриці Р, складеної з компонент базисних векторів оптимального плану задачі.
Таким чином, якщо знайти симплекс методом оптимальний план задачі (1) –(3), то використовуючи останню симплекс таблицю, можна визначити Cбаз і Р-1 та за допомогою співвідношення (5.4), знайти план двоїстої задачі.
Відмітимо, що існує взаємно-однозначна відповідність між змінними: основним змінним прямої задачі відповідають додаткові змінні двоїстої задачі і навпаки:
| Змінні прямої задачі | |||||||
| Основні | Додаткові | ||||||
| Х1 | Х2 | …….. | Хк | Хк+1 | Хк+2 | ………. | Хn |
| Yn-k+1 | Yn-k+2 | …….. | Yn | Y1 | Y2 | ……… | Yn-k |
| Додаткові | Основні | ||||||
| Змінні двоїстої задачі |
Ідея двоїстого симплексного методу полягає у зв’язку між розв’язуваннями прямої та двоїстої задач ЛП. Немає потреби окремо розв’язувати пряму задачу, а окремо двоїсту, оскільки розв’язок обох задач можна знайти за одними й тими самими симплекс таблицями, пам’ятаючи, що невідомим прямої задачі відповідають стовпчики таблиці, а невідомим другої – рядки таблиці.
Двоїстий симплекс метод використовується для знаходження розв’язку задачі ЛП, записаної у канонічному вигляді, для якої серед векторів Рj, складених з коефіцієнтів при невідомих у системі рівнянь, є рівно m одиничних.
Також цей метод можна використовувати для знаходження розв’язку задач ЛП, коли вільні члени системи рівнянь є довільними числами (для розв’язування задач симплекс методом числа bi припускались невід’ємними).
Питання для самоконтролю.
· Нехай є задача про оптимальне використання ресурсів. Дайте економічну інтерпретацію двоїстої задачі.
· Сформулюйте першу теорему двоїстості.
· Сформулюйте другу теорему двоїстості.
· Перечисліть ознаки взаємно двоїстих задач.
· Як по рішенню прямої задачі знайти рішення двоїстої задачі.
· В чому полягає ідея двоїстого симплекс методу.
· Який економічний зміст основних змінних двоїстої задачі?
· Який економічний зміст додаткових змінних двоїстої задачі?
· Який економічний зміст перевірки системи обмежень прямої задачі для знайденого оптимального плану?
· Що дає перевірка обмежень двоїстої задачі?
· Як проводиться аналіз стовбців останньої симплекс таблиці, для яких Δi>0?
Тема 5. Цілочислові та параметричні задачі лінійного програмування
Лекція 11.
Тема лекції: Узагальнення задачі лінійного програмування.
Мета: ознайомити студентів з методами розв’язання задач цілочислового та параметричного програмування.
План лекції
1. Задачі цілочислового програмування.
1. Метод Гоморі.
2. Параметричне лінійне програмування.
Література:
1. Лавріненко Н.М., Латинін С.М., Фортуна В.В., Безкровний О.І. Основи економіко-метематичного моделювання: Навч. Посіб. - Львів: «Магнолія 2006», 2010.- 540с.
2. Іванюта І. Д. Практикум з математичного програмування: Навчальний посібник / І. Д. Іванюта, В. І. Рибалка, І. А. Рудоміно-Дусятська. – К.: «Слово», 2008. - 296 с.
3. Кучма М. І. Математичне програмування: приклади і задачі: Навчальний посібник / М.І. Кучма. – Львів: «Новий Світ - 2000», 2006. - 344 с.
4. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1993. – 336 с.
Задачі цілочислового програмування.
Безліч економічних завдань вимагають цілочисельного рішення. До них належать завдання, у яких змінні величини означають кількість одиниць неподільної продукції (кількість верстатів при установці устаткування, розподіл судів по лініях, літаків по рейсам, обчислювальних машин в керуючому комплексі і т.д.).
У математичній моделі задачі цілочислового програмування як цільова функція так і система обмежень можуть бути лінійними, нелінійними і змішаними.
Ми будемо розглядати тільки лінійні задачі цілочислового лінійного програмування.
Задача цілочислового програмування формулюється так:
Z= 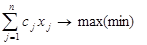 (1)
(1)
за умов
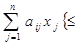 ,=
,=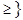 bi, i=
bi, i= , (2)
, (2)
xj≥0, (j=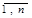 ), (3)
), (3)
xj - цілі, (j=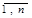 ), (4)
), (4)
умова цілочисельності (4), яка додається до звичайної задачі ЛП, суттєво ускладнює її розв’язання.
2. Метод Гоморі.
Сутність методу Гоморі (метод відтинання) полягає у тому, що спочатку розв’язується звичайна задача ЛП без урахування вимог цілочисельності змінних. Якщо отриманий оптимальний план задачі цілочисловий, то задача розв’язана. У протилежному випадку у модель вводиться спеціальне додаткове обмеження, що враховує цілочисельність змінних і володіє такими властивостями:
- вона повинна бути лінійною;
- вона повинна відтинати знайдений оптимальний нецілочисловий план задачі;
- не повинна відтинати ні одного цілочислового плану.
Додаткове обмеження, що має перелічені вище властивості, називається правильним відтинанням.
Це додаткове обмеження вводиться до оптимального плану якщо серед компонент оптимального є число з дробовую частиною. На базі цієї змінної будується додаткове обмеження Р.Гоморі:
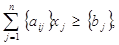
де  - дробова частина числа,
- дробова частина числа,
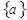 =а-[a].
=а-[a].
[a] – ціла частина числа а, т.б. найбільше ціле число, яке не перевищує числа а.
Якщо оптимальний план задачі має де кілька дробових значень, то додаткову нерівність складають для тієї змінної яка має найбільшу дробову частину.
Геометричний зміст кожного лінійного додаткового обмеження відповідає проведенню прямої (гіперплощини), яка відтинає від многокутника допустимих розв’язків деяку його частину разом із оптимальним нечисловим планом. Причому не відтинаються точки з цілими координатами цієї області допустимих розв’язків. У результаті область допустимих розв’язків послабленої задачі поступово зменшується доти, доки всі змінні оптимального плану не набувають цілочислових значень.
Розглянемо метод Гоморі на прикладі.
Приклад 1.
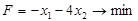
за умов
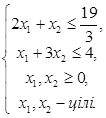
3. Параметричне лінійне програмування.
Параметричне програмування являє собою один з розділів математичного програмування, вивчає завдання, в яких цільова функція або обмеження залежать від одного або кількох параметрів.
Необхідність розгляду подібних завдань обумовлена різними причинами. Однією з основних є та, що вихідні дані для чисельного рішення будь-якої реальної задачі оптимізації в більшості випадків визначаються наближено або може змінюватися під впливом якихось чинників, що може істотно позначитися на оптимальності вибираної програми (плану) дій. Відповідно, розумно вказувати не конкретні дані, а діапазон можливої зміни даних, що б в результаті рішення мати найкращі плани для будь-якого варіанту вихідних даних.
З математичної точки зору параметричне програмування виступає як один із засобів аналізу чутливості рішення до варіації вихідних даних, оцінки стійкості рішення.
Зауважимо, що існують різні підходи до подібного аналізу (наприклад, на основі постановки двоїстої задачі). Тут ми, не посилаючись на двоїсті оцінки, розглянемо найпростіші варіанти рішення для самих найпростіших параметричних задач.
Розглянемо задачу параметричного лінійного програмування, в якій тільки коефіцієнти цільової функції лінійно залежать від деякого єдиного параметра λ (часу, температури і т. п.):
Відшукати максимум (або мінімум) функції:
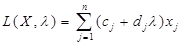
за умов
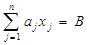
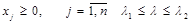
Якщо звернутися до геометричної інтерпретації задачі, то можна помітити, що вектор-градієнт лінійної форми визначається її параметром. Наприклад, для цільової функції L (х, λ) = λх1 + (1-λ) х2 при різних значеннях параметра λ градієнт визначає різні напрямки зростання функції.
Неважко бачити, що, якщо при деякому значенні параметра максимум досягається в вершині A, то невелика варіація цього значення дещо змінить напрямок градієнта, але не змінить положення точки максимуму. Звідси напрошується висновок, що деякий план, оптимальний при λ = λ0 оптимальний і в околиці λ0, тобто при α ≤ λ ≤ β де λ0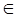 [α, β].
[α, β].
Можна помітити, що при градієнті, що став перпендикулярним деякої сторони багатокутника планів, маємо два різних оптимальних опорних плани з одним і тим же значенням лінійної форми, звідки можна стверджувати безперервність екстремуму лінійної форми за λ.
У разі необмеженість безлічі планів можна стверджувати, що якщо лінійна форма не обмежена при λ = λ0, то вона не обмежена при всіх λ, більших або менших λ0.
Алгоритм для вирішення завдань параметричного лінійного програмування в разі залежності від параметра коефіцієнтів цільової функції незначно відрізняється від звичайного симплексного методу.
У разі залежності від параметра компонент вектора правих частин обмежень, тобто рішення задачі пошуку екстремуму функції
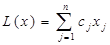
за умов
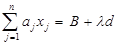
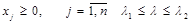
Приклад 2.
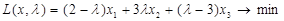
за умов
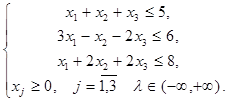
Приклад 3.
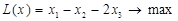
за умов
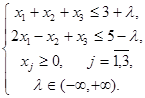
Для того щоб вирішити задачу, достатньо вирішити двоїсту задачу до неї, яка має вигляд
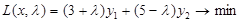
за умов
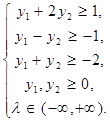
Питання для самоконтролю.
· В чому суть методу Гоморі?
· Як составити додаткове обмеження, якщо компоненти оптимального плану дробові?
· В якому випадку задача ЦЛП не має рішення?
· Який геометричний смисл має додаткове обмеження?
· Яке відтинання є правільним?
· Сформулюйте параметричну задачу, параметр якої присутній у функції цілі.
· Сформулюйте параметричну задачу, параметр якої присутній у системі обмежень.
· Вкажіть на взаємозв’язок параметричної задачі та стійкості рішень задачі ЛП.
· Вкажіть взаємозв’язок параметричної задачі на чутливість рішень задачі ЛП.
Тема 6. Елементи теорії ігор
Лекція 12.
Тема лекції: Матричні ігри
Мета: ознайомити студентів з методами розв’язання задач теоріі ігор та зведення їх до задач ЛП.
План лекції
1. Постановка задач теорії парних ігор з нульовою сумою.
2. Задачі з сідловою точкою. Задачі в чистих стратегіях.
3. Ігри в мішаних стратегіях.
Література:
1. Лавріненко Н.М., Латинін С.М., Фортуна В.В., Безкровний О.І. Основи економіко-метематичного моделювання: Навч. Посіб. - Львів: «Магнолія 2006», 2010.- 540с.
2. Іванюта І. Д. Практикум з математичного програмування: Навчальний посібник / І. Д. Іванюта, В. І. Рибалка, І. А. Рудоміно-Дусятська. – К.: «Слово», 2008. - 296 с.
3. Кучма М. І. Математичне програмування: приклади і задачі: Навчальний посібник / М.І. Кучма. – Львів: «Новий Світ - 2000», 2006. - 344 с.
4. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1993. – 336 с.
1. Постановка задач теорії парних ігор з нульовою сумою.
На практиці дуже часто виникають ситуації, коли необхідно приймати рішення в умовах невизначеності, тобто в умовах, коли дві або більш сторін мають на меті різні цілі, но результат для кожної із сторін залежить від дій супротивника. Наприклад, гра в шахи, шашки і т.д. В економіці конфліктні ситуації зустрічаються дуже часто: продавець і покупець, банк і клієнт, постачальник і споживач.
В 1944 році з’явилася математична дисципліна – теорія ігор, основою для якої стала монографія американського економіста Неймана.
Теорія ігор – це теорія математичної моделі конфліктних ситуацій, інтереси гравців котрих різні і кожний з них досягає своєї цілі (мети) різними шляхами.
Результат гри є виграшем для одних і програшем для других.
Означення 1. Модель любої конфліктної ситуації зветься грою.
Означення 2. В процесі гри кожний гравець висуває власну стратегію. Стратегія гравця – сукупність правил, по котрих при кожному ході відбувається вибір певних дій. Цей вибір залежить від сформованих обставин.
Означення 3. гра зветься парною, якщо в ній беруть участь дві сторони.
Означення 4. Кількісна оцінка результатів гри зветься платою.
Означення 5. Парна гра зветься грою з нульовою сумою, якщо програш одного є виграшем іншого.
Означення 6. Стратегія гравця називається оптимальною, якщо при повторенні гри вона забезпечує гравцю максимально можливий середній виграш (або теж само- мінімально можливий середній програш).
1. Задачі з сідловою точкою. Задачі в чистих стратегіях.
Розглянемо парну гру:
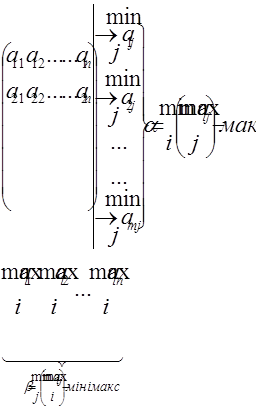
Приклад 1. Задана платіжна матриця А парної гри з нульовою сумою: А=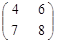 . Знайти ціну гри, сідлову точку гри.
. Знайти ціну гри, сідлову точку гри.
Приклад 2..Задана платіжна матриця А парної гри з нульовою сумою: А=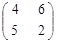 . Знайти верхнью та нижню ціну гри.
. Знайти верхнью та нижню ціну гри.
Ігри в мішаних стратегіях. Основна теорема теорії ігор.
Якщо немає сідловок точки, то гра ведеться в мішаних стратегіях, тобто розглядається не вибір можливої стратегії, а ймовірність з котрою обирається ця стратегія. Мішана стратегія визначається сукупністю ймовірностей різних стратегій.
Нехай гравець А для визначення своєї мішаної стратегії використав метод випадкового вибіру.
Нехай х1 – ймовірність вибору 1-ої стратегії;
х2 - ймовірність вибору 2-ої стратегії;
…………………………………………………
xm - ймовірність вибору m-ої стратегії.
Означення 1. Мішаною стратегією гравця А називається упорядкований набір m чисел х1, х2, ….., xm, які задовольняють умовам: 0≤xi≤1, i=
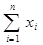 =1.
=1.
Мішані стратегії гравців А та В позначають 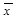 =(x1,x2, …, xm),
=(x1,x2, …, xm), 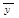 =(y1,y2,…,yn).
=(y1,y2,…,yn).
Всяка матрична гра з нульовою сумою має оптимальне рішення в мішаних стратегіях, при цьому відхилятися гравцям від цих стратегій не вигідно.
Теорема. О методі знаходження рішення.
Для того, щоб число ν було ціною гри, а Х* та Y* - оптимальними стратегіями, необхідно та достатньо, щоб виконувались умови:
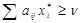 j=
j=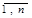
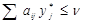 i=
i=
Визначення оптимальних стратегій та ціни гри створюють процес знаходження рішення гри.
Теорема 2. Якщо один з гравців використовує мішану оптимальну стратегію, то його виграш дорівнює ціні гри ν незалежно від того, з якими частотами буде використовувати другий гравець стратегії, які вийшли до оптимальної стратегії(в тому числі і чисті стратегії).
Розглянемо гру з платіжною матрицею 2х2: A=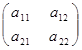 .
.
Якщо сідлової точки нема, рішення гри є мішані стратегії 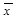 =(х1,х2) та
=(х1,х2) та 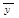 =(y1,y2) стратегії гравців А та В, для котрих ймовірністі xi yi відмінні від нуля, звуться активними.
=(y1,y2) стратегії гравців А та В, для котрих ймовірністі xi yi відмінні від нуля, звуться активними.
Стратегію гравця А шукаємо по формулі ХА=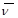 , де Х=(х1,х2),
, де Х=(х1,х2), 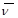 =(ν, ν).
=(ν, ν).
До даної системи рівнянь додаємо норміровочне рівняння х1+х2=1.
Для гравця В:
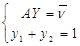
де Y=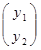 ,
, 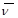 =
=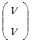 .
.
Розв’язавши систему рівнянь знайдемо оптимальні стратегії гравців та ціну гри ν.
Наслідок. Для того, щоб х*, була оптимальною мішаною стратегією матричнох гри з матрицею А та ціною гри ν, необхідно та достатньо, щоб виконувались наступні нерівності:
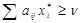 j=
j=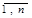
Аналогічно для гравця В: Для того, щоб у* була оптимальною мішаною стратегією матричної гри з матрицею А та ціною гри ν, необхідно та достатньо, щоб виконувались наступні нерівності:
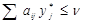 i=
i=
Таким чином, для розв’язування гри необхідно визначити стратегії, що задовольняють вишенаведані системи обмежень та умови нормування:
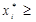 0,
0, 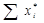 =1, i=
=1, i= ,
, 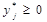 ,
, 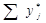 =1, j=
=1, j=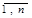 .
.
Цей наслідок дозволяє сформулювати для розв’язання гри пару задач лінійного програмування.
Тема 6. Елементи теорії ігор
Лекція 13.
Тема лекції: Матричні ігри (продовження)
Мета: ознайомити студентів з методами розв’язання задач теоріі ігор та зведення їх до задач ЛП.
План лекції
2. Графічний метод розв’язання задач теорії ігор.
3. Зведення задач теорії ігор до задач ЛП.
4. Зведення задачі ЛП до матричної гри.
Література:
1. Лавріненко Н.М., Латинін С.М., Фортуна В.В., Безкровний О.І. Основи економіко-метематичного моделювання: Навч. Посіб. - Львів: «Магнолія 2006», 2010.- 540с.
2. Іванюта І. Д. Практикум з математичного програмування: Навчальний посібник / І. Д. Іванюта, В. І. Рибалка, І. А. Рудоміно-Дусятська. – К.: «Слово», 2008. - 296 с.
3.Кучма М. І. Математичне програмування: приклади і задачі: Навчальний посібник / М.І. Кучма. – Львів: «Новий Світ - 2000», 2006. - 344 с.
1. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1993. – 336 с.
4. Графічний метод розв’язання теорії ігор.
Графічний метод можна застосовувати до ігор, в яких хоча б один гравець має тільки дві стратегії, тобто до ігор 2xn i mx2.
Основні етапи розв’язку ігор 2xn i mx2:
· Будуємо прямі, що відповідають стратегіям другого (першого) гравця.
· Визначаємо нижню (верхню) межу виграшу.
· Знаходимо дві стратегії другого (першого) гравця, яким відповідають дві прямі, що перетинаються в точці з найбільшою (найменшою) ординатою.
· Визначаємо ціну гри і оптимальні стратегії.
Приклад 3. Знайти розв’язок гри заданої матрицею
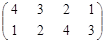
5. Зведення задач теорії ігор до задач ЛП.
Якщо один з гравців застосовує свою оптимальну стратегію х*, то інший не може покращити своє становище, тобто для оптимальної стратегії справедливі співвідношення:
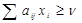 j=
j=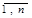 , xi≥0,
, xi≥0, 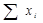 =1, i=
=1, i= за умов ν→Мах.
за умов ν→Мах.
Перетворимо цю задачу, здійснивши підстановку pi=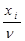 , і отримаємо
, і отримаємо
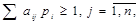
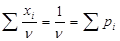 →Min,тому що ν→Мах.
→Min,тому що ν→Мах.
Таким чином, маємо задачу ЛП, розв’язуючи яку, отримаємо значення pi, за допомогою яких шляхом оберної підстановки визначимо оптимальні значення ймовірностей, що складають оптимальну мішану стратегію.
А здійснивши підстановку qj=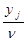 і враховуючи, що гравець В прагне мінімізувати програш, отримаємо пару двоїстих задач ЛП, розв’язання яких дозволить визначити оптимальні стратегії гравців А та В:
і враховуючи, що гравець В прагне мінімізувати програш, отримаємо пару двоїстих задач ЛП, розв’язання яких дозволить визначити оптимальні стратегії гравців А та В:
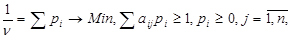
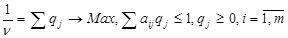 .
.
Таким чином, процедура розв’язування гри двох осіб є наступною:
1. Розраховуємо нижню та верхню ціну гри; якщо вони рівні між собою, то гра розв’язана.
2. Спрощуємо гру шляхом виключення домінованих стратегій.
3. Формулюємо пару задач ЛП, розв’язавши одну з яких, встановлюємо оптимальну мішану стратегію одного з гравців (зручніше гравця В).
4. За розв’язком прямої задачі знаходимо розвязок двоїстої задачі.
5. Шляхом оберненої підстановки визначемо оптимальні стратегії для спрощеної гри та доповнюємо їх домінованими чистими стратегіями з ймовірністю використання, що рівні нулю.
Приклад 4. Підприємство виготовляє три види продукції А1, А2, А3, отримуючи при цьому прибуток, що залежить від попиту. Попит може перебувати в одному з чотирьох станів В1, В2, В3, В4. Прибуток підприємства, який отриманий при виготовленні кожного виду продукції в залежності від попиту, наведено у таблиці 1. Визначити оптимальні обсяги виготовлення продукції, що гарантують середню величину прибутку при будь-якому попиті, вважаючи його невизначеним.
Таблиця 1.
| В1 | В2 | В3 | В4 | |
| А1 | ||||
| А2 | ||||
| А3 |
Зведення задачі ЛП до матричної гри.
Якщо пряма задача ЛП має вигляд:
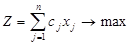
за умов
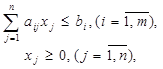
то матрична гра визначається платіжною матрицею порядку 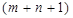 вигляду:
вигляду:
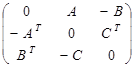 ,
,
де А – матриця коефіцієнтів при невідомих системи обмежень задачі ЛП; В – матриця вільних членів; С – матриця коефіцієнтів при невідомих цільової функції, індекс Т означає операцію транспонування.
Якщо задача ЛП має вигляд:
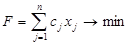
за умов
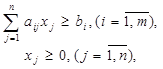
То матрична гра задається платіжною матрицею порядку 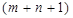 вигляду:
вигляду:
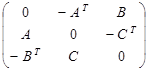
Зауважемо, що якщо кожна матрична гра має оптимальні стратегії, то не всяка задача ЛП має розв’язки.
Приклад 5. Побудувати гру задану задачею ЛП:
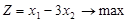
за умов
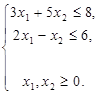
Питання для самоконтролю.
· Дайте визначення гри двох осіб з нульовою сумою.
· Дайте визначення сідловок точки.
· Дайте визначення середнього виграшу.
· Що таке чиста стратегія?
· що таке мішана стратегія?
· Що таке домінована стратегія?
· Сформулюйте основну теорему теорії ігор для двох осіб.
· Як звести задачу теорії ігор до задачі ЛП?
· Як звести задачу ЛП до задачі теорії ігор?
Тема 7. Нелінійні оптимізаційні моделі економічних систем
Лекція 14.
Тема лекції: Задача дробово-лінійного програмування
Мета: ознайомити студентів з методами розв’язання задач дробово-лінійного програмування та зведення їх до задач ЛП.
План лекції
1. Постановка задачі дробово-лінійного програмування.
2. Приведення задачі дробово-лінійного програмування до задач ЛП.
3. Розв’язання задач дробово-лінійного програмування.
4. Графічне розв’язання задачі дробово-лінійного програмування.
Література:
1. Лавріненко Н.М., Латинін С.М., Фортуна В.В., Безкровний О.І. Основи економіко-метематичного моделювання: Навч. Посіб. - Львів: «Магнолія 2006», 2010.- 540с.
2. Іванюта І. Д. Практикум з математичного програмування: Навчальний посібник / І. Д. Іванюта, В. І. Рибалка, І. А. Рудоміно-Дусятська. – К.: «Слово», 2008. - 296 с.
3. Кучма М. І. Математичне програмування: приклади і задачі: Навчальний посібник / М.І. Кучма. – Львів: «Новий Світ - 2000», 2006. - 344 с.
4. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1993. – 336 с.
Постановка задачі дробово-лінійного програмування.
Серед оптимізаційних задач велике значення мають задачі, у яких необхідно знайти екстремальні значення економічних показників, які є відносними величинами. У таких задач умови обмеження нічим не відрізняються від умов обмежень у задачах лінійного програмування, але цільова функція являє собою дріб, у якому чисельник і знаменник представляють собою лінійні функції від змінних 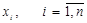 де хi – компоненти оптимального плану.
де хi – компоненти оптимального плану.
Математична модель задачі дробово-лінійного програмування може бути використана для визначення рентабельності виробництва, витрат розрахункових на грошову одиницю продукції, собівартості продукції, продуктивності праці тощо.
Загальна постановка задачі дробово-лінійного програмування записується так:
Знайти такі значення змінних 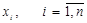 , які задовольняють системі обмежень:
, які задовольняють системі обмежень:
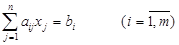 (1)
(1)
умовам
 (2)
(2)
при яких цільова функція
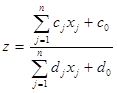 (3)
(3)
досягає максимуму (мінімуму).
Задача (1)-(3) являє собою задачу нелінійного програмування, тому що цільова функція z не є лінійною функцією змінних 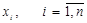 . Виконавши відповідні перетворення змінних (заміну змінних) задачу можна привести до задачі лінійного програмування й скористатися для її розв’язання симплекс-методом.
. Виконавши відповідні перетворення змінних (заміну змінних) задачу можна привести до задачі лінійного програмування й скористатися для її розв’язання симплекс-методом.
2. Приведення задачі дробово-лінійного програмування до задачі лінійного програмування.
Позначимо знаменник цільової функції через 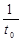 . Природно, тут передбачається, що в області допустимих розв’язків
. Природно, тут передбачається, що в області допустимих розв’язків 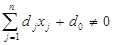 . Це означає, що скрізь в області допустимих розв’язків знаменник не змінює знак. Тому, не обмежуючи області застосування, припустимо, що
. Це означає, що скрізь в області допустимих розв’язків знаменник не змінює знак. Тому, не обмежуючи області застосування, припустимо, що 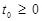 , тобто знаменник додатній. Якщо виявиться, що знаменник від’ємний, то, помноживши чисельник і знаменник на (-1), знову одержимо
, тобто знаменник додатній. Якщо виявиться, що знаменник від’ємний, то, помноживши чисельник і знаменник на (-1), знову одержимо 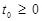 .
.
Таке позначення знаменника означає, що у задачі зявиться нове обмеження
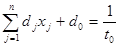 , (4)
, (4)
або
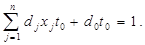 (5)
(5)
Цільова функція тепер має вид
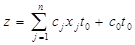 (6)
(6)
Всі обмеження (1) помножимо на 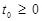 та одержимо
та одержимо
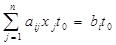 (7)
(7)
Введемо нові змінні
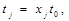 (8)
(8)
які будуть мати той жен знак, що й xj, тому що 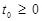 . Тоді в нових змінних задача (1)-(3) записується у виді:
. Тоді в нових змінних задача (1)-(3) записується у виді:
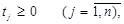 (9)
(9)
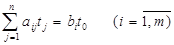 , (10)
, (10)
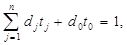 (11)
(11)
 (12)
(12)
Нагадоємо, що (11) – це нове обмеження, що з’явилося внаслідок підстановки.
У нових змінних tj задача (9)-(12) уже є задачею лінійного програмування. Звернемо увагу на те, що хоча в початковому вигляді (1) задача записана в канонічному вигляді, це ніяк не обмежує області застосування підстановки, а просто означає, що перед підстановкою (4) систему треба приготувати до розв’язання, тобто вести додаткові змінні й, якщо потрібно, штучні, як того вимагає стандартна схема застосування симплексного методу.
3. Розв’янання задач дробово-лінійного програмування.
Розв’янання задачі дробово-лінійного програмування проілюструємо на конкретному прикладі.
Для виробництва двох виробів А і В підприємство використовує три типи технологічного обладнання. Кожний з виробів повинен пройти обробку на даному типі обладнання. Час обробки кожного з виробів, витрати, пов’язані з виробництвом одного виробу, наведено у таблиці. Обладнання 1-го та 3-го типів підприємство може використовувати не менше 48 і 6 годин відповідно, а обладнання 2-го типу не більше 50 годин.
| Тип обладнання | Витрати часу на обробку одного виробу, год. | |
| А | В | |
| Витрати на виробництво одного виробу, тис. грн.. |
Визначити обсяг виробництва продукції за умови найменшої середньої собівартості одного виробу.
4. Графічне розв’язання задачі дробово-лінійного програмування.
У загальному випадку цільова функція задачі дробово-лінійного програмування має вигляд
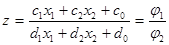 (13)
(13)
З огляду на те, що 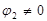 , тобто
, тобто 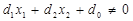 , можна записати
, можна записати
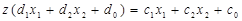 (14)
(14)
З рівняння (13) виразимо змінну х2 через х1
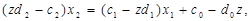 (15)
(15)
або
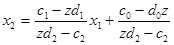 (16)
(16)
Останнє рівняння можна розглядати як рівняння прямої 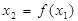 з кутовим коефіцієнтом
з кутовим коефіцієнтом 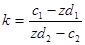 . З виду k можна зробити висновок, що при зміні значення цільвої функції z, змінюється k- кут нахилу лінії рівня. На відміну від задачі ЛП, щоб досягти оптимального значення z, лінію рівня потрібно повертати, а не переміщувати паралельно самій собі. Залишилося з’ясувати два питання:
. З виду k можна зробити висновок, що при зміні значення цільвої функції z, змінюється k- кут нахилу лінії рівня. На відміну від задачі ЛП, щоб досягти оптимального значення z, лінію рівня потрібно повертати, а не переміщувати паралельно самій собі. Залишилося з’ясувати два питання:
· як повертати: за годинковою стрілкою або проти годинкової стрілки;
· навколо якої точки здійснювати поворот.
Звернемо увагу на те, що
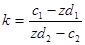 . (17)
. (17)
Кутовий коефіцієнт є функцією z. Щоб визначити, як повертати лінію рівня для досягнення zmax або zmin, необхідно дослідити функцію k(z) на монотонність.
Обчислемо похідну
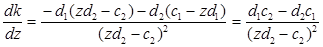 (18)
(18)
· якщо 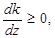 то k зростає при збільшенні z;
то k зростає при збільшенні z;
· якщо 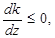 то k спадає при збільшенні z..
то k спадає при збільшенні z..
Таким чином, якщо
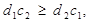 (19)
(19)
то 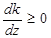 й при збільшенні z лінія рівня повертається проти годинникової стрілки.
й при збільшенні z лінія рівня повертається проти годинникової стрілки.
Якщо
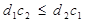 (20)
(20)
то 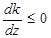 й збільшенні z лінія рівня повертається за годинниковою стрілкою.
й збільшенні z лінія рівня повертається за годинниковою стрілкою.
З рівняння (15) випливає, що при 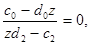 тобто при
тобто при 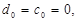 лінія рівня проходить через початок координат і, отже, поворот здійснюється навколо початку координат.
лінія рівня проходить через початок координат і, отже, поворот здійснюється навколо початку координат.
Якщо, 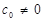 й/або
й/або 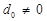 , то рівняння (15) визначає пучок прямих, які проходять через деяку точку
, то рівняння (15) визначає пучок прямих, які проходять через деяку точку 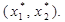 Рівняння пучка прямих, які проходять через задану точку
Рівняння пучка прямих, які проходять через задану точку 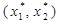 з урахуванням (15), запишеться у вигляді:
з урахуванням (15), запишеться у вигляді:
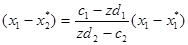 (21)
(21)
Так як з (15) маємо
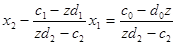 (22)
(22)
То підставивши (21) в (20), одержимо
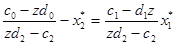 (23)
(23)
звідки
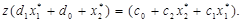 (24)
(24)
Останнє рівняння повинне виконуватися для всіх значень z. Це можливо, тільки якщо
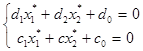 (25)
(25)
Таким чином, у випадку якщо 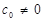 й/або
й/або 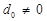 , поворот лінії рівня здійснюється навколо точки з координатами
, поворот лінії рівня здійснюється навколо точки з координатами 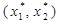 , які є розв’язком системи (25).
, які є розв’язком системи (25).
Установивши напрям повороту, знаходимо вершину або вершини багатокутника розв’язків, у яких функція приймає екстремальне значення, або встановлюємол необмеженість значення цільової функції задачі.
Питання для самоконтролю.
· Сформулюйте задачу дробово-лінійного програмування.
· Дайте економічну інтерпретацію задачі дробово-лінійного програмування.
· Сформулюйте алгоритм розв’язання задачі дробово-лінійного програмування.
· У чому принципова відмінність геометричної інтерпретації задачі дробово-лінійного програмування?
· Навколо якої точки здійснюється поворот лінії рівня?
· Сформулюйте алгоритм розв’язання задачі дробово-лінійного програмування графічним методом.
Тема 7. Нелінійні оптимізаційні моделі економічних систем.
Лекція 15.
Тема лекції: Задачі нелінійного програмування
Мета: ознайомити студентів з методами розв’язання задач нелінійного програмування.
План лекції
1. Класичні методи розв’язування задач нелінійного програмування.
2. Метод множників Лагранжа.
3. Задачі опуклого прогрмування.
Література:
1. Лавріненко Н.М., Латинін С.М., Фортуна В.В., Безкровний О.І. Основи економіко-метематичного моделювання: Навч. Посіб. - Львів: «Магнолія 2006», 2010.- 540с.
2. Іванюта І. Д. Практикум з математичного програмування: Навчальний посібник / І. Д. Іванюта, В. І. Рибалка, І. А. Рудоміно-Дусятська. – К.: «Слово», 2008. - 296 с.
3. Кучма М. І. Математичне програмування: приклади і задачі: Навчальний посібник / М.І. Кучма. – Львів: «Новий Світ - 2000», 2006. - 344 с.
4. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1993. – 336 с.
1. Класичні методи розв’язання задач нелінійного програмування.
Загальна задача нелінійного програмування полягає у знаходженні максимального(мінімального) значення функції
Z=f(x1, x2,….. xn) →max/ min (1)
за умов
gi(x1, x2,….. xn) { ≤=≥}bi, i=1,2…..m (2)
де всі функції (або їх частина) нелінійні.
Функція f з (1) – цільова функція, а умови gi з (2) - умовами обмеження.
Сукупність змінних, що задовольняють обмеженням (2) задачі називається допустимим розв’язком або планом. Кожному допустимому розв ’ язкувідповідає певне значення цільової функції.
Допустимий розв ’ язок (план), при якому цільова функція набуває найбільшого (найменшого) значення називається оптимальним планом. Найбільше (найменше) значення функції в допустимій області розв’язків називається глобальним максимумом (мінімумом). Задачі НП розв’язуються значно складніше, ніж задачі ЛП. Для відшукання їх розв’язків немає універсального методу.
Лише для небагатьох типів задач НП розроблені обчислювальні методи їх розв’язання.
Найбільш вивчені задачі з нелінійною цільовою функцією певного виду і лінійними обмеженнями. Для розв’язання таких задач використовується ідея зведення до лінійного вигляду, що допускає застосування симплексного методу. Ще однією особливістю задач НП є наявність точок оптимуму, які можуть бути як граничними, так і внутрішніми точками області допустимих розв’язків.
Як згадувалось вище, найбільш вивченими є задачі з нелінійною цільовою функцією і лінійними обмеженнями, які можна класифікувати таким чином:
- Задачі дробово-лінійного програмування
Z=(∑cixi)/(∑dixi) →max/ min
за умов
∑aijxj =bi, (i=1,2…..m)
xj ≥0 (j=1,2…..n)
- Сеперабельна задача НП
f(x1, x2,….. xn) =∑fi(xi) →max/ min
за умов
∑aijxj{ ≤=≥}bi, (i=1,2…..m)
xj ≥0 (j=1,2…..n)
- Квадратична задача НП
f(x1, x2,….. xn) =∑cjxj +∑∑djixixj →max/ min
за умов
∑aijxj{ ≤=≥}bi, (i=1,2…..m)
xj ≥0 (j=1,2…..n)
- Задача опуклого програмування
Це задача, в якій цільова функція f і функції обмежень gi є опуклими (вгнутими) функціями. Суттєвим для цих задач є вимога гладкості, тобто функції f і gi повинні бути неперервними та диференційованими і мати неперервні частинні похідні хоча б до другого порядку включно.
Розглянемо задачу (5), якщо на змінні не накладаються умови обмежень.
Така задача вирішується класичними методами дифереціального числення.
Нехай Z=f(x1, x2,….. xn) неприривно – диференційована функція в своїй області визначення. Необхідною умовою екстремуму в точці Х0 функції Z=f(x1, x2,….. xn) є рівність нулю градієнта функції 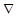 Z(X0)=0.Для функції Z=f(x1, x2,….. xn) запишемо матрицю Гессе:
Z(X0)=0.Для функції Z=f(x1, x2,….. xn) запишемо матрицю Гессе:
Н= 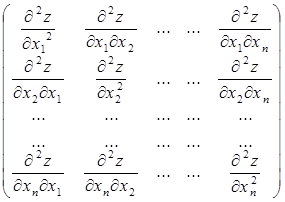
яка складається з частинних похідних другого порядку.
Головні мінори матриці Гессе позначимо:
M1= 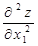 , M2=
, M2=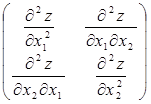 , ………….,Mn=H,
, ………….,Mn=H,
де fij=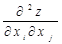 – значення частинної похідної другого порядку функції Z в точці X0.
– значення частинної похідної другого порядку функції Z в точці X0.
Якщо всі головні мінори M1, M2, M3, …… Mn>0, то Х0 – точка локального мінімуму. Якщо головні мінори почергово міняють знак, починаючи з мінуса, то точка Х0 – точка локального максимуму. Проаналізувавши всю область допустимих розв’язків, можна виділити серед локальних екстремумів найбільший і найменший, які і будуть глобальними.
2. Метод множників Лагранжа.
Розглянемо задачу НП з обмеженнями – рівностями:
Z=f(x1, x2,….. xn) →max/ min (3)
за умов
gi(x1, x2,….. xn)=bi, i=1,2…..m (4)
в якій f і gi двічі неперервно диференційовані функції.
Для визначення оптимальних точок цієї задачі, введемо набір змінних λi (i=1,2,….m), які називаються множниками Лагранжа, і побудуємо функцію Лагранжа
L(x1, x2,….. xn, λ1,, λ2,...., λm)= f(x1, x2,….. xn) + ∑ λi(bi - gi(x1, x2,….. xn)) (5)
Відшукання умовного екстремуму задачі зводиться до знаходження безумовного екстремуму функції Лагранжа (5). Характер оптимальності з’ясовується аналогічно, як і у випадку безумовного екстремуму.
|
|
 2014-02-04
2014-02-04 838
838








