Постановка задач параметричного програмування

Транспортна задача.

Транспортна задача одна з найпоширеніших задач лінійного програмування. Її мета – розробка найбільш раціональних шляхів і способів транспортування однорідної продукції від постачальників до споживачів.

У загальному вигляді транспортну задачу можна сформулювати так: в m пунктах постачання А₁,А₂,…… A_m (надалі постачальники) міститься однорідна продукція у кількості відповідно а₁, а₂,….. а_m. Цю продукцію потрібно перевезти в n пункти призначення B₁,B₂,…… B_n (надалі споживачі) у кількості відповідно b₁, b₂,….. b_n. Вартість перевезення одиниці товару (тариф) із пункту А_i в пункт B_j дорівнює с_ji.

Математична модель транспортної задачі має такий вигляд:

F(x_ji)= ∑∑ x_ji с_ji→ min (4)

за умов

∑x_ji =a_i (i=1,2…..m) (5)

∑x_ji =b_j (j=1,2…..n) (6)

x_ji≥0 (i=1,2…..m; j=1,2…..n) (7)

Алгоритм і методи розв’язання транспортної задачі можна використати для знаходження розв’язку деяких економічних задач, які не мають нічого спільного з транспортуванням вантажів. У цьому разі величини тарифів перевезення с_ji мають різний зміст залежно від конкретної задачі. До таких задач належать наступні:

· Оптимальне закріплення за верстатами операцій з обробки деталей. У них с_ji означає продуктивність праці.

· Розміщення сільськогосподарських культур за ділянками землі різної врожайності.

· Оптимальні призначення або проблема вибору.

· Задача про скорочення виробництва із врахуванням загальних витрат на виготовлення і транспортування продукції

· Збільшення продуктивності автомобільного транспорту за рахунок мінімізації порожнього пробігу

Основні теореми транспортної задачі.

Означення 1. Якщо у транспортної задачі виконується умова балансу

∑b_j = ∑a_i (8)

То задача називається закритою або збалансованою.

Означення 2. Планом транспортної задачі називається сукупність величин x_ji (i=1,2…..m; j=1,2…..n), який задовольняє умови обмеження (5) – (7).

Означення 3. Опорний план транспортної задачі називається не виродженим, якщо він містить N=m+n-1 додатних елементів x_ji

Означення 4. Якщо опорний план містить менше N<m+n-1 додатних елементів, то він називається виродженим.

Означення 5. Оптимальним планом транспортної задачі називають матрицю Х^*, яка задовольняє умови задачі (5) – (7) і для якої цільова функція F набуває мінімального значення.

Теорема 1. (Необхідна і достатня умова існування розв’язку задачі ТЗ).

Транспортна задача має розв’язок тоді і тільки тоді, коли вона збалансована, тобто виконується умова (8).

Теорема 2. Для того щоб деякий план Х транспортної задачі був оптимальним необхідно і достатньо, щоб йому відповідала така система із m+n чисел u_i (i=1,2…..m) v_j (j=1,2…..n) для якої виконуються умови

v_j - u_i = с_ji для x_ji>0

v_j - u_i ≤ с_ji для x_ji=0.

Означення 6. Числа v_j та u_i називаються потенціалами строк та стовпців.

Метод північно-західного кута (діагональний.)

Побудова опорного плану задачі починають із заповнення верхньої клітинки таблиці x₁₁, в яку записують менше з двох чисел a₁ та b₁.

Далі переходять до наступної клітинки в рядку або стовпчику і заповнюють ії і т.д. Закінчують заповнювати таблицю у правій нижній клітинці.

Зауважемо, що користуючись методом північно-західного кута початковий опорний план залежить від величин a_i та b_j і зовсім не залежить від вартостей перевезення с_ji, а тому він буде далекий від оптимального.

Метод найменшої вартості.

Сутність цього методу полягає у тому, що на кожному кроці заповнюють клітинки таблиці, яка має найменшу вартість перевезеня одиниці продукції між постачальниками та споживачами.

Метод потенціалів.

Після перевірки транспортної задачі на сбалансованість та визначення початкового плану транспортної задачі приступаємо до розрахунку потенціалів строк і стовпців для заповнених кліток:

v_j - u_i = с_ji для x_ji>0 (9)

Оскільки заповнених клітинок є m+n-1, то система рівнянь (9) із m+n невідомих містить m+n-1 рівнянь. Прийнявши одне невідоме за нуль, наприклад, u₁=0, решту знаходимо.

Для побудованого опрного плану і знайдених потенціалів обчислюємо оцінки вільних клітинок:

Δ_ji =v_j - u_i - с_ji

Якщо, Δ_ji ≤0, то побудований опрний план є оптимальним.

Якщо, хоча б для однієї клітинки ця умова не виконується, то опорний план не є оптимальним і треба від нього переходити до нового опорного плану.

Перехід від одного опорного плану до іншого здійснюється заповненням клітинки, для якої порушено умови оптимальності. Якщо таких клітинрк кілька, то для заповнення вибіраютьтаку, що має найбільшє порушенняі з неї будують цикл перерозподілу.

Означення 7. Циклом у транспортної задачі називають замкнену ламану лінію, вершини якої розміщуються в заповнених клітинках таблиці, а сторонни проходять уздовж рядків і стовпчиків таблиці.

Для вибраної вільної клітинки і клітинок, що пов’язані з нею циклом, здійснюють перерозподіл продукції в межах цього циклу за такими правилами:

· Кожній вершині циклу приписують певний знак, причому вільній клітинці – знак «+», а всім іншим по черзі- знаки «-» та «+»;

· У поржню клітинку переносять менше з чисел x_ji, що стоять у клітинках зі знком «-». Одночасно це число додають до відповідних чисел, які розміщені в клітинках зі знаком «+».

Приклад. Розв’язати транспортну задачу.

						ui
vj

Питання для самоконтролю.

· Сформулюйте задачу ЛП в загальній формі.

· Сформулюйте задачу ЛП в канонічній формі.

· Сформулюйте задачу ЛП в стандартній формі.

· Запишіть задачу ЛП в матричній формі.

· Запишіть задачу ЛП в векторній формі.

· Дайте означення опорного плану задачі ЛП.

· Дайте означення опуклої множини.

· Дайте означення кутової точки.

· Дайте означення допустимого плану.

· Дайте означення оптимального плану.

· Що таке вектор нормалі цільової функції?

· Дайте означення лінії рівня цільової функції.

· В чому полягає симплекс-метод із стандартним базисом?

· Коли використовують симплекс-метод зі штучним базисом?

· Принципи заповнення симплекс-таблиці.

· Що таке розв’язувальний елемент симплекс-таблиці?

· Як перевірити опорний план на оптимальність?

· Поясніть метод Жордана-Гауса.

· Що таке штучні змінні?

· Чому транспортну задачу вирішують іншими методами, якщо це задача лінійного програмування?

· Яка транспортна задача називається закритою?

· Що робити якщо транспортна задача відкрита?

· Дайте означення опорного плану транспортної задачі.

· Коли опорний план транспортної задачі не вироджений?

· Що робити, якщо опорний план транспортної задачі вироджений?

· Дайте означення оптимального опорного плану транспортної задачі.

· Сформулюйте необхідні і достатні умови існування розв’язку транспортної задачі.

· Як построїти потенціали строк і стовпців?

· В чому полягає метод північно-західного кута?

· В чому полягає метод найменших витрат?

· Як визначити, що опорний план оптимальний?

· Дайте означення циклу перерозподілу поставок.

Тема 5. Цілочислові та параметричні задачі лінійного програмування

Тема 6. Елементи теорії ігор

Тема 7. Нелінійні оптимізаційні моделі економічних систем

Лекція 2.

Тема лекції: Задачі нелінійного програмування

Мета: ознайомити студентів з методами розв’язання задач цілочислового програмування методом Гоморі та з основними методами розв’язування задач нелінійного програмування, розв’язання задач теорії ігор та ознайомлення з методами оцінювання ризиків.

План лекції

1. Постановка задач цілочислового програмування.

2. Постановка задач параметричного програмування.

3. Класичні методи розв’язування задач нелінійного програмування.

Література:

1. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1993. – 336 с.

2. Іванюта І.Д. Практикум з математичного програмування: Навчальний посібник/ І.Д. Іванюта, В.І. Рибалка, І.А. Рудоміра – Дусятська. – К.: «Слово», 2008. – 296 с.

3. Кучма М.І. Математичне програмування: приклади і задачі: Навчальний посібник/ М.І. Кучма. - Львів: «Новий Світ - 2000», 2006. – 344 с.

4. А. Черемис, Р. Юринець, О. Мищишин. Методи оптимізації в економіці. Навчальний посібник. – К.: Центр навчальної літератури, 2006. – 152 с.

1. Постановка задач цілочислового програмування.

Задача цілочислового програмування формулюється так:

Z= 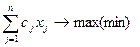(1)

за умов

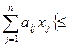,=b_i, i=, (2)

x_j≥0, (j=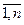), (3)

x_j - цілі, (j=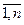), (4)

умова цілочисельності (4), яка додається до звичайної задачі ЛП, суттєво ускладнює її розв’язання.

Метод Гоморі. Сутність методу Гоморі (метод відтинання) полягає у тому, що спочатку розв’язується звичайна задача ЛП без урахування вимог цілочисельності змінних. Якщо отриманий оптимальний план задачі цілочисловий, то задача розв’язана. У протилежному випадку у модель вводиться спеціальне додаткове обмеження, що враховує цілочисельність змінних і володіє такими властивостями;

- вона повинна бути лінійною;

- вона повинна відтинати знайдений оптимальний нецілочисловий план задачі;

- не повинна відтинати ні одного цілочислового плану.

Додаткове обмеження, що має перелічені вище властивості, називається правильним відтинанням.

Це додаткове обмеження вводиться до оптимального плану якщо серед компонент оптимального розв’язку яка має найбільшу дробову частину. На базі цієї змінної будується додаткове обмеження Р.Гоморі:

де 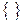- дробова частина числа,

=а-[a].

Параметричне програмування являє собою один з розділів математичного програмування, вивчає завдання, в яких цільова функція або обмеження залежать від одного або кількох параметрів.
Необхідність розгляду подібних завдань обумовлена різними причинами. Однією з основних є та, що вихідні дані для чисельного рішення будь-якої реальної задачі оптимізації в більшості випадків визначаються наближено або може змінюватися під впливом якихось чинників, що може істотно позначитися на оптимальності вибираної програми (плану) дій. Відповідно, розумно вказувати не конкретні дані, а діапазон можливої зміни даних, що б в результаті рішення мати найкращі плани для будь-якого варіанту вихідних даних.
З математичної точки зору параметричне програмування виступає як один із засобів аналізу чутливості рішення до варіації вихідних даних, оцінки стійкості рішення.

Зауважимо, що існують різні підходи до подібного аналізу (наприклад, на основі постановки двоїстої задачі). Тут ми, не посилаючись на двоїсті оцінки, розглянемо найпростіші варіанти рішення для самих найпростіших параметричних задач.
Розглянемо задачу параметричного лінійного програмування, в якій тільки коефіцієнти цільової функції лінійно залежать від деякого єдиного параметра λ (часу, температури і т. п.):
Відшукати максимум (або мінімум) функції:

за умов

Якщо звернутися до геометричної інтерпретації задачі, то можна помітити, що вектор-градієнт лінійної форми визначається її параметром. Наприклад, для цільової функції L (х, λ) = λх₁ + (1-λ) х₂ при різних значеннях параметра λ градієнт визначає різні напрямки зростання функції.
Неважко бачити, що, якщо при деякому значенні параметра максимум досягається в вершині A, то невелика варіація цього значення дещо змінить напрямок градієнта, але не змінить положення точки максимуму. Звідси напрошується висновок, що деякий план, оптимальний при λ = λ₀ оптимальний і в околиці λ₀, тобто при α ≤ λ ≤ β де λ₀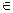[α, β].
Можна помітити, що при градієнті, що став перпендикулярним деякої сторони багатокутника планів, маємо два різних оптимальних опорних плани з одним і тим же значенням лінійної форми, звідки можна стверджувати безперервність екстремуму лінійної форми за λ.

У разі необмеженість безлічі планів можна стверджувати, що якщо лінійна форма не обмежена при λ = λ₀, то вона не обмежена при всіх λ, більших або менших λ₀.
Алгоритм для вирішення завдань параметричного лінійного програмування в разі залежності від параметра коефіцієнтів цільової функції незначно відрізняється від звичайного симплексного методу.
У разі залежності від параметра компонент вектора правих частин обмежень, тобто рішення задачі пошуку екстремуму функції

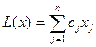
за умов

Приклад 2.

за умов

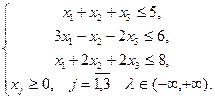
Приклад 3.

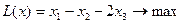
за умов

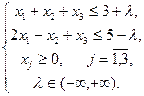
Для того щоб вирішити задачу, достатньо вирішити двоїсту задачу до неї, яка має вигляд

за умов

3. Класичні методи розв’язання задач нелінійного програмування.

Загальна задача нелінійного програмування полягає у знаходженні максимального(мінімального) значення функції

Z=f(x₁, x₂,….. x_n) →max/ min (5)

за умов

g_i(x₁, x₂,….. x_n) { ≤=≥}b_i, i=1,2…..m (6)

де всі функції (або їх частина) нелінійні.

Функція f з (5) – цільова функція, а умови g_i з (6) - умовами обмеження.

Сукупність змінних, що задовольняють обмеженням (6) задачі називається допустимим розв’язком або планом. Кожному допустимому розв ’ язкувідповідає певне значення цільової функції.

Допустимий розв ’ язок (план), при якому цільова функція набуває найбільшого (найменшого) значення називається оптимальним планом. Найбільше (найменше) значення функції в допустимій області розв’язків називається глобальним максимумом (мінімумом). Задачі НП розв’язуються значно складніше, ніж задачі ЛП. Для відшукання їх розв’язків немає універсального методу.

Лише для небагатьох типів задач НП розроблені обчислювальні методи їх розв’язання.

Найбільш вивчені задачі з нелінійною цільовою функцією певного виду і лінійними обмеженнями. Для розв’язання таких задач використовується ідея зведення до лінійного вигляду, що допускає застосування симплексного методу. Ще однією особливістю задач НП є наявність точок оптимуму, які можуть бути як граничними, так і внутрішніми точками області допустимих розв’язків.

Як згадувалось вище, найбільш вивченими є задачі з нелінійною цільовою функцією і лінійними обмеженнями, які можна класифікувати таким чином:

- Задачі дробово-лінійного програмування

Z=(∑c_ix_i)/(∑d_ix_i) →max/ min

за умов

∑a_ijx_j =b_i, (i=1,2…..m)

x_j ≥0 (j=1,2…..n)

- Сепарабельна задача НП

f(x₁, x₂,….. x_n) =∑f_i(x_i) →max/ min

за умов

∑a_ijx_j{ ≤=≥}b_i, (i=1,2…..m)

x_j ≥0 (j=1,2…..n)

- Квадратична задача НП

f(x₁, x₂,….. x_n) =∑c_jx_j +∑∑d_jix_ix_j →max/ min

за умов

∑a_ijx_j{ ≤=≥}b_i, (i=1,2…..m)

x_j ≥0 (j=1,2…..n)

- Задача опуклого програмування

Це задача, в якій цільова функція f і функції обмежень g_i є опуклими (вгнутими) функціями. Суттєвим для цих задач є вимога гладкості, тобто функції f і g_i повинні бути неперервними та диференційованими і мати неперервні частинні похідні хоча б до другого порядку включно.

Розглянемо задачу (5), якщо на змінні не накладаються умови обмежень.

Така задача вирішується класичними методами дифереціального числення.

Нехай Z=f(x₁, x₂,….. x_n) неприривно – диференційована функція в своїй області визначення. Необхідною умовою екстремуму в точці Х₀ функції Z=f(x₁, x₂,….. x_n) є рівність нулю градієнта функції 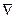Z(X₀)=0.Для функції Z=f(x₁, x₂,….. x_n) запишемо матрицю Гессе:

Н=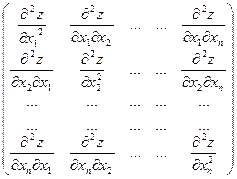

яка складається з частинних похідних другого порядку.

Головні мінори матриці Гессе позначимо:

M₁= _‌‌, M₂=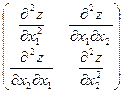, ………….,M_n=H,

де f_ij=– значення частинної похідної другого порядку функції Z в точці X₀.

Якщо всі головні мінори M₁, M₂, M₃, …… M_n>0, то Х₀ – точка локального мінімуму. Якщо головні мінори почергово міняють знак, починаючи з мінуса, то точка Х₀ – точка локального максимуму. Проаналізувавши всю область допустимих розв’язків, можна виділити серед локальних екстремумів найбільший і найменший, які і будуть глобальними.

Метод множників Лагранжа.

Розглянемо задачу НП з обмеженнями – рівностями:

Z=f(x₁, x₂,….. x_n) →max/ min (7)

за умов

g_i(x₁, x₂,….. x_n)=b_i, i=1,2…..m (8)

в якій f і g_i двічі неперервно диференційовані функції.

Для визначення оптимальних точок цієї задачі, введемо набір змінних λ_i (i=1,2,….m), які називаються множниками Лагранжа, і побудуємо функцію Лагранжа

L(x₁, x₂,….. x_n, λ₁,, λ₂,...., λ_m)= f(x₁, x₂,….. x_n) + ∑ λ_i(b_i - g_i(x₁, x₂,….. x_n)) (9)

Відшукання умовного екстремуму задачі зводиться до знаходження безумовного екстремуму функції Лагранжа (12). Характер оптимальності з’ясовується аналогічно, як і у випадку безумовного екстремуму.

Задачі опуклого програмування.

Означення 1. Функція f(x₁, x₂,….. x_n), що задана на опуклій множені Х, називається опуклою, якщо для будь – яких двох крапок Х₁,Х₂ є Х і довільного µє[0;1] виконується співвідношення:

f(µX₁+(1-µ) X₂) ≤ µ f(X₁) +(1-µ) f(X₂)

Означення 2. Функція f(x₁, x₂,….. x_n), що задана на опуклій множині Х, називається вгнутою, якщо для будь яких двох крапок Х₁,Х₂ є Х і довільного µє[0;1] виконується співвідношення

f(µX₁+(1-µ) X₂) ≥ µ f(X₁) +(1-µ) f(X₂).

Якщо f(x₁, x₂,….. x_n) – опукла, то - f(x₁, x₂,….. x_n) – вгнута.

Загальна постановка задачі опуклого програмування:

Z=f(x₁, x₂,….. x_n) →max (10)

за умов

g_i(x₁, x₂,….. x_n) ≤b_i, i=1,2…..m (11)

x_j ≥0 j=1,2,…..n (12)

де f – вгнута і g_i - опуклі функції

Надалі припустимо, що ОДР задачі (10) – (12) не порожня й обмежена.

Теорема 3. Довільний локальний максимум (мінімум) задачі опуклого програмування є глобальним максимумом (мінімумом).

Означення 3. Говорять, що множина ОДР задовольняє умову регулярності, якщо існує хоча б одна крапка

Означення 4. Говорять, що множина допустимих планів (10) – (12) задовольняє умові регулярності, якщо існує хоча б одна крапка х _i з області допустимих розв’язків така, що g_i(x_i)<b_i (i=1,2,….m).

Означення 5. Крапка (Х^*,Λ^*) називається сідловою крапкою функції Лагранжа, якщо L(Х,Λ^*) ≤L(Х^*,Λ^*)≤L(Х^*,Λ) для всіх x_j ≥0 (j=1,2,…n) і λ_i≥0 (i=1,2,….m).

Теорема 4. (Куна-Такера). Нехай для ОДР задачі опуклого програмування (10) – (12) виконується умова регулярності. План Х^*буде оптимальним планом цієї задачі тоді і тільки тоді, коли існує такий вектор Λ^*, λ_i≥0 (i=1,2,….m), що пара (Х^*,Λ^*) – сідлова крапка функції Лагранжа.

Зазначимо, що умови Куна-Такера мало придатні для знаходження оптимального розв’язку, вони лише характеризують розв’язок, тобто дають можливість перевірити деякий розв’язок на оптимальність.

1. Задачі опуклого програмування.

Розглянемо задачу квадратичного програмування, яка є окремим випадком задач опуклого програмування.

Означення 6. Квадратичною формою відносно змінних x₁, x₂,….. x_n називається функція Z, яка має вигляд Z=∑∑с_jix_ix_j.

Означення 7. Квадратична форма Z називається додатньо (від’ємно) – визначеною, якщо Z(Х)>0 (Z(Х)<0) для всіх значень змінних Х, окрім крапки Х=(0,0,……0).

Означення 8. Квадратична форма Z називається додатньо (від’ємно) – напіввизначеною, якщо Z(Х) ≥0 (Z(Х) ≤0) для будь якого набору значень змінних Х =(x₁, x₂,….. x_n) і, крім того, існує такий набір змінних Х^*, де не всі змінні одночасно рівні нулю, що Z(Х) =0.

Теорема 5. Квадратична форма є опуклою функцією, якщо вона додатньо-напіввизначена.

Постановка задачі квадратичного програмування має вигляд:

Z=∑∑с_jix_ix_j.+ ∑d_jx_j→max/ min (13)

за умов

∑a_ijx_j ≤b_i, (i=1,2…..m),

x_j ≥0 (j=1,2…..n),

де ∑∑с_jix_ix_j - від’ємно (додатньо) – напіввизначена квадратична форма.

Алгоритм знаходження розв’язку задачі квадратичного програмування.

1. Складаємо функцію Лагранжа.

2. Записуємо необхідні і достатні умови існування сідловок точки для функції Лагранжа.

3. Використовуючи метод штучного базису, встановлюємо відсутність сідловок крапки для функції Лагранжа, або знаходимо ії координати.

4. Записуємо оптимальний план початкової задачі й обчислюємо значення цільової функції.

Питання для самоконтролю.

· Сформулюйте задачу цілочисельного програмування.

· Напішить рівняння Гоморі.

· Сформулюйте загальну задачу НП.

· Сформулюйте задачу сепарабельного програмування.

· Сформулюйте задачу квадратичного програмування.

· Сформулюйте задачу опуклого програмування.

· Поясніть метод множників Лагранжа.

· Сформулюйте означення сідловок точки функції Лагранжа.

· Сформулюйте теорему Куна-Такера.

· Сформулюйте означення додатньо-визначеної квадратичної форми.

· Сформулюйте означення додатньо-напіввизначеної квадратичної форми.

· Сформулюйте параметричну задачу, параметр якої присутній у функції цілі.

· Сформулюйте параметричну задачу, параметр якої присутній у системі обмежень.

· Вкажіть на взаємозв’язок параметричної задачі та стійкості рішень задачі ЛП.

· Вкажіть взаємозв’язок параметричної задачі на чутливість рішень задачі ЛП.

Тема 5. Цілочислові та параметричні задачі лінійного програмування

Тема 6. Елементи теорії ігор

Тема 7. Нелінійні оптимізаційні моделі економічних систем

Лекція 3.

Тема лекції: Матричні ігри

Мета: ознайомити студентів з методами розв’язання задач теоріі ігор та зведення їх до задач ЛП.

План лекції

1. Постановка задач теорії ігор з нульовою сумою.

2. Задачі з сідловою точкою. Задачі в чистих стратегіях.

3. Ігри в мішаних стратегіях.

4. Зведення задач теорії ігор до задач ЛП.

Література:

1. Лавріненко Н.М., Латинін С.М., Фортуна В.В., Безкровний О.І. Основи економіко-метематичного моделювання: Навч. Посіб. - Львів: «Магнолія 2006», 2010.- 540с.

2. Іванюта І. Д. Практикум з математичного програмування: Навчальний посібник / І. Д. Іванюта, В. І. Рибалка, І. А. Рудоміно-Дусятська. – К.: «Слово», 2008. - 296 с.

3.Кучма М. І. Математичне програмування: приклади і задачі: Навчальний посібник / М.І. Кучма. – Львів: «Новий Світ - 2000», 2006. - 344 с.

1. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1993. – 336 с.

1. Постановка задач теорії ігор з нульовою сумою.

На практиці дуже часто виникають ситуації, коли необхідно приймати рішення в умовах невизначеності, тобто в умовах, коли дві або більш сторін мають на меті різні цілі, но результат для кожної із сторін залежить від дій супротивника. Наприклад, гра в шахи, шашки і т.д. В економіці конфліктні ситуації зустрічаються дуже часто: продавець і покупець, банк і клієнт, постачальник і споживач.

В 1944 році з’явилася математична дисципліна – теорія ігор, основою для якої стала монографія американського економіста Неймана.

Теорія ігор – це теорія математичної моделі конфліктних ситуацій, інтереси гравців котрих різні і кожний з них досягає своєї цілі (мети) різними шляхами.

Результат гри є виграшем для одних і програшем для других.

Означення 1. Модель любої конфліктної ситуації зветься грою.

Означення 2. В процесі гри кожний гравець висуває власну стратегію. Стратегія гравця – сукупність правил, по котрих при кожному ході відбувається вибір певних дій. Цей вибір залежить від сформованих обставин.

Означення 3. гра зветься парною, якщо в ній беруть участь дві сторони.

Означення 4. Кількісна оцінка результатів гри зветься платою.

Означення 5. Парна гра зветься грою з нульовою сумою, якщо програш одного є виграшем іншого.

Означення 6. Стратегія гравця називається оптимальною, якщо при повторенні гри вона забезпечує гравцю максимально можливий середній виграш (або теж само- мінімально можливий середній програш).

1. Задачі з сідловою точкою. Задачі в чистих стратегіях.

Розглянемо парну гру:

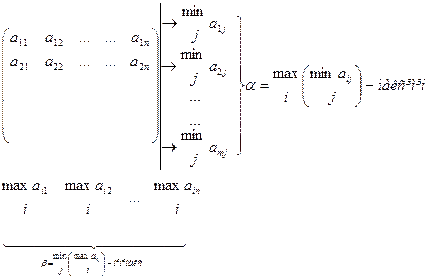
Приклад 1. Задана платіжна матриця А парної гри з нульовою сумою: А=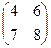. Знайти ціну гри, сідлову точку гри.

Приклад 2..Задана платіжна матриця А парної гри з нульовою сумою: А=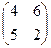. Знайти верхнью та нижню ціну гри.

2. Ігри в мішаних стратегіях. Основна теорема теорії ігор.

Якщо немає сідловок точки, то гра ведеться в мішаних стратегіях, тобто розглядається не вибір можливої стратегії, а ймовірність з котрою обирається ця стратегія. Мішана стратегія визначається сукупністю ймовірностей різних стратегій.

Нехай гравець А для визначення своєї мішаної стратегії використав метод випадкового вибіру.

Нехай х₁ – ймовірність вибору 1-ої стратегії;

х₂ - ймовірність вибору 2-ої стратегії;

…………………………………………………

x_m - ймовірність вибору m-ої стратегії.

Означення 1. Мішаною стратегією гравця А називається упорядкований набір m чисел х₁, х₂, ….., x_m, які задовольняють умовам: 0≤x_i≤1, i=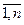 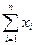=1.

Мішані стратегії гравців А та В позначають 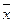=(x₁,x₂, …, x_m), 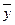=(y₁,y₂,…,y_n).

Всяка матрична гра з нульовою сумою має оптимальне рішення в мішаних стратегіях, при цьому відхилятися гравцям від цих стратегій не вигідно.

Теорема. О методі знаходження рішення.

Для того, щоб число ν було ціною гри, а Х^* та Y^* - оптимальними стратегіями, необхідно та достатньо, щоб виконувались умови:

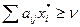j=

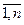
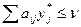i=

Визначення оптимальних стратегій та ціни гри створюють процес знаходження рішення гри.

Теорема 2. Якщо один з гравців використовує мішану оптимальну стратегію, то його виграш дорівнює ціні гри ν незалежно від того, з якими частотами буде використовувати другий гравець стратегії, які вийшли до оптимальної стратегії(в тому числі і чисті стратегії).

Розглянемо гру з платіжною матрицею 2х2: A=.

Якщо сідлової точки нема, рішення гри є мішані стратегії 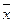=(х₁,х₂) та 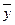=(y₁,y₂) стратегії гравців А та В, для котрих ймовірністі x_i y_i відмінні від нуля, звуться активними.

Стратегію гравця А шукаємо по формулі ХА=, де Х=(х₁,х₂), =(ν, ν).

До даної системи рівнянь додаємо норміровочне рівняння х₁+х₂=1.

Для гравця В:

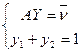
де Y=, =.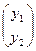

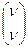Розв’язавши систему рівнянь знайдемо оптимальні стратегії гравців та ціну гри ν.

Наслідок. Для того, щоб х^*, була оптимальною мішаною стратегією матричнох гри з матрицею А та ціною гри ν, необхідно та достатньо, щоб виконувались наступні нерівності:

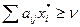j=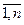

Аналогічно для гравця В: Для того, щоб у^* була оптимальною мішаною стратегією матричної гри з матрицею А та ціною гри ν, необхідно та достатньо, щоб виконувались наступні нерівності:

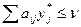i=

Таким чином, для розв’язування гри необхідно визначити стратегії, що задовольняють вишенаведані системи обмежень та умови нормування:

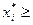0, =1, i=, , 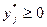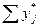=1, j=.

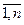Цей наслідок дозволяє сформулювати для розв’язання гри пару задач лінійного програмування.

3. Зведення задач теорії ігор до задач ЛП.

Якщо один з гравців застосовує свою оптимальну стратегію х^*, то інший не може покращити своє становище, тобто для оптимальної стратегії справедливі співвідношення:

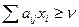j=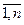, x_i≥0, 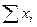=1, i=за умов ν→Мах.

Перетворимо цю задачу, здійснивши підстановку p_i=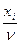, і отримаємо

→Min,тому що ν→Мах.

Таким чином, маємо задачу ЛП, розв’язуючи яку, отримаємо значення p_i, за допомогою яких шляхом оберної підстановки визначимо оптимальні значення ймовірностей, що складають оптимальну мішану стратегію.

А здійснивши підстановку q_j=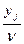і враховуючи, що гравець В прагне мінімізувати програш, отримаємо пару двоїстих задач ЛП, розв’язання яких дозволить визначити оптимальні стратегії гравців А та В:

.

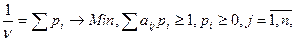
Таким чином, процедура розв’язування гри двох осіб є наступною:

1. Розраховуємо нижню та верхню ціну гри; якщо вони рівні між собою, то гра розв’язана.

2. Спрощуємо гру шляхом виключення домінованих стратегій.

3. Формулюємо пару задач ЛП, розв’язавши одну з яких, встановлюємо оптимальну мішану стратегію одного з гравців (зручніше гравця В).

4. За розв’язком прямої задачі знаходимо розвязок двоїстої задачі.

5. Шляхом оберненої підстановки визначемо оптимальні стратегії для спрощеної гри та доповнюємо їх домінованими чистими стратегіями з ймовірністю використання, що рівні нулю.

Питання для самоконтролю.

· Дайте визначення гри двох осіб з нульовою сумою.

· Дайте визначення сідловок точки.

· Дайте визначення середнього виграшу.

· Що таке чиста стратегія?

· що таке мішана стратегія?

· Що таке домінована стратегія?

· Сформулюйте основну теорему теорії ігор для двох осіб.

· Як звести задачу теорії ігор до задачі ЛП?