Таблиця 1.
| Робітники | Продуктивність праці, грн./год, на обладнанні | |||
Початковий розподіл можна виконувати довільним способом. Оптимальний розподіл призначень має вигляд
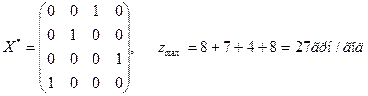 .
.
6. Розподільчи задачі загального типу.
Загальна розподільча задача ЛП – це розподільча задача, в якій роботи і ресурси (виконавці) виражаються в різних одиницях вимірювання.
Типовим прикладом такої задачі є організація випуску різнорідної продукції на устаткуванні різних типів.
Початкові параметри моделі розподільчої задачі:
· n – кількість виконавців;
· m – кількість видів виконуваних робіт;
· ai – запас робочого ресурсу виконавця 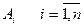 /од. ресурсу/;
/од. ресурсу/;
· bj – план по виконанню роботи 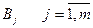 /од. робіт/;
/од. робіт/;
· cij – вартість виконання Bj роботи Ai виконавцем /грн./од. робіт/;
· λij – інтенсивність виконання Bj роботи Ai виконавцем /од.робіт/од.ресурсу/.
Шукані параметри моделі розподільчої задачі:
· xij – планове завантаження виконавця Ai при виконанні Bj робіт /до.ресурсу/;
· 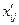 - кількість робіт, які повинен буде провести виконавець Ai /од.робіт/;
- кількість робіт, які повинен буде провести виконавець Ai /од.робіт/;
· L(X) – загальні витрати на виконання всього запланованого об’єму робіт /грн../.
ЕТАПИ ПОБУДОВИ МОДЕЛІ
I.Визначення змінних.
II. Побудова розподільчої матриці (таблиця1).
III.Задання цільової функції.
IV. Задання обмежень.
Таблиця 1.
| Виконавці | Роботи | Запас ресурсу од. ресурсу | |||||||
| B1 | B2 | … | Bm | ||||||
| A1 | λ11 | λ12 | … | λ1m | a1 | ||||
| c11 | c12 | … | c1m | ||||||
| A2 | λ21 | λ22 | … | λ2m | a2 | ||||
| c21 | c22 | … | c2m | ||||||
| … | … | … | … | … | … | ||||
| An | λn1 | λn2 | λnm | an | |||||
| cn1 | cn2 | cnm | |||||||
| План, од. роботи | b1 | b2 | … | bm |
Модель розподільчої задачі
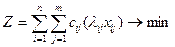
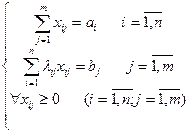 (7)
(7)
де 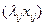 - це кількість робіт j – го виду, i – м виконавцем.
- це кількість робіт j – го виду, i – м виконавцем.
Етапи розв’язання розподільчої задачі
І. Перетворення розподільчої задачі в транпортну задачу:
1. вибір базового ресурсу і розрахунок нормованих продуктивностей ресурсів αi:
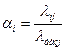
2. перерахунок запасу робочого ресурсу виконавців 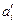 :
:
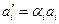 [од. ресурсу];
[од. ресурсу];
3. перерахунок планового завдання 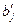 :
:

4. перерахунок собівартості робіт:
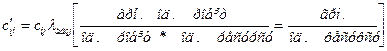
ІІ. Перевірка балансу перерахованих параметрів 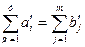 і побудова транспортної матриці.
і побудова транспортної матриці.
ІІІ. Пошук оптимального розв’язку транспортної задачі 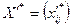 .
.
IV. Перетворення оптимального розв’язку транспортної задачі 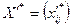 в оптимальний розв’язок розподільчої задачі, причому перехід виконується за формулою:
в оптимальний розв’язок розподільчої задачі, причому перехід виконується за формулою:
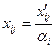 [од. ресурсу],
[од. ресурсу],
де 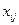 і
і 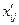 - відповідні елементи розв’язку розподільчої задачі і транспортної задачі.
- відповідні елементи розв’язку розподільчої задачі і транспортної задачі.
V. Визначення кількості робіт, відповідно оптимальному розв’язку розподільчої задачі Х*:
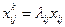
VI. Визначення цільової функції розподільчої задачі Z згідно з (7).
7. Приклад вирішення задачі типу ТЗ.
На фабриці працюють три типи ткацьких верстатів, які можуть випускати чотири види тканин. Відомі наступні дані про виробничій процес:
· продуктивність верстатів по кожному виду тканин, м/год 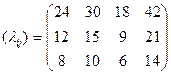
· собівартість тканини, грн./м 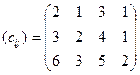
· ресурси робочого часу верстатів (ai): 90, 220, 180 год;
· запланований об’єм випуску тканин (bj): 1200, 900, 1800, 840 м.
Вимагається розподілити випуск тканини по верстатах так, щоб мінімізувати загальну собівартість виробництва тканин.
Питання для самоконтролю.
· Чому транспортну задачу вирішують іншими методами, якщо це задача лінійного програмування?
· Яка транспортна задача називається закритою?
· Що робити якщо транспортна задача відкрита?
· Дайте означення опорного плану транспортної задачі.
· Коли опорний план транспортної задачі не вироджений?
· Що робити, якщо опорний план транспортної задачі вироджений?
· Дайте означення оптимального опорного плану транспортної задачі.
· Сформулюйте необхідні і достатні умови існування розв’язку транспортної задачі.
· Як построїти потенціали строк і стовпців?
· В чому полягає метод північно-західного кута?
· В чому полягає метод найменших витрат?
· Як визначити, що опорний план оптимальний?
· Дайте означення циклу перерозподілу поставок.
Тема 4. Теорія двоїстості та аналіз лінійних моделей оптимізаційних задач.
Лекція 10.
Тема лекції: Двоїста задача лінійного програмування
Мета: ознайомити студентів з методами розв’язання двоїстих задач лінійного програмування, показати взаємозв’язок прямої та двоїстої задач.
План лекції
1. Математичні моделі двоїстих задач.
2. Основні теореми теорії двоістості.
3. Взаємозв’язок розв’язків прямої та двоїстої задач.
Література:
1. Лавріненко Н.М., Латинін С.М., Фортуна В.В., Безкровний О.І. Основи економіко-метематичного моделювання: Навч. Посіб. - Львів: «Магнолія 2006», 2010.- 540с.
2. Іванюта І. Д. Практикум з математичного програмування: Навчальний посібник / І. Д. Іванюта, В. І. Рибалка, І. А. Рудоміно-Дусятська. – К.: «Слово», 2008. - 296 с.
3. Кучма М. І. Математичне програмування: приклади і задачі: Навчальний посібник / М.І. Кучма. – Львів: «Новий Світ - 2000», 2006. - 344 с.
4. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1993. – 336 с.
1 Математичні моделі двоїстих задач.
З кожною задачею лінійного програмування зв’язана деяка інша цілком визначена, задача лінійного програмування яка називається двоїстою.
Початкова задача називається прямою задачею ЛП. Ці дві задачі тісно пов’язані між собою і утворюють єдину пару двоїстих задач.
Якщо пряма задача ЛП має вигляд:
Z=∑cixi →max (1)
за умов
∑aijxj ≤bi, (i=1,2…..m) (2)
xj ≥0 (j=1,2…..n) (3)
то двоїста задача записується так:
F=∑biyi →min (1*)
за умов
∑aijyi≥ cj, (j=1,2…..n) (2*)
yi≥0 (i=1,2…..m) (3*)
В матричному вигляді їх можна представити таким чином:
Пряма задача
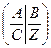 , xj ≥0 (j=1,2…..n)
, xj ≥0 (j=1,2…..n)
де А – матриця системи обмежень задачі розміром m x n;
В – вектор стовпець;
С – вектор строка;
АХ≤В;
Z →max.
Двоїста задача
tr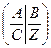 =
=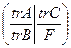 , yi ≥0 (i=1,2…..m)
, yi ≥0 (i=1,2…..m)
де trA – транспонована матриця А;
trС – транспонований вектор С;
trB - транспонований вектор В;
AY ≥trC;
F →min.
У несиметричних парах двоїстих задач обмеження прямої задачі можуть бути записані як рівняння (у канонічному вигляді), а двоїстої – лише як нерівності. Якщо у цільовій функції двоїстої задачі вимагається знайти мінімум, то система обмежень матиме знак «≥», якщо максимум, то знак «≥».
Моделі несиметричних пар цих задач можна зобразити у вигляді:
| Пряма задача | Двоїста задача |
| Z=∑cixi →max/min за умов ∑aijxj =bi, (i=1,2…..m) xj ≥0 (j=1,2…..n) | F=∑biyi →min/max за умов ∑aijyi≥/≤ cj, (j=1,2…..n) yi є(-∞,∞) (i=1,2…..m) |
Математична модель прямої задачі мішаної пари двоїстих задач містить обмеження, записані як рівняння, так і нерівності, причому знаків різних, за виглядом. Для складання двоїстої задачі необхідно привести всі нерівності системи обмежень прямої задачі до одного вигляду: якщо пряма задача на максимум, то всі нерівності обмежень приводимо до вигляду «≤», якщо на мінімум до вигляду «≥». Нерівності, для яких дані вимоги не виконуються, домножимо на (-1).
2. Основні теореми двоїстості.
Розглянемо пару даоїстих задач, утворену канонічною задачею ЛП і двоїстої до неї:
Пряма:
Z=∑cixi →max/min
за умов
∑aijxj =bi, (i=1,2…..m)
xj ≥0 (j=1,2…..n)
Двоїста:
F=∑biyi →min/max
за умов
∑aijyi≥/≤ cj, (j=1,2…..n)
yi є(-∞,∞) (i=1,2…..m)
Між прямою і двоїстою задачами ЛП існує тісний взаємозв’язок, який видно з наведених далі лем та теорем.
Лема 1. Якщо Х – деякий план прямої задачі, Y – довільний план двоїстої задачі, то значення цільової функції прямої задачі при плані Х не перевищує значення цільової функції двоїстої задачі при плані Y, тобто
Z(X)≤F(Y)
Лема 2. Якщо Z(X*)=F(Y*), та X* - оптимальний план прямої задачі, то Y* - оптимальний план двоїстої задачі.
Теорема 1. (перша теорема двоїстості). Якщо одна із пар двоїстих задач має оптимальний план, то і друга задача має оптимальний план і значення цільової функції при їх оптимальних планах рівні між собою, тобто Z(X*)=F(Y*).
Якщо ж цільова функція однієї із двоїстих задач необмежена (для прямої задачі - зверху, а для двоїстої з низу), то множина планів двоїстої задачі є порожньою.
Теорема 2. (друга теорема двоїстості). Для того щоб плани Х* і Y* відповідно до задач (1) – (3) і (1*) – (3*) були оптимальними планами цих задач, необхідно і достатньо, щоб для кожного j (j=1,2…..n) виконувалась рівність:
(a1j(y1)* + a2j(y2)* + ……. + amj(ym)* - cj)(xj)* = 0
Економічну інтерпретацію двоїстої задачі розглянемо на прикладі задачі про оптимальне використання ресурсів, математична модель якої має вигляд:
Z=∑cixi →max
за умов
∑aijxj =bi, (i=1,2…..m)
xj ≥0 (j=1,2…..n)
Двоїста задача до неї буде така:
F=∑biyi →min
за умов
∑aijyi≥ cj, (j=1,2…..n)
yi ≥0 i=1,2…..m
Приклад. Підприємство виготовляє три види продукції А,В,С.
Дані задачі приведені у таблиці:
| Види сировини | Норми витрат сировини (кг) | Запаси сировини | ||
| А | В | С | ||
| S1 | ||||
| S2 | ||||
| S3 | ||||
| Ціна від реалізації 1-ї одиниці продукції |
Знайти такий план випуску продукції, щоб прибуток від їх реалізації був максимальним.
3 Взаємозв’язок розв’язків прямої та двоїстої задач.
Розглянемо пару двоїстих задач ЛП (1) – (3) і (1)* - (3)*, пряма задача якої записана у канонічному вигляді. Наступна теорема встановлює взаємозв’язок між розв’язками прямої і двоїстої задачами.
Теорема 3. Якщо пряма задача ЛП має оптимальний план Х*, отриманий симплекс методом, то оптимальний план Y* двоїстої задачі визначається за формулою:
Y*=CбазР-1 (4)
де Cбаз – вектор рядок, що складається з коефіцієнтів цільової функції прямої задачі при невідомих, які є базисними в оптимальному плані; Р-1 – матриця, обернена до матриці Р, складеної з компонент базисних векторів оптимального плану задачі.
Таким чином, якщо знайти симплекс методом оптимальний план задачі (1) –(3), то використовуючи останню симплекс таблицю, можна визначити Cбаз і Р-1 та за допомогою співвідношення (5.4), знайти план двоїстої задачі.
Відмітимо, що існує взаємно-однозначна відповідність між змінними: основним змінним прямої задачі відповідають додаткові змінні двоїстої задачі і навпаки:
| Змінні прямої задачі | |||||||
| Основні | Додаткові | ||||||
| Х1 | Х2 | …….. | Хк | Хк+1 | Хк+2 | ………. | Хn |
| Yn-k+1 | Yn-k+2 | …….. | Yn | Y1 | Y2 | ……… | Yn-k |
| Додаткові | Основні | ||||||
| Змінні двоїстої задачі |
Ідея двоїстого симплексного методу полягає у зв’язку між розв’язуваннями прямої та двоїстої задач ЛП. Немає потреби окремо розв’язувати пряму задачу, а окремо двоїсту, оскільки розв’язок обох задач можна знайти за одними й тими самими симплекс таблицями, пам’ятаючи, що невідомим прямої задачі відповідають стовпчики таблиці, а невідомим другої – рядки таблиці.
Двоїстий симплекс метод використовується для знаходження розв’язку задачі ЛП, записаної у канонічному вигляді, для якої серед векторів Рj, складених з коефіцієнтів при невідомих у системі рівнянь, є рівно m одиничних.
Також цей метод можна використовувати для знаходження розв’язку задач ЛП, коли вільні члени системи рівнянь є довільними числами (для розв’язування задач симплекс методом числа bi припускались невід’ємними).
Питання для самоконтролю.
· Нехай є задача про оптимальне використання ресурсів. Дайте економічну інтерпретацію двоїстої задачі.
· Сформулюйте першу теорему двоїстості.
· Сформулюйте другу теорему двоїстості.
· Перечисліть ознаки взаємно двоїстих задач.
· Як по рішенню прямої задачі знайти рішення двоїстої задачі.
· В чому полягає ідея двоїстого симплекс методу.
· Який економічний зміст основних змінних двоїстої задачі?
· Який економічний зміст додаткових змінних двоїстої задачі?
· Який економічний зміст перевірки системи обмежень прямої задачі для знайденого оптимального плану?
· Що дає перевірка обмежень двоїстої задачі?
· Як проводиться аналіз стовбців останньої симплекс таблиці, для яких Δi>0?
Тема 5. Цілочислові та параметричні задачі лінійного програмування
Лекція 11.
Тема лекції: Задача цілочислового програмування.
Мета: ознайомити студентів з методами розв’язання задач цілочислового програмування.
План лекції
1. Постановка задачі цілочислового програмування.
2. Метод Гоморі.
3. Графічний метод розв’язання задачі цілочислового програмування.
Література:
1. Лавріненко Н.М., Латинін С.М., Фортуна В.В., Безкровний О.І. Основи економіко-метематичного моделювання: Навч. Посіб. - Львів: «Магнолія 2006», 2010.- 540с.
2. Іванюта І. Д. Практикум з математичного програмування: Навчальний посібник / І. Д. Іванюта, В. І. Рибалка, І. А. Рудоміно-Дусятська. – К.: «Слово», 2008. - 296 с.
3. Кучма М. І. Математичне програмування: приклади і задачі: Навчальний посібник / М.І. Кучма. – Львів: «Новий Світ - 2000», 2006. - 344 с.
4. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1993. – 336 с.
1. Постановка задачі цілочислового програмування.
Безліч економічних завдань вимагають цілочисельного рішення. До них належать завдання, у яких змінні величини означають кількість одиниць неподільної продукції (кількість верстатів при установці устаткування, розподіл судів по лініях, літаків по рейсам, обчислювальних машин в керуючому комплексі і т.д.).
У математичній моделі задачі цілочислового програмування як цільова функція так і система обмежень можуть бути лінійними, нелінійними і змішаними.
Ми будемо розглядати тільки лінійні задачі цілочислового лінійного програмування.
Задача цілочислового програмування формулюється так:
Z= 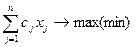 (1)
(1)
за умов
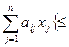 ,=
,=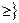 bi, i=
bi, i=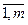 , (2)
, (2)
xj≥0, (j=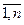 ), (3)
), (3)
xj - цілі, (j=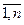 ), (4)
), (4)
умова цілочисельності (4), яка додається до звичайної задачі ЛП, суттєво ускладнює її розв’язання.
2. Метод Гоморі.
Сутність методу Гоморі (метод відтинання) полягає у тому, що спочатку розв’язується звичайна задача ЛП без урахування вимог цілочисельності змінних. Якщо отриманий оптимальний план задачі цілочисловий, то задача розв’язана. У протилежному випадку у модель вводиться спеціальне додаткове обмеження, що враховує цілочисельність змінних і володіє такими властивостями:
- вона повинна бути лінійною;
- вона повинна відтинати знайдений оптимальний нецілочисловий план задачі;
- не повинна відтинати ні одного цілочислового плану.
Додаткове обмеження, що має перелічені вище властивості, називається правильним відтинанням.
Це додаткове обмеження вводиться до оптимального плану якщо серед компонент оптимального плану є число з дробовую частиною. На базі цієї змінної будується додаткове обмеження Р.Гоморі:
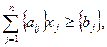
де 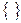 - дробова частина числа,
- дробова частина числа,
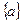 =а-[a].
=а-[a].
[a] – ціла частина числа а, т.б. найбільше ціле число, яке не перевищує числа а.
Якщо оптимальний план задачі має де кілька дробових значень, то додаткову нерівність складають для тієї змінної яка має найбільшу дробову частину.
Геометричний зміст кожного лінійного додаткового обмеження відповідає проведенню прямої (гіперплощини), яка відтинає від многокутника допустимих розв’язків деяку його частину разом із оптимальним нецілочисловим планом. Причому не відтинаються точки з цілими координатами цієї області допустимих розв’язків. У результаті область допустимих розв’язків послабленої задачі поступово зменшується доти, доки всі змінні оптимального плану не набувають цілочислових значень.
Алгоритм розязання задачі ЦП методом Гоморі:
· Розв’язуємо послаблену задачу ЛП (1)-(3) симплекс-методом. Якщо серед елементів оптимального плану (1)-(3) не має дробових чисел, то цей план і є розв’язком задач ЦП (1) – (4). Оптимальний план задачі (1) – (3) при цьому називається умовно-оптимальним для задачі (1) – (4). Якщо задача ЛП (1) – (3) не має розв’язків, то і задача ЦП (1) – (4) нерозв’язна.
· Якщо серед компонент умовно-оптимального плану є дробові, то серед них вибирається змінна, котра має найбільшу дробову частину. На основі цієї змінної формується додаткове обмеження Гоморі.
· Додаткове обмеження вводиться до останньої симплекс-таблиці, що містить умовно-оптимальний план задачі (1) – (3).
· Отриману розширену задачу вирішують симплекс-методом і перевіряють на цілочисловість. Якщо розв’язок не цілочисловий, то процедуру повторюють. Так діють до тих пір доти не буде знайдено рішення або не буде доведено, що задача не має допустимих розв’язків на множені цілих чисел.
3. Графічний метод розв’язання задачі цілочислового програмування.
Розглянемо графічний метод розв’язання задачі ЦП на прикладі.
Приклад 1. Знайти цілочисловий розвязок задачі ЛП
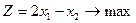
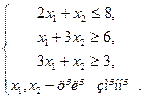
Розв’яжемо задачу ЦП методом Гоморі.
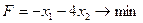
за умов
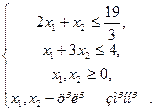
Питання для самоконтролю.
· Які економічні задачі належать до задач цілочислового програмування?
· Сформулюйте задачу ЦП.
· Перелічить основні етапи алгоритму Гоморі.
· В чому суть методу Гоморі?
· Як составити додаткове обмеження, якщо компоненти оптимального плану дробові?
· В якому випадку задача ЦЛП не має рішення?
· Який геометричний смисл має додаткове обмеження?
· Яке відтинання є правільним?
Тема 5. Цілочислові та параметричні задачі лінійного програмування
Лекція 12.
Тема лекції: Параметричне програмування.
Мета: ознайомити студентів з методами розв’язання задач параметричного програмування.
План лекції
1. Постановка задачі параметричного програмування.
2. Лінійне програмування з параметром у цільовій функції.
3. Задачі з параметром у правій частині системи обмежень.
Література:
1. Лавріненко Н.М., Латинін С.М., Фортуна В.В., Безкровний О.І. Основи економіко-метематичного моделювання: Навч. Посіб. - Львів: «Магнолія 2006», 2010.- 540с.
2. Іванюта І. Д. Практикум з математичного програмування: Навчальний посібник / І. Д. Іванюта, В. І. Рибалка, І. А. Рудоміно-Дусятська. – К.: «Слово», 2008. - 296 с.
3. Кучма М. І. Математичне програмування: приклади і задачі: Навчальний посібник / М.І. Кучма. – Львів: «Новий Світ - 2000», 2006. - 344 с.
4. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1993. – 336 с.
1. Постановка задачі параметричного програмування.
Параметричне програмування являє собою один з розділів математичного програмування, вивчає завдання, в яких цільова функція або обмеження залежать від одного або кількох параметрів.
Необхідність розгляду подібних завдань обумовлена різними причинами. Однією з основних є та, що вихідні дані для чисельного рішення будь-якої реальної задачі оптимізації в більшості випадків визначаються наближено або може змінюватися під впливом якихось чинників, що може істотно позначитися на оптимальності вибираної програми (плану) дій. Відповідно, розумно вказувати не конкретні дані, а діапазон можливої зміни даних, що б в результаті рішення мати найкращі плани для будь-якого варіанту вихідних даних.
З математичної точки зору параметричне програмування виступає як один із засобів аналізу чутливості рішення до варіації вихідних даних, оцінки стійкості рішення.
Зауважимо, що існують різні підходи до подібного аналізу (наприклад, на основі постановки двоїстої задачі). Тут ми, не посилаючись на двоїсті оцінки, розглянемо найпростіші варіанти рішення для самих найпростіших параметричних задач.
Параметрична задача може бути записана так:
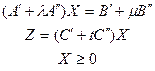
де 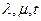 - числові параметри, які належать відрізку або всій числовій осі, або заданим відрізкам цієї осі.
- числові параметри, які належать відрізку або всій числовій осі, або заданим відрізкам цієї осі.
Якщо 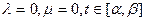 , то маємо задачу з параметром у цільовій функції.
, то маємо задачу з параметром у цільовій функції.
Якщо  , то це задача з параметром у правій частині системи обмежень.
, то це задача з параметром у правій частині системи обмежень.
Якщо  , то це задача з параметром у лівій частині системи обмежень.
, то це задача з параметром у лівій частині системи обмежень.
2. Лінійне програмування з параметром у цільовій функції.
Розглянемо задачу параметричного лінійного програмування, в якій тільки коефіцієнти цільової функції лінійно залежать від деякого єдиного параметра λ (часу, температури і т. п.):
Відшукати максимум (або мінімум) функції:
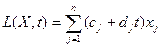
за умов
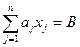
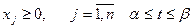
Якщо звернутися до геометричної інтерпретації задачі, то можна помітити, що вектор-градієнт лінійної форми визначається її параметром. Наприклад, для цільової функції L(х,t) = tх1 + (1-t) х2 при різних значеннях параметра t градієнт визначає різні напрямки зростання функції.
Неважко бачити, що, якщо при деякому значенні параметра максимум досягається в вершині A, то невелика варіація цього значення дещо змінить напрямок градієнта, але не змінить положення точки максимуму. Звідси напрошується висновок, що деякий план, оптимальний при t = t0 оптимальний і в околиці t0, тобто при α ≤ t ≤ β де t0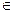 [α, β].
[α, β].
Можна помітити, що при градієнті, що став перпендикулярним деякої сторони багатокутника планів, маємо два різних оптимальних опорних плани з одним і тим же значенням лінійної форми, звідки можна стверджувати безперервність екстремуму лінійної форми за t.
У разі необмеженість безлічі планів можна стверджувати, що якщо лінійна форма не обмежена при t = t0, то вона не обмежена при всіх t, більших або менших t0.
Алгоритм для вирішення завдань параметричного лінійного програмування в разі залежності від параметра коефіцієнтів цільової функції незначно відрізняється від звичайного симплексного методу.
Приклад 1. Геометрична інтерпритація розв’язку задачі з параметром у цільовій функції.
Підприємство повинне випустити два види продукції А і В, для використання яких використовуються три види сировини. Норма витрат та запаси кожного виду сировини на виробництво даного виду продукції наведені у таблиці 1. Відомо, що ціна одиниці продукції може змінюватися із часом і визначається співвідношеннями (2+t) для продукції А і (10-t) для продукції В, де 0≤t≤10. Потрібно визначити план виробництва, при якому загальна вартість продукції буде максимальною.
Таблиця 1.
| Види продукції | Норми витрат на од. продукції, т. | Запаси сировини | |
| А | В | ||
3. Задачі з параметром у правій частині системи обмежень.
У разі залежності від параметра компонент вектора правих частин обмежень, тобто рішення задачі пошуку екстремуму функції
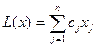
за умов
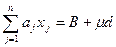
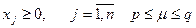
 2014-02-04
2014-02-04 1257
1257








