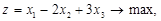
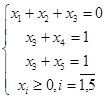
За початковий базис можна вибрати Р1, Р4, Р5 або Р2, Р4, Р5, тоді початковий опорний план Х=(0,0,0,1,1) є виродженим, так як базисна змінна х1=0 або х2=0. Для обох початкових планів z=0, тобто у випадку виродженності значення цільової функції може повторюватись навідь при зміні базису.
Поточний базисний розв’язок може стати виродженим, якщо виникає невизначеність у виборі ключового рядка, тобто одержуємо однакове мінімальне значення симплексного відношення
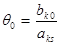 для декількохзначень k, де s – номер вектора, який вводять до базису. У цьому випадку також при зміні складу базисних змінних значення цільової функції буде залишатись незмінним.
для декількохзначень k, де s – номер вектора, який вводять до базису. У цьому випадку також при зміні складу базисних змінних значення цільової функції буде залишатись незмінним.
Оскільки число наборів векторів скінченне, то після деякого числа ітерацій дійдемо до одного з висновків:
1. розв’язок оптимальний;
2. задача не розв’язувана;
3. отриманий базисний розв’язок був на попередніх ітераціях. Це значить, що процес обчислення зациклився, тобто після ряду ітерацій ми повертаємося до раніше використаного базису.
Тема 2. Загальна задача лінійного програмування та деякі з методів її розв’язування
Лекція 6
Тема лекції: Розв’язання задач ЛП симплекс-методом (продовження)
Мета: ознайомити студентів з методами розв’язання задач ЛП симплекс – методов із стандартним базисом, симплекс-методом зі штучним базисом.
План лекції
4. Правило уникнення зациклювання при застосуванні симплекс-методу.
5. Метод штучної базиси розв’язування задач ЛП.
6. Приклад вирішення задачі ЛП методом штучної бази.
Література:
1. Лавріненко Н.М., Латинін С.М., Фортуна В.В., Безкровний О.І. Основи економіко-метематичного моделювання: Навч. Посіб. - Львів: «Магнолія 2006», 2010.- 540с.
2. Іванюта І. Д. Практикум з математичного програмування: Навчальний посібник / І. Д. Іванюта, В. І. Рибалка, І. А. Рудоміно-Дусятська. – К.: «Слово», 2008. - 296 с.
3. Кучма М. І. Математичне програмування: приклади і задачі: Навчальний посібник / М.І. Кучма. – Львів: «Новий Світ - 2000», 2006. - 344 с.
4. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1993. – 336 с.
4. Правило уникнення зациклювання при застосуванні симплекс-методу.
Якщо на будь якому етапі розрахунків виникає невизначеність у виборі ключового рядка, тобто виявляється кілька однакових мінімальних симплексних відношень, то необхідно вибирати рядок, для якого відношення елементів наступного стовпчика, що не входить у базис, до відповідних елементів ключового стовпчика є найменшим. При цьому ділення необхідно виконувати і на від’ємні елементи, тобто отримані відношення можуть бути від’ємними.
Якщо, при цьому знову виявляються однакові мінімальні симплексні відношення, то складають відношення елементів наступного стовпчика, і так роблять доти, доки ключовий рядок не визначиться однозначно.
Приклад 2. Вирішити задачу ЛП
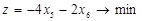
за умов
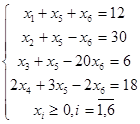
5. Метод штучної базиси розв’язування задач ЛП.
Застосовується у тих випадках, коли в вихідній задачі ЛП, яка записана у канонічному вигляді, в системі обмежень немає необхідної кількості одиничних ортогональних незалежних векторів Pj, тобто важко вказати початковий опорний план.
М-метод полягає у використанні правил симплекс – методу до так званої задачі ЛП. Вона отримується із початкової додованням до лівої частини системи рівнянь таких штучних одиничних векторів з відповідними невід’ємними штучними змінними, щоб знову отримати m одиничних ортогональних лінійно незалежних векторів.
У цільовій функції задачі ЛП штучні змінні мають коефіцієнт - М (f(x)→max) або +М (f(x)→min), де під М ми розуміємо досить велике додатне число.
При розв’язанні цієї задачі симплекс-методом оцінки Δj будуть залежити від М. Для порівняння оцінок, треба пам’ятати, що М – достатньо велике додатне число, тому із базису будуть виключатися у першу чергу штучні вектори.
Якщо із базису всі штучні вектори вийшли, то ми отримали вихідну задачу.
Якщо оптимальний розв’язок М – задачі містить штучні змінні або М – задача нерозв’язна, то початкова задача також нерозв’язна.
6. Приклад вирішення задачі ЛП методом штучної бази.
Інвестиційна компанія має на своєму рахунку 5 млн. грн. Розглядаються чотири види інвестицій – державні цінні папери, цінні папери корпорацій, акції сфери обслуговуння та акції виробничої сфери. Державні цінні папери належать до без ризикових, решта інвестицій – до ризикових. Метою інвестиційної компенії є максимізація прибутку. Прибуток від інвестицій становить відповідно – 5%, 8%, 10% та 12%. Гроші які не інвестуються, залишаються на банківському рахунку і дають прибуток 1%. Менеджер з інвестицій ухвалив рішення, що не менше ніж 2 млн. грн. слід розмістити у цінні папери корпорацій, а в інвестиційні проект из елементами ризику потрібно вкласти не більше ніж 4 млн. грн.
Визначити оптимальний інвестиційний портфель, суму грошей, яка залишиться на банківському рахунку, а також річний прибуток від реалізації цього портфеля.
Питання для самоконтролю.
· В чому полягає симплекс-метод із стандартним базисом?
· Поясніть основну ідею симплекс-методу.
· Як визначити початковий опорний план задачі ЛП?
· Дайте економічну інтерпретацію критерію оптимальності опорного плану та правила переходу до нового базису.
· Як визначається вектор для введення у базис, якщо опорний план неоптимальний?
· Як визначається вектор, що виводиться із базису?
· Сформулюйте ознаку нерозв’язності задачі ЛП у симплекс-методі.
· Коли використовують симплекс-метод зі штучним базисом?
· Принципи заповнення симплекс-таблиці.
· Що таке розв’язувальний елемент симплекс-таблиці?
· Як перевірити опорний план на оптимальність?
· Поясніть метод Жордана-Гауса.
· Що таке штучні змінні?
Тема 3. Транспортна задача.
Лекція 7
Тема лекції: Транспортна задача
Мета: ознайомити студентів з основними теоремами та методами розв’язання транспортної задачі
План лекції
1. Економічна та математична моделі транспортної задачі.
2. Основні теореми транспортної задачі.
3. Метод північно-західного кута (діагональний).
4. Метод найменших витрат.
Література:
1. Лавріненко Н.М., Латинін С.М., Фортуна В.В., Безкровний О.І. Основи економіко-метематичного моделювання: Навч. Посіб. - Львів: «Магнолія 2006», 2010.- 540с.
2. Іванюта І. Д. Практикум з математичного програмування: Навчальний посібник / І. Д. Іванюта, В. І. Рибалка, І. А. Рудоміно-Дусятська. – К.: «Слово», 2008. - 296 с.
3. Кучма М. І. Математичне програмування: приклади і задачі: Навчальний посібник / М.І. Кучма. – Львів: «Новий Світ - 2000», 2006. - 344 с.
4. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1993. – 336 с.
1 Економічна та математична моделі транспортної задачі.
Транспортна задача одна з найпоширеніших задач лінійного програмування. Її мета – розробка найбільш раціональних шляхів і способів транспортування однорідної продукції від постачальників до споживачів.
Транспортна задача – це специфічна задача лінійного програмування, яка застосовується для визначення найекономічнішого плану перевезення однорідної продукції від постачальників до споживачів.
У загальному вигляді транспортну задачу можна сформулювати так: в m пунктах постачання А1,А2,…… Am (надалі постачальники) міститься однорідна продукція у кількості відповідно а1, а2,….. аm. Цю продукцію потрібно перевезти в n пункти призначення B1,B2,…… Bn (надалі споживачі) у кількості відповідно b1, b2,….. bn. Вартість перевезення одиниці товару (тариф) із пункту Аi в пункт Bj дорівнює сji.
Математична модель транспортної задачі має такий вигляд:
F(xji)= ∑∑ xji сji→ min (1)
за умов
∑xji =ai (i=1,2…..m) (2)
∑xji =bj (j=1,2…..n) (3)
xji≥0 (i=1,2…..m; j=1,2…..n) (4)
Алгоритм і методи розв’язання транспортної задачі можна використати для знаходження розв’язку деяких економічних задач, які не мають нічого спільного з транспортуванням вантажів. У цьому разі величини тарифів перевезення сji мають різний зміст залежно від конкретної задачі. До таких задач належать наступні:
· Оптимальне закріплення за верстатами операцій з обробки деталей. У них сji означає продуктивність праці.
· Розміщення сільськогосподарських культур за ділянками землі різної врожайності.
· Оптимальні призначення або проблема вибору.
· Задача про скорочення виробництва із врахуванням загальних витрат на виготовлення і транспортування продукції
· Збільшення продуктивності автомобільного транспорту за рахунок мінімізації порожнього пробігу
2 Основні теореми транспортної задачі.
Означення 1. Якщо у транспортної задачі виконується умова балансу
∑bj = ∑ai (5)
То задача називається закритою або збалансованою.
Означення 2. Планом транспортної задачі називається сукупність величин xji (i=1,2…..m; j=1,2…..n), який задовольняє умови обмеження (2) – (4).
Означення 3. Опорний план транспортної задачі називається не виродженим, якщо він містить N=m+n-1 додатних елементів xji
Означення 4. Якщо опорний план містить менше N<m+n-1 додатних елементів, то він називається виродженим.
Означення 5. Оптимальним планом транспортної задачі називають матрицю Х*, яка задовольняє умови задачі (2) – (4) і для якої цільова функція F набуває мінімального значення.
Теорема 1. (Необхідна і достатня умова існування розв’язку задачі ТЗ).
Транспортна задача має розв’язок тоді і тільки тоді, коли вона збалансована, тобто виконується умова (5).
Теорема 2. Для того щоб деякий план Х транспортної задачі був оптимальним необхідно і достатньо, щоб йому відповідала така система із m+n чисел ui (i=1,2…..m) vj (j=1,2…..n) для якої виконуються умови
vj - ui = сji для xji>0
vj - ui ≤ сji для xji=0.
Означення 6. Числа vj та ui називаються потенціалами строк та стовпців.
3. Метод північно-західного кута (діагональний.)
Побудова опорного плану задачі починають із заповнення верхньої клітинки таблиці x11, в яку записують менше з двох чисел a1 та b1.
Далі переходять до наступної клітинки в рядку або стовпчику і заповнюють ії і т.д. Закінчують заповнювати таблицю у правій нижній клітинці.
Зауважемо, що користуючись методом північно-західного кута початковий опорний план залежить від величин ai та bj і зовсім не залежить від вартостей перевезення сji, а тому він буде далекий від оптимального.
4. Метод найменшої вартості.
Сутність цього методу полягає у тому, що на кожному кроці заповнюють клітинки таблиці, яка має найменшу вартість перевезеня одиниці продукції між постачальниками та споживачами.
Приклад 1. Отримати початковий опорний план транспортної задачі методом північно-західного кута та методом найменшої вартості.
Тема 3. Транспортна задача.
Лекція 8
Тема лекції: Транспортна задача (продовження)
Мета: ознайомити студентів з основними теоремами та методами розв’язання транспортної задачі
План лекції
5. Метод потенціалів.
6. Приклад вирішення транспортної задачі.
7. Ускладнені задачі транспортного типу.
Література:
1. Лавріненко Н.М., Латинін С.М., Фортуна В.В., Безкровний О.І. Основи економіко-метематичного моделювання: Навч. Посіб. - Львів: «Магнолія 2006», 2010.- 540с.
2. Іванюта І. Д. Практикум з математичного програмування: Навчальний посібник / І. Д. Іванюта, В. І. Рибалка, І. А. Рудоміно-Дусятська. – К.: «Слово», 2008. - 296 с.
3. Кучма М. І. Математичне програмування: приклади і задачі: Навчальний посібник / М.І. Кучма. – Львів: «Новий Світ - 2000», 2006. - 344 с.
4. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1993. – 336 с.
5. Метод потенціалів.
Після перевірки транспортної задачі на сбалансованість та визначення початкового плану транспортної задачі приступаємо до розрахунку потенціалів строк і стовпців для заповнених кліток:
vj - ui = сji для xji>0 (6)
Оскільки заповнених клітинок є m+n-1, то система рівнянь (6) із m+n невідомих містить m+n-1 рівнянь. Прийнявши одне невідоме за нуль, наприклад, u1=0, решту знаходимо.
Для побудованого опрного плану і знайдених потенціалів обчислюємо оцінки вільних клітинок:
Δji =vj - ui - сji
Якщо, Δji ≤0, то побудований опрний план є оптимальним.
Якщо, хоча б для однієї клітинки ця умова не виконується, то опорний план не є оптимальним і треба від нього переходити до нового опорного плану.
Перехід від одного опорного плану до іншого здійснюється заповненням клітинки, для якої порушено умови оптимальності. Якщо таких клітинрк кілька, то для заповнення вибіраютьтаку, що має найбільшє порушенняі з неї будують цикл перерозподілу.
Означення 7. Циклом у транспортної задачі називають замкнену ламану лінію, вершини якої розміщуються в заповнених клітинках таблиці, а сторонни проходять уздовж рядків і стовпчиків таблиці.
Для вибраної вільної клітинки і клітинок, що пов’язані з нею циклом, здійснюють перерозподіл продукції в межах цього циклу за такими правилами:
· Кожній вершині циклу приписують певний знак, причому вільній клітинці – знак «+», а всім іншим по черзі- знаки «-» та «+»;
· У поржню клітинку переносять менше з чисел xji, що стоять у клітинках зі знком «-». Одночасно це число додають до відповідних чисел, які розміщені в клітинках зі знаком «+».
6. Приклад вирішення транспортної задачі.
Приклад 1. Розв’язати транспортну задачу.
| ui | |||||||||||
| vj |
7. Ускладнені задачі транспортного типу.
Дуже часто при складанні математичної моделі задачі транспортного типу доводиться враховувати цілу низку додаткових обмежень, а потім застосовувати метод потенціалів.
Розглянемо ситуації, які зустрічаються найчастіше:
· Заборона на постачання від i-го до j – го споживача. Якщо окремі поставки від визначених постачальників до певних споживачів повинні бути виключені з плану перевезень, то це досягається штучним завищенням за цим маршрутом транспортних витрат (якщо витрати мінімізуються). Тобто тариф на перевезення за цим маршрутом покладається рівним деякому великому числу М.
· Фіксовані постачання, тобто певний обсяг поставок за деяким маршрутом обов’язково повинен ввійти в оптимальний план перевезень незалежно від вигідності. Наприклад, за маршрутом 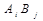 необхідно перевезти рівно d одиниць вантажу. У цьому випадку зменшують запас вантажу у відповідного постачальника
необхідно перевезти рівно d одиниць вантажу. У цьому випадку зменшують запас вантажу у відповідного постачальника 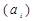 і попит відповідного споживача
і попит відповідного споживача 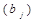 на величину обов’язкової поставки d, а також вводять заборону на постачання за маршрутом
на величину обов’язкової поставки d, а також вводять заборону на постачання за маршрутом 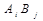 і далі розв’язується отримана задача. Отриманий методом потенціалів розв’язок
і далі розв’язується отримана задача. Отриманий методом потенціалів розв’язок 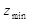 коригується з урахуванням цієї обов’язкової поставки і отримують
коригується з урахуванням цієї обов’язкової поставки і отримують 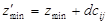 .
.
· Обмеження на мінімальні постачання. Якщо за маршрутом 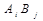 необхідно перевезти не менше d одиниць вантажу, то в цьому випадку, аналогічно, як і при фіксованих постачаннях, зменшуються на величину d запаси відповідного постачальника і попит споживача. Але в цьому випадку не вводиться заборона на постачання за маршрутом
необхідно перевезти не менше d одиниць вантажу, то в цьому випадку, аналогічно, як і при фіксованих постачаннях, зменшуються на величину d запаси відповідного постачальника і попит споживача. Але в цьому випадку не вводиться заборона на постачання за маршрутом 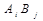 .
.
· Обмеження на перепускні спроможності за певним транспортним маршрутом. Наприклад, за маршрутом 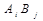 можна перевезти не більше d одиниць вантажу. Тоді
можна перевезти не більше d одиниць вантажу. Тоді 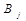 - й стовпчик розбивається на два
- й стовпчик розбивається на два 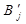 та
та 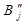 з попитом, який складає
з попитом, який складає 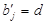 і
і 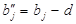 відповідно. Транспортні тарифи в нових стовпчиках такі ж, але в клітині
відповідно. Транспортні тарифи в нових стовпчиках такі ж, але в клітині 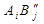 ставиться штучно завищений (блокующий) тариф. У оптимальному плані перевезень ці два стовпчики знову об’єднують в один.
ставиться штучно завищений (блокующий) тариф. У оптимальному плані перевезень ці два стовпчики знову об’єднують в один.
Приклад 2. Розвязати транспортну задачу:
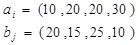
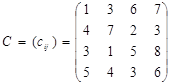
Додаткова умова: попит третього споживача задовольнити повністю за маршрутом 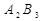 перевезти рівно 10 од. продукції.
перевезти рівно 10 од. продукції.
Тема 3. Транспортна задача.
Лекція 9
Тема лекції: Транспортна задача (продовження)
Мета: ознайомити студентів з основними теоремами та методами розв’язання транспортної задачі
План лекції
8. Задача про призначення.
9. Розподільчі задачі загального типу.
10. Приклад вирішення задачі типу ТЗ.
Література:
1. Лавріненко Н.М., Латинін С.М., Фортуна В.В., Безкровний О.І. Основи економіко-метематичного моделювання: Навч. Посіб. - Львів: «Магнолія 2006», 2010.- 540с.
2. Іванюта І. Д. Практикум з математичного програмування: Навчальний посібник / І. Д. Іванюта, В. І. Рибалка, І. А. Рудоміно-Дусятська. – К.: «Слово», 2008. - 296 с.
3. Кучма М. І. Математичне програмування: приклади і задачі: Навчальний посібник / М.І. Кучма. – Львів: «Новий Світ - 2000», 2006. - 344 с.
4. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1993. – 336 с.
 2014-02-04
2014-02-04 610
610







