Могут быть жесткими и гибкими

Дополнительные обратные связи

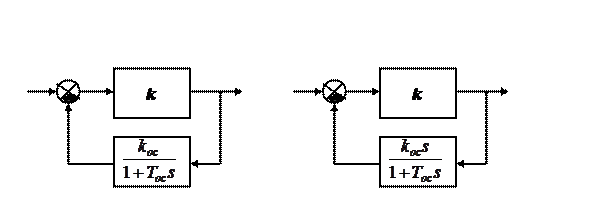
Синтез САР методом логарифмических частотных характеристик.

В системах регулирования и управления обычно задается объект управления. Если, кроме того, задана структура регулятора и корректирующих средств, то задача синтеза сужается до выбора параметров регулятора и корректирующих средств, исходя из поставленных требований.

При синтезе корректирующих устройств исходят из того, что объект регулирования – неизменяемая часть, а синтезу подлежат корректирующие устройства и регулятор – изменяемая часть системы. Для решения задачи в такой постановке весьма эффективными оказываются частотные методы, использующие ЛЧХ.

Синтез корректирующих устройств САР можно считать состоящим из 5 этапов:

- построения ЛЧХ исходной нескорректированной системы;

- построения желаемых ЛЧХ;

- определения вида и параметров корректирующих устройств;

- технической реализации корректирующих устройств;

- проверочного расчета системы с построением переходного процесса.

Существует несколько подходов к частотным методам синтеза, различающихся построением желаемых характеристик.

Для минимально-фазовых и нескольких не минимально-фазовых систем ограничиваются построением лишь одной логарифмической амплитудной характеристики. Рассмотрим рекомендации по формированию желаемой ЛАХ.

1. Вид низкочастотной области ЛАХ определяет главным образом точность работы САР. Среднечастотная область, прилегающая к частоте среза _с, определяет в основном запас устойчивости, т. е. качество переходных процессов. Высокочастотная область лишь незначительно влияет на качество процессов управления.

2. Желаемая ЛАХ в возможно большем интервале частот должна совпадать с ЛАХ исходной не скорректированной системы. Иначе реализация КУ может существенно усложниться.

3. В низкочастотной области наклон желаемой ЛАХ должен составлять -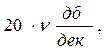где n- порядок астатизма. Желаемая ЛАХ на частоте 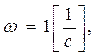имеет ординату 20lgK_n, где K_n -общий коэффициент усиления разомкнутой системы.

Если задана допустимая ошибка e_max при гармоническом входном воздействии g(t)=g_maxSinw_gt, то желаемая ЛАХ должна располагаться выше контрольной точки А_к, имеющей на частоте w_g ординату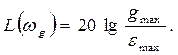

Если задана допустимая ошибка e_max, и оговорены только максимальная скорость W1_max и максимальное ускорение a_1max входного воздействия, то может быть подобрано эквивалентное гармоническое входное воздействие, у которого амплитуды скорости и ускорения равны максимальным заданным значениям, т.е.

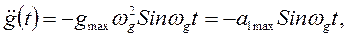
откуда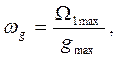 и, подставляя во второе, получим

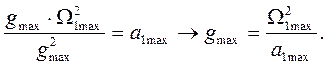Откуда

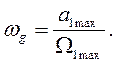
В этом случае ордината контрольной точки

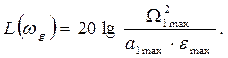
При задании W1_max, a_1max может быть получена так называемая запретная зона для низкочастотной части ЛАХ. Для этого нужно построить семейство контрольных точек, у которых амплитуда скорости по прежнему равна максимальному значению,

а амплитуда ускорения менее максимального и наоборот, когда амплитуда ускорения равна максимальному значению, а амплитуда скорости - меньше. Семейство этих точек образует две прямые с наклоном 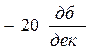в первом и 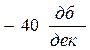во втором случае, пересекающиеся на частоте w_g..

При этом следует помнить, что действительная (не асимптотическая) желаемая ЛАХ проходит в точке излома на 3 дб ниже. Поэтому для предотвращения захода желаемой ЛАХ в запретную зону ее следует приподнять над контрольной точкой на 3 дб = 20lg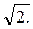

4. В районе среза w_с наклон желаемой ЛАХ выбирается равным 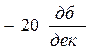, что позволяет обеспечить необходимый запас устойчивости. Чем больше протяженность участка с наклоном 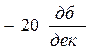, тем больше запас устойчивости, т.е. выше качество переходного процесса.

Рассмотрим, каким образом связана протяженность этого участка с показателем колебательности М.

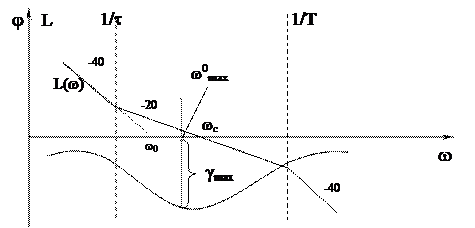
В области средних частот желаемой ЛАХ (см. рис.) соответствует передаточная функция

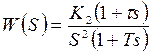, где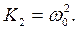

Фазовая характеристика в этой области частот имеет вид

.

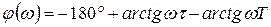Запас по фазе g(w)

т.е. (*),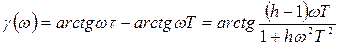

где 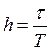- протяженность участка ЛАХ с наклоном .

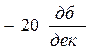Наибольший требуемый запас по фазе при оценке запаса устойчивости по показателю колебательности М

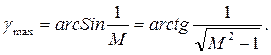
Он должен иметь место на частоте

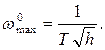
Подставляя в (*), получим

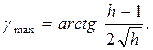
Приравнивая выражения для g_max, найдем наименьшую протяженность участка h, необходимую для получения требуемого показателя колебательности М

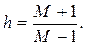
При М=1,5 имеем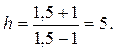

Так как на частоте 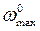модуль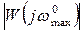

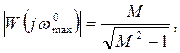то

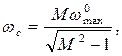
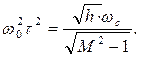
Следовательно,

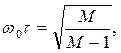
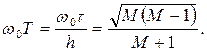
Отсюда видно, что для получения заданного показателя колебательности М необходимо иметь

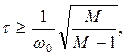
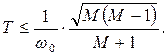
Полученные соотношения изменяться, если учитывать малые постоянные времени, расположенные в области высоких частот. В этих случаях

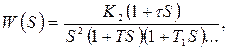и следует пользоваться формулами

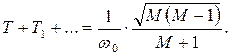
Если система содержит колебательное звено

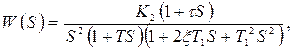
причем 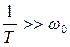, то в сумму постоянных времени включается величина 2xT_1. Кроме того, необходимо проверить, не возникает ли вблизи частоты 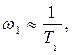где имеет место резонансный пик ЛАХ, вторая запретная зона для фазовой характеристики системы и не заходит ли фазовая характеристика в эту зону.

Если 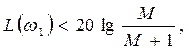то такая запретная зона отсутствует.

Быстродействие САР в этих случаях легко оценивается по значению частоты среза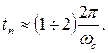

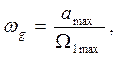
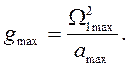
На частоте w_g –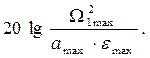

Синтез последовательных корректирующих устройств.

При синтезе последовательных КУ различают три способа коррекции, соответствующие трем основным последовательным КУ - замедляющему, форсирующему и интегро-дифференцирующему.

Рассмотрим на примере синтеза простейшей следящей системы (см. примеры)

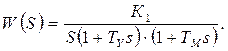
Если требования к быстродействию не очень высоки, то запретная зона по точности для ЛАХ располагается в области сравнительно низких частот, w_g мало.

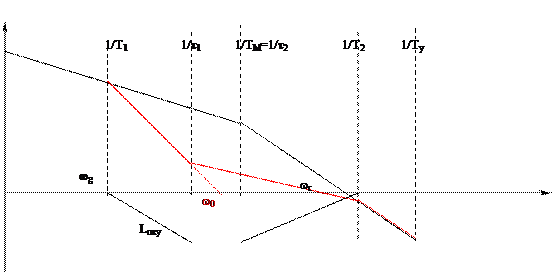
В этом случае взаимное расположение исходной L и желаемой Lж ЛАХ на рис.

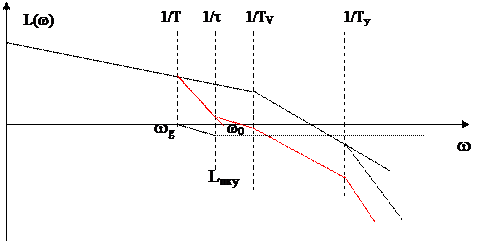Разностная ЛАХ 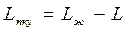соответствует ЛАХ замедляющего последовательного звена, имеющего передаточную функцию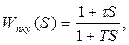

где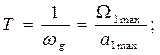

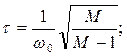
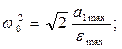
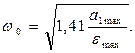
В результате коррекции деформируется низкочастотная часть ЛАХ. При этом происходит уменьшение усиления на низких частотах. Таким образом здесь осуществляется амплитудная коррекция САР. Изменение ФЧХ не существенно.

Разностная ЛАХ 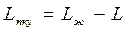соответствует интегро-дифференцирующему звену при увеличении w_g.

,

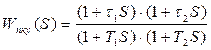где 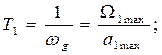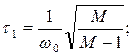t₂=T_M;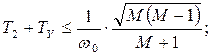

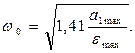
В этом случае деформируется среднечастотная часть ЛАХ, и происходит амплитудное подавление на средних частотах, т.е. амплитудная коррекция.

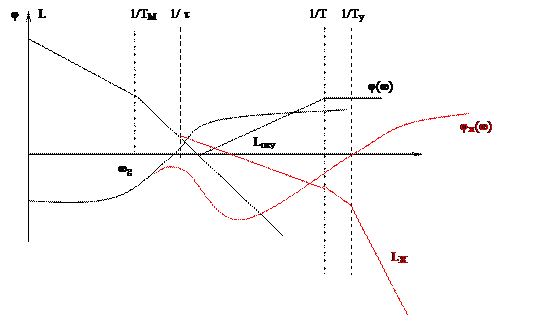
При большем увеличении w_g разностная ЛАХ 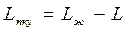соответствует последовательному включению форсирующего звена с передаточной функцией ,

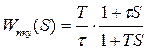где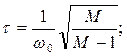

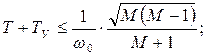
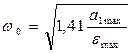
и дополнительного усилителя с коэффициентом усиления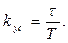

При такой коррекции происходит деформация в средне- и высокочастотной области. Однако эффект из-за деформации фазовой характеристики. Поэтому говорят о фазовой коррекции путем опережения в области средних частот.