Рассмотрим теперь частотные характеристики звена. Амплитудно-фазовая характеристика

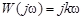
совпадает с положительной мнимой полуосью комплексной плоскости; вещественная частотная характеристика равна нулю, 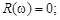мнимая частотная характеристика соответствует выражению

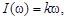
т. е. представляет собой линейно нарастающую функцию. С ней совпадает амплитудная частотная характеристика, которая имеет вид

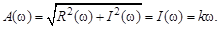
Фазовую частотную характеристику можно определить по соотношению

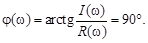
Следовательно, на всех частотах имеется постоянный фазовый сдвиг.

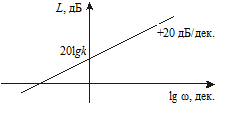
Рис. 3.6. Логарифмическая амплитудная
частотная характеристика дифференци-
рующего звена

Логарифмическая частотная характеристика следующая:

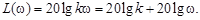(3.9)

Как видно из графика рис. 3.6, дифференцирующее звено усиливает высокочастотные сигналы.

3.1.3. Интегрирующее звено

Интегрирующим называется звено, поведение которого описывает уравнение

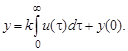(3.10)

Примером интегрирующего звена является операционный усилитель в режиме интегрирования.

Основной динамической характеристикой звена является его дифференциальное уравнение

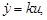(3.11)

на основе которого можно получить передаточную функцию

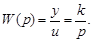(3.12)

Характеристическое уравнение

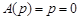
имеет единственный корень (полюс), 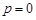, который представляет собой модальную характеристику интегрирующего звена.

Переходная характеристика звена имеет вид линейно возрастающей функции

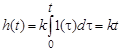1(t), (3.13)

а импульсная переходная функция – ступенчатой функции

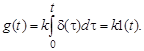(3.14)

Выражение для амплитудно-фазовой частотной характеристики (рис. 3.7) получим, заменив в (3.12) 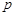на :

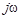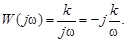
Вещественная частотная характеристика отсутствует, 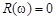. Мнимая частотная характеристика имеет вид

,

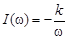а амплитудная частотная характеристика

.

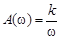При этом фазовая частотная характеристика следующая:

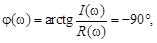(3.15)

т. е. звено имеет постоянный фазовый сдвиг, который не зависит от частоты.

Амплитудно-фазовая характеристика интегрирующего звена имеет вид прямой, совпадающей с отрицательной мнимой полуосью комплексной плоскости (рис. 3.7).

Запишем выражение для логарифмической амплитудно-частот-ной характеристики

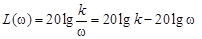(3.16)

и изобразим ее график (рис. 3.8).

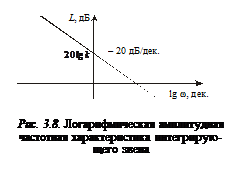Как видим, логарифмическая амплитудная частот-
ная характеристика интегра-
тора представляет собой пря-мую с наклоном – 20 дБ/дек.и пересекает ось ординат в точке 20 lg k. Она показывает, что звено усиливает низкочастотные сигналы и ослабляет высокочастотные.

3.1.4. Апериодическое звено

Апериодическим называется звено, дифференциальное уравнение которого имеет вид

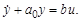(3.17)

Различного типа двигатели являются примерами такого звена.

Дифференциальное уравнение апериодического звена принято записывать в стандартном виде:

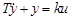, (3.18)

где 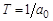– постоянная времени; 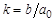– коэффициент усиления звена.

Заменив в (3.18) 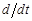на p, перейдем к символической записи дифференциального уравнения

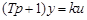(3.19)

и найдем передаточную функцию апериодического звена:

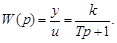(3.20)

Для определения модальных характеристик по передаточной функции (3.20) запишем характеристическое уравнение

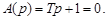(3.21)

Оно имеет единственный корень (полюс),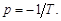

Переходную характеристику звена (рис. 3.9) можно найти как решение уравнения (3.18) пр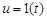и и :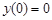

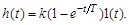(3.22)

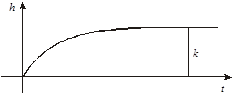
Рис. 3.9. Переходная характеристика

Импульсную переходную функцию (рис. 3.10) вычислим по соотношению

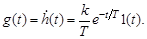(3.23)

Выражение, соответствующее амплитудно-фазовой характеристике апериодического звена, имеет вид

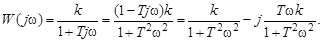(3.24)

По выражению

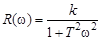(3.25)

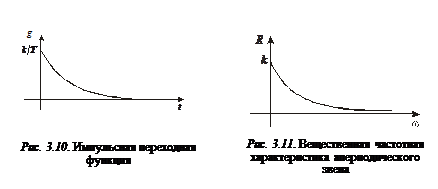
можно построить его вещественную частотную характеристику
(рис. 3.11).

Мнимая частотная характеристика (рис. 3.12) апериодического звена соответствует уравнению

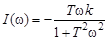. (3.26)

Рис. 3.12. Мнимая частотная характеристика
апериодического звена

Амплитудную частотную характеристику (рис. 3.13) описывает выражение

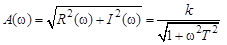. (3.27)

Фазовая частотная характеристика звена определяется соотношением

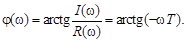(3.28)

Она представляет собой кривую (рис. 3.14) с пределом .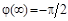

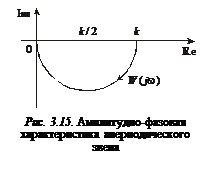
На комплексной плоскости по выражению (3.24) можно построить амплитудно-фазовую характеристику апериодического звена, которая имеет вид полуокружности (рис. 3.15).

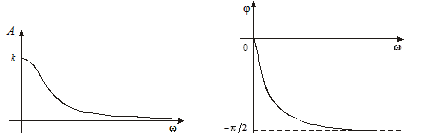
Рис. 3.13. АЧХ апериодического звена Рис. 3.14. ФЧХ апериодического звена

Запишем выражение для логарифмической амплитудной частотной характеристики

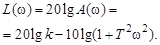(3.29)

Наиболее просто для звена можно построить асимптотичес-кую логарифмическую амплитудную частотную характеристику.
В этом случае следует рассмотреть отдельно области высоких и низких частот и для каждой определить свою асимптоту:

1) в области низких частот, когда 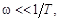вместо точной ЛАЧХ (3.29) можно рассмотреть приближенную

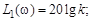(3.30)

2) в области высоких частот при 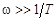вторая асимптота имеет вид

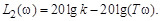(3.31)

На частоте 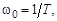которая называется собственной частотой апериодического звена, справедливо условие

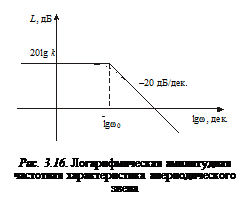
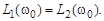
Точная характеристика звена на рис. 3.16 показана пунктирной линией и несколько отличается от асимптотической ЛАЧХ, причем наибольшая погрешность будет на собственной частоте .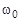

3.1.5. Форсирующее звено

Форсирующим называется звено, дифференциальное уравнение которого имеет вид

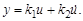(3.32)

Нетрудно убедиться в том, что (3.32) можно представить как сумму уравнений пропорционального и дифференцирующего звеньев.

Передаточную функцию форсирующего звена

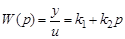
принято записывать в стандартной форме

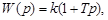(3.33)

где 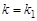– коэффициент усиления, а 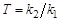– постоянная времени звена.

Передаточная функция (3.33) содержит полином в числителе, корень которого 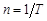называется «нулем» форсирующего звена.

Его переходная характеристика определяется соотношением

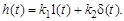(3.34)

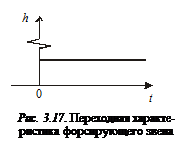Качественный вид ее приведен на рис. 3.17.

Импульсная переходная функция звена следующая:

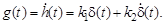(3.35)

Обобщенная частотная характеристика находится по передаточной функции (3.33) и имеет вид

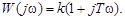(3.36)

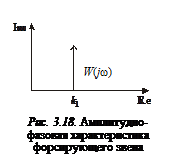Соответствующая амплитудно-фазовая характеристика изображена на рис. 3.18.

Вещественная частотная характеристика звена не зависит от частоты
и равна 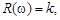мнимая частотная характеристика представляет собой прямую

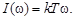
Амплитудная частотная характеристика может быть построена по выражению

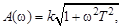
а фазовая частотная характеристика определяется в виде

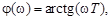(3.37)

причем в пределе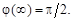

На основании выражения для 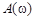определим логарифмическую амплитудную частотную характеристику

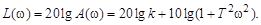(3.38)

Как и в предыдущем случае, для форсирующего звена удобнее строить не точную, а асимптотическую ЛАЧХ (рис. 3.19). Здесь 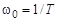– собственная частота звена.

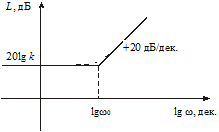
Рис. 3.19. Логарифмическая амплитудная
частотная характеристика форсирующего звена

Причем ее можно получить, исследуя отдельно области низких и высоких частот или суммируя ЛАЧХ пропорционального и дифференцирующего звеньев.

Нетрудно убедиться, сравнивая выражения (3.28) и (3.29)
с выражениями (3.37) и (3.38), в том, что логарифмические амплитудная и фазовая частотные характеристики форсирующего звена представляют собой зеркальное отображение относительно оси абсцисс соответствующих логарифмических характеристик апериодического звена.

3.1.6. Звено второго порядка

Дифференциальное уравнение звена второго порядка

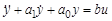(3.39)

принято записывать в стандартном виде

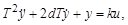(3.40)

где 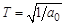– постоянная времени звена; d – коэффициент демпфирования, который определяет склонность переходных
процессов к колебаниям, 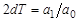; 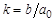– коэффициент
усиления.

Передаточную функцию звена получим на основе символической записи дифференциального уравнения

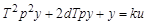
в виде

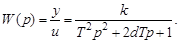(3.41)

Для определения модальных характеристик запишем характеристическое уравнение звена

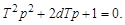(3.42)

Оно имеет два корня (полюса), которые в зависимости от коэффициента демпфирования d могут быть вещественными или комплексно-сопряженными, что приводит к различным переходным процессам. Рассмотрим варианты корней.

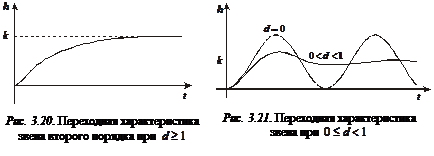
1. Если 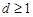, то корни уравнения (3.42) вещественные и положительные. Обозначим их через 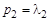и получим переходную функцию (рис. 3.20) в виде

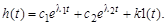(3.43)

2. Если 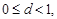то корни уравнения (3.42) будут комплексно-сопряженными, т. е.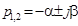 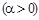. При 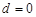получаем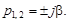

В случае, когда коэффициент демпфирования изменяется в диапазоне 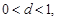звено второго порядка называют колебательным. Выражение для его переходной характеристики следующее:

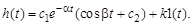(3.44)

Причем колебательность переходного процесса будет тем больше, чем меньше коэффициент демпфирования d. В пределе при 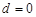будут иметь место незатухающие колебания. В этом случае звено называется консервативным. Соответствующие графики переход-ных процессов представлены на рис. 3.21.

Определим выражение для общей частотной характеристики колебательного звена, заменив p на 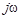в передаточной функции (3.41):

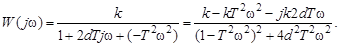(3.45)

Запишем выражения для вещественной частотной характе-
ристики

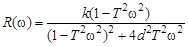(3.46)

и мнимой частотной характеристики:

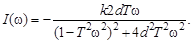(3.47)

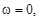
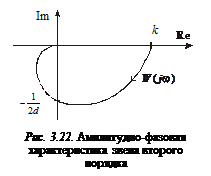
На основе (3.46) и (3.47) построим АЧХ на комплексной плоскости, рассматривая характерные точки: 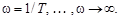Ее вид существенно зависит от коэффициента демпфирования d (рис. 3.22).

Амплитудно-фазовая характеристика консервативного звена 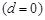начинается в точке k на вещественной оси и при увеличении 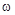стремится к 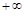, а затем из 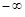– к началу координат.

Амплитудная частотная характеристика строится на основе выражения

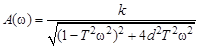(3.48)

и может иметь резонансный пик, высота которого будет тем больше, чем меньше коэффициент демпфирования d.

Формула для фазовой частотной характеристики имеет вид

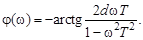(3.49)

Построение ЛАЧХ колебательного звена (при 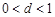) осуществляется по соотношению, полученному из (3.48):

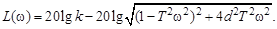(3.50)

При значениях коэффициента демпфирования в интервале 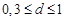можно строить упрощенную асимптотическую ЛАЧХ, рассматривая отдельно области высоких и низких частот.

В области низких частот 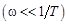асимптота имеет вид

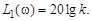
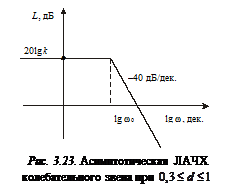В области высоких частот, когда получим вторую асимптоту (рис. 3.23)

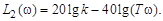
На собственной частоте колебательного звена 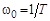справедливо соотношение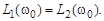

Наибольшее отличие асим-
птотической ЛАЧХ от дейст-
вительной характеристики на-
блюдается на частоте 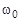(рис. 3.24) и зависит от величины коэф-
фициента демпфирования.

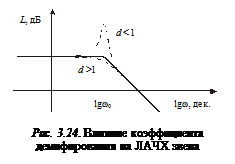При значениях 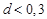не следует пользоваться асимптотической ЛАЧХ, а нужно строить точную логарифмическую характеристику.

При 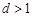корни характеристического уравнения (3.42) будут вещественными и передаточную функцию звена второго порядка (3.41) можно представить в виде произведения двух передаточных функций апериодических звеньев:

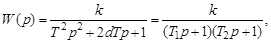(3.51)

где 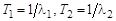– постоянные времени апериодических звеньев. В этом случае асимптотическая ЛАЧХ звена второго порядка имеет два «излома» на частотах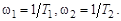

Она может быть получена суммированием асимптотических ЛАЧХ двух апериодических звеньев.

3.2. Структурные схемы

Структурной схемой будем называть графическую модель системы, в которой каждому элементу ставится в соответствие его динамическая характеристика. Такая схема наглядно отражает
состав системы и связи между отдельными ее составляющими.

При изображении структурной схемы будем придерживаться следующих обозначений ее элементов:

-

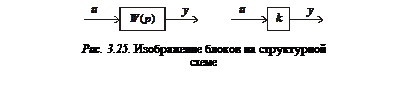блок с указанной внутри него динамической характеристикой элемента; входной и выходной сигналы блока обозначаются стрелками (рис. 3.25);

-

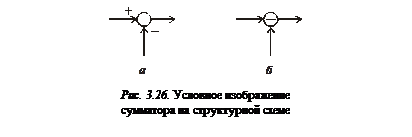сумматор (рис. 3.26), выход которого равен сумме входных сигналов. Знак каждого сигнала может быть указан возле соответствующего входа (рис. 3.26, а) или внутри сумматора; при этом знак «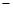» относится к перпендикулярно входящему сигналу
(рис. 3.26, б);

-

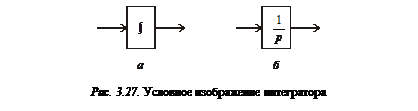интегратор на структурной схеме будем условно обозначать символом интегрирования (рис. 3.27, а) или в операторной форме (рис. 3.27, б);

Структурная схема может быть построена на основе как дифференциальных уравнений, так и передаточных функций.

Отметим, что переход от исходной передаточной функции или уравнения системы к ее структурной схеме может иметь несколько вариантов решения. Возможен и обратный переход, т. е. на основе структурной схемы можно получить дифференциальное уравнение системы, причем эта задача имеет единственное решение.

Рассмотрим вначале структурные схемы, которые получены с использованием передаточных функций. При таком представлении внутри блока указываются передаточная функция звена, а также входной и выходной сигналы (см. рис. 3.25). С целью упрощения структуры системы применяются различные ее преобразования, приведем основные из них.

3.3. Структурные преобразования

3.3.1. Последовательное соединение звеньев

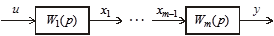Рассмотрим последовательное соединение типовых звеньев с передаточными функциями 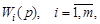и найдем выражение для общей передаточной функции, связывающей между собой входной и выходной сигналы системы (рис. 3.28).

Рис. 3.28. Последовательное соединение
m звеньев

Правило: передаточная функция последовательного соединения звеньев равна произведению передаточных функций всех звеньев, т. е.

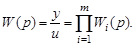(3.52)

В этом нетрудно убедиться, если выходную переменную системы представить в виде произведения передаточной функции звена и соответствующего входного сигнала

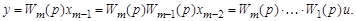
Отношение выходного сигнала системы y к ее входному сигналу u представляет собой общую передаточную функцию (3.52) соединения.

3.3.2. Параллельное соединение звеньев

Правило: передаточная функция параллельного соединения звеньев равна сумме передаточных функций отдельных звеньев:

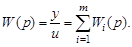(3.53)

Параллельное соединение звеньев показано на рис. 3.29.

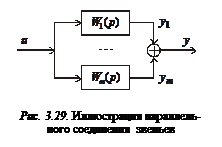Выходной сигнал системы представляет собой сумму выходных сигналов отдельных звеньев

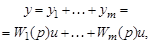
следовательно, общая передаточная функция параллельного соединения имеет вид (3.53).

3.3.3. Обратная связь

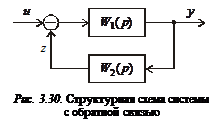Такое соединение звеньев показано на рис. 3.30, причем знак «–» внутри сумматора означает отрицательную обратную связь.