Операторный метод расчета переходных процессов в линейных цепях
Особенности расчета переходных процессов в цепях с некорректными начальными условиями
Этот метод основан на преобразовании Лапласа. Пусть f(t) – оригинал, а F(p) – изображение этого оригинала по Лапласу. Для сокращения применяют такие обозначения: f(t) F(p), F(p)=
F(p), F(p)=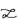
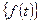
Прямое преобразование Лапласа определяется интегралом:
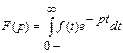 ,
, 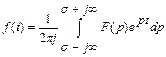
Для большого числа функций составлена таблица соответствия изображения и оригинала, кроме того, знание свойств преобразований Лапласа позволяет по небольшому числу выученных изображений находить широкий класс изображений функций.
Основными свойствами являются:
1. Свойство линейности
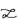
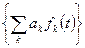 =
=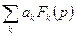 ,
, 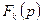

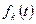 ,
,
2. 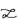
 ,
,
3. 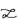
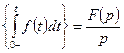 .
.
Последними двумя свойствами очень удобно решать дифференциальные уравнения.
Смещение аргумента:
- 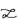
 ,
,
- 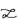
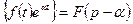 .
.
Свертка:
- 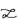
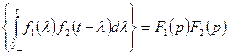 .
.
 2014-02-04
2014-02-04 674
674








